2. Аналитический подход к формированию информативной подсистемы признаков в задаче распознавания

Рассмотрим задачи формирования информативной подсистемы признаков в классической постановке. Пусть задана априорная информация в виде множества объектов X={x}, каждый из которых описан своим набором признаков x=(x¹, x², . . ., xⁿ). Предполагаем, что произведено разбиение объектов на непересекающиеся классы X₁,X₂,...,X_m и каждый класс X_P содержит k_P объектов, т.е.

Ставится следующая задача. Из исходной системы n признаков необходимо выделить подсистему из п' признаков (где п'<п), которая является наиболее информативной среди всех подсистем мощности п' в смысле наилучшего качества разбиения объектов на классы.

Предлагаемый ниже метод позволяет аналитически построить информативную подсистему признаков на примере одного вида функционала на основе максимизации которого в исходной системе из п признаков выбираются п' наиболее информативных признаков. Метод легко распространяется и на другие виды функционалов, например, на функционал, предложенный в. Следуя, введем необходимые понятия, которые будут использованы ниже. За меру близости, характеризующую среднеквадратичный разброс объектов классов X_p и X_q, будем использовать величину

.

В качестве меры близости между объектами данного класса X_P, p=1,2, . . ., m, примем величину

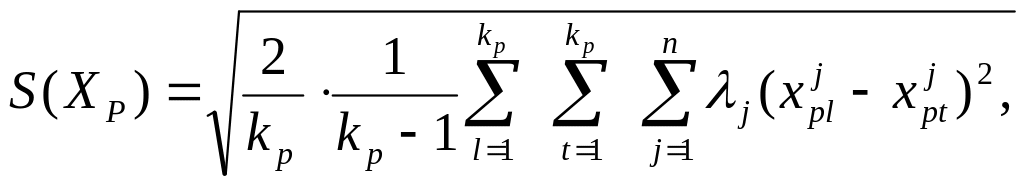
которая характеризует среднеквадратичный разброс объектов внутри класса Х_р.

Совокупность признаков объектов может быть описана n - мерным булевским вектором =(₁, ₂, . . ., _n), компоненты которого принимают значения 1 или 0 в зависимости от того, будет включен данный признак в информативную подсистему или нет.

Решим задачу определения информативной подсистемы признаков исходя из необходимости максимизации отношения расстояний между классами к среднеквадратичным разбросам объектов внутри классов. Формально это будет следующая задача максимина:

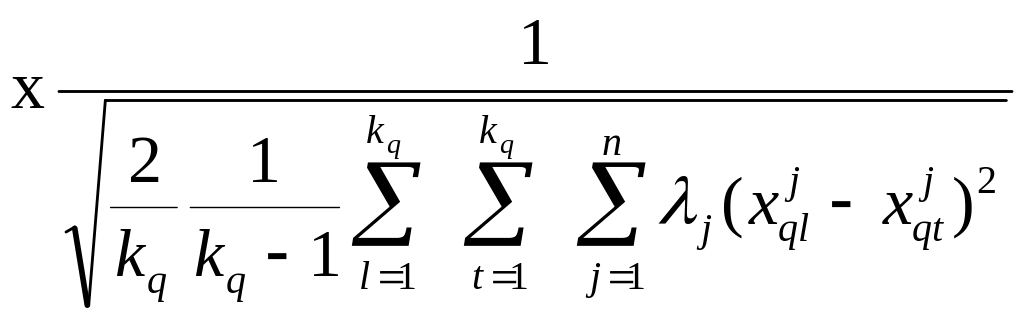. (1)

Введем обозначения:

(2)

Согласно (2) a_j, b_j, c_j, - положительные постоянные величины.

Для  имеем 0   < ½ .

Критерий информативности признаков, заданный в виде функционала задачи (1), является эвристическим и базируется на основополагающей в распознавании образов гипотезе компактности: с увеличением расстояния между классами улучшается их разделимость. Предпочтительными считаются те признаки, которые максимизируют это расстояние. В настоящем разделе для оценивания информативности признаков далее используются эвристические критерии, а именно - критерии, представленные функционалами вида

и

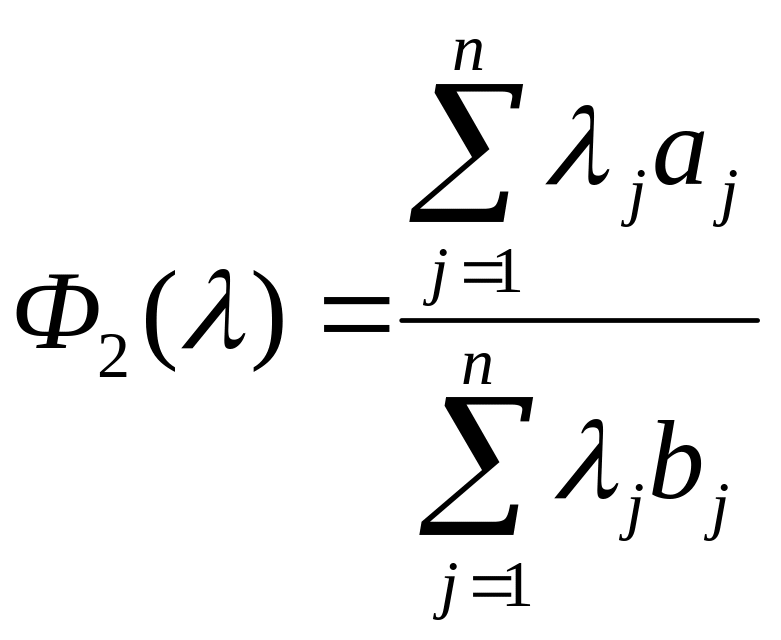
или функционалами сводимыми к этим видам, которые поддаются легко реализуемой максимизации. Выбор этих критериев обусловлен следующими обстоятельствами.

Известно, что наиболее обоснованным и естественным из всех критериев информативности признаков является оценка ошибки классификации, поставленная в соответствии всем наборам признаков, сформулированным на основе исходной системы переменных x=(x¹,x²,...,xⁿ). Преимущество такого определения критерия информативности состоит в том, что основанием служит задача распознавания: в результате выбора определенного набора признаков дается непосредственная количественная оценка информативности данного набора, связанная с качеством классификации. Однако реализация такого подхода к оцениванию информативности признаков требует выполнения значительного объема сложных вычислений.

Другая группа критериев, используемых для оценки качества признаков или их наборов, основана на статистике и теории информации. Эта группа включает критерии, основанные на мерах вероятностной зависимости. Результаты подробного анализа этих критериев приведены в, поэтому здесь отметим лишь, что все они, за исключением расстояния Бхаттачари, дивергенции, имеют сложный аналитический вид. Как отмечено в, большинство критериев этой группы в параметрическом виде использовать неудобно (их расчеты требуют многократного интегрирования), а в параметрическом – оценки вероятности ошибочной классификации получаются смещенными. Ввиду этого использование их для выбора информативных признаков весьма затруднено. Следовательно, возвращаясь к рассмотрению эвристических критериев, следует отметить, что они в отличие от критериев, основанных на статистике и теории информации, являются более простыми. Причем, несмотря на простоту, эвристические критерии в ряде случаев являются оптимальными. Именно эти особенности обусловили широкое применение их при решении практических задач классификации.

Справедлива следующая

Теорема 3.1. Пусть все множество объектов подразделено на классы Х₁,Х₂,...,Х_m, все классы априорно описаны на языке признаков X=(x¹,x²,...,xⁿ). Если априорная информация (2) ранжирована в виде

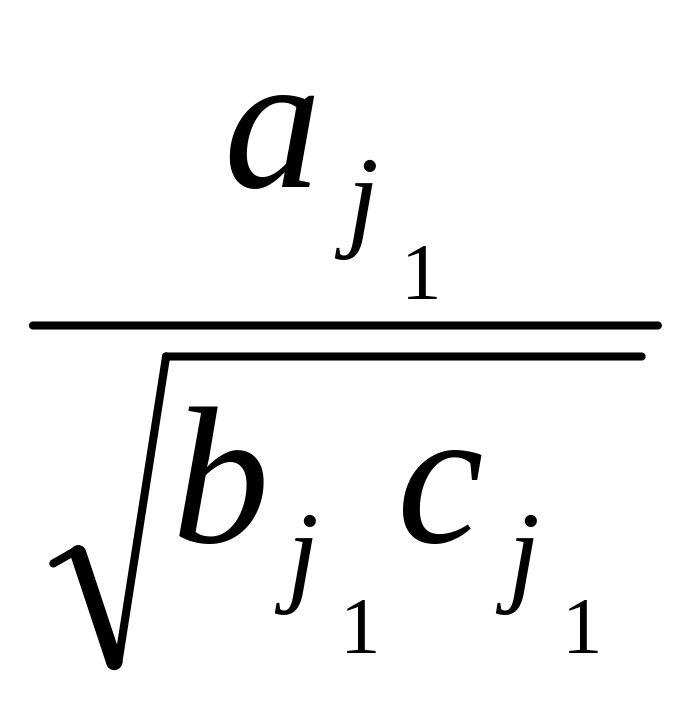
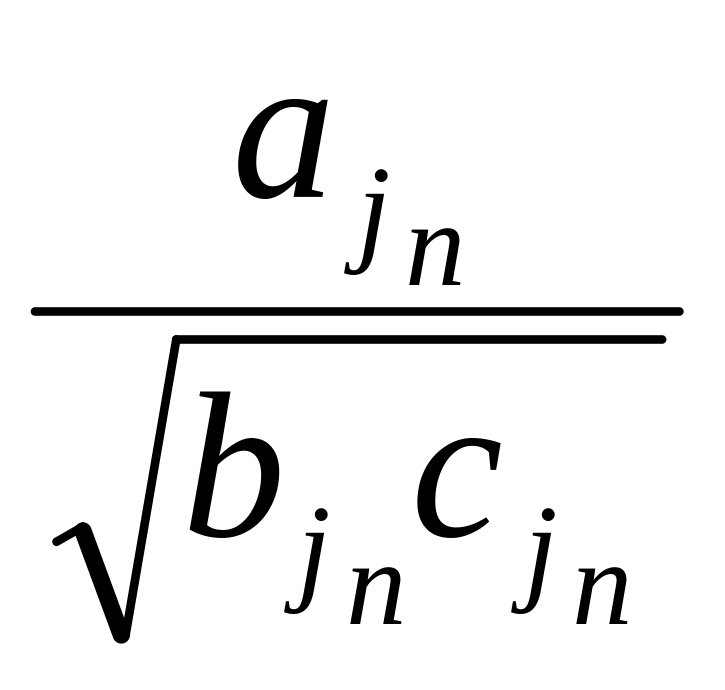 ... , (3)

то каждый набор информативной подсистемы из п' признаков формируется из первых п' признаков, соответствующих этой ранжированной последовательности.

Доказательство. Ограничим рассмотрение теоремы двумя классами, т.е. p=q=1 и далее, не нарушая общности рассуждений. Будем полагать _j=1(j=1,2,...,n), так как аналитическим способом выводится формула, на основе которой может быть определена информативная подсистема, состоящая из произвольного числа признаков п', где 1п'n. Полагая _j=1(j=1,2,...,n) и используя обозначения (2), функционал (1) перепишем следующим образом:

. (4)

Для знаменателя функционала (4) используем неравенство Гельдера. Неравенство Гельдера в общем случае имеет вид

где p>1; q=p/(p-1); x_{k ,}y_k 0 , (k=1,2,...,n).

Полагая p=2 и q=2/(2-1)=2, знаменатель функционала (1) представляем в виде

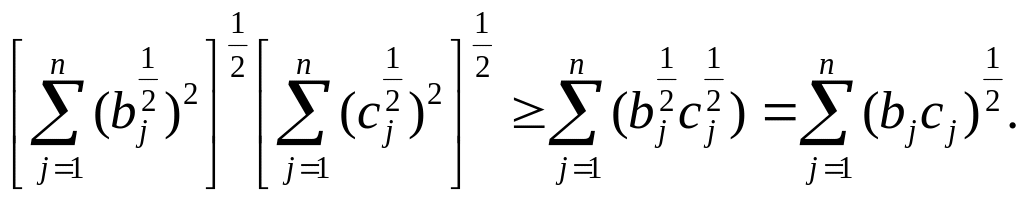(5)

Учитывая (5), выражение (4) записываем в виде:

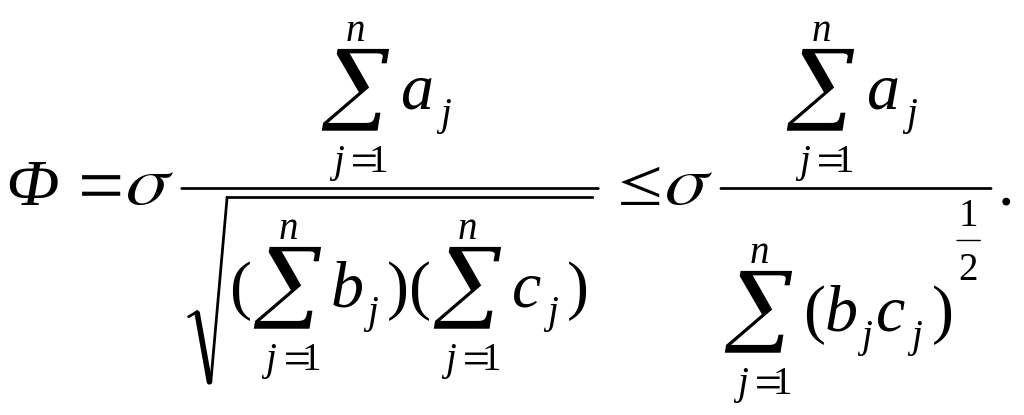(6)

Учитывая, что 0<1/2, из (6) получаем

. (7)

Последовательность величин a_j,b_j,c_j в (7) ранжируем следующим образом:

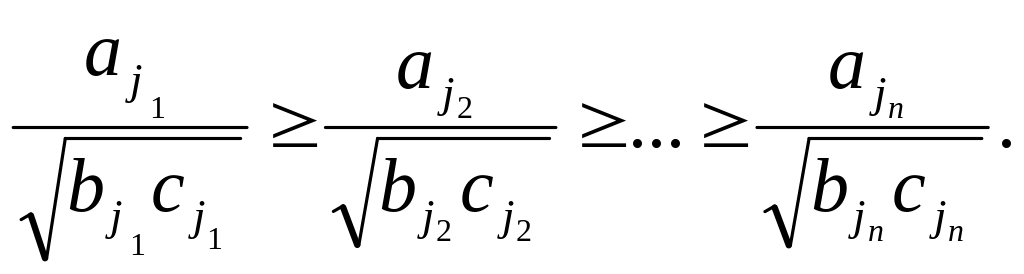
Тогда для положительных величин (j=1,2,3,...,n ) можно доказать справедливость неравенства

(8)

где 1  l₁  l₂  l₃  l₄  n .

Доказательство неравенства (8) приведено в разделе 3.3. Используя неравенство (8) для выражения (7), приходим к следующему результату:

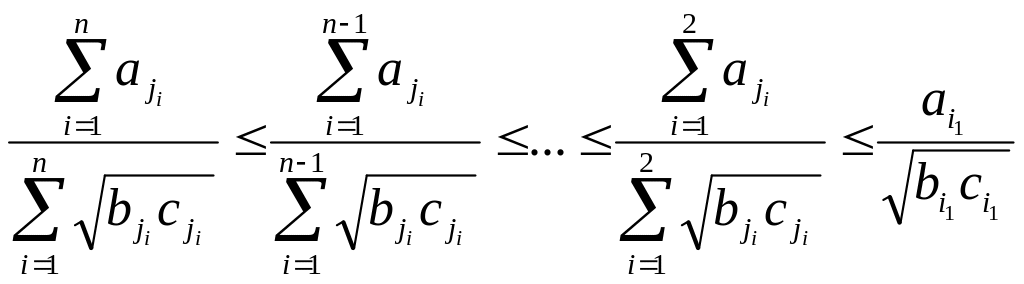(9)

С помощью соотношений (9) можно определить информативную подсистему, состоящую из произвольного числа признаков n' в пределах от 1 до n,

Теорема 2. Пусть имеется два набора информативных признаков и соответственно п' и п'' - числа признаков в каждом наборе, причем п'<п''. Тогда информативный признак, включенный в набор с числом признаков п', входит в набор с числом признаков n".

Если функционал (1) представим как функцию от числа выделенных информативных признаков n', т.е. Ф(п'), то справедлива следующая

Теорема 3. Если априорная информация (2) ранжирована в виде последовательности (3), то в зависимости от числа информативных признаков для функционала справедливо выражение

Ф(п'=1) Ф(п'=2)... Ф(п'=n)

Доказательства последних двух теорем непосредственно следуют из неравенств (9). Результаты, полученные для двух классов, обобщим для m классов.

Все пары из т классов можно перенумеровать, вводя индекс =1,2,..., ,где

.

Следовательно, для каждой пары из m классов можно записать свое выражение (9). При фиксированном п' выбираем тот набор признаков, для которого выражение

принимает наименьшее значение.

Сформулируем описанный здесь метод формирования информативной подсистемы признаков в виде алгоритма, обозначаемого далее как A₁.

Алгоритм А₁

Шаг 1. Вычисление значения функционала

для каждого исходного признака в отдельности.

Шаг 2. Ранжирование значений функционала, полученных на шаге 1, в виде последовательности неравенств (3).

Шаг 3. Формирование наиболее информативной подсистемы признаков заданной мощности п' из тех исходных признаков, которым соответствуют первые п' элементов ранжированной последовательности (3).