2. Марковские модели

Общие сведения. В теории массового обслуживания к наиболее изученным и исследованным относятся модели, у которых случайный процесс функционирования относится к классу марковских процессов, т. е. марковские модели.

Случайный процесс, протекающий в системе, называется марковским, если для любого момента времени вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент и не зависят от того, когда и как система пришла в это состояние.

При исследовании ВС аналитическим моделированием наибольшее значение имеют марковские случайные процессы с дискретными состояниями и непрерывным временем.

Процесс называется процессом с дискретными состояниями, если его возможные состояния z₁, z₂,... можно заранее перечислить, т. е. состояния системы принадлежат конечному множеству, и переход системы из одного состояния в другое происходит мгновенно.

Процесс называется процессом с непрерывным временем, если смена состояний может произойти в любой случайный момент.

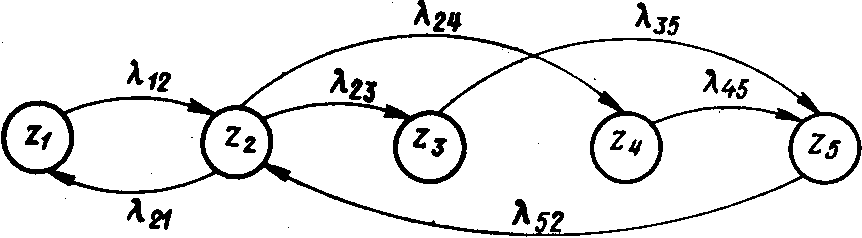
Рис. 3. Пример графа состояний

Описание марковской модели. Для описания поведения системы в виде марковской модели следует определить понятие состояния системы; выявить все состояния, в которых может находиться система; указать, в каком состояний находится система в начальный момент; построить граф состояний, т. е. изобразить все состояния, например, кружками и возможные переходы из состояния в состояние — стрелками, соединяющими состояния (на рис. 3 выделено пять состояний); разметить граф, т. е. для каждого перехода указать интенсивность потока событий, переводящих систему из состояния z_i в состояние z_j

(8)

где p_ij (t, t + — вероятность перехода из состояния z_i в состояние z_j за время от t до t + .

Для стационарных марковских процессов интенсивности переходов не зависят от времени: _ij (t) = _ij, тогда p_ij (t, t + .

Понятие состояния зависит от целей моделирования В одном случае, например, оно может быть определено по состояниям элементов, каждый из которых может быть "свободен" или "занят" в другом случае состояние системы определяется числом заявок, находящихся на обслуживании и в очередях.

Уравнения Колмогорова для вероятностей состояний. Исчерпывающей количественной характеристикой марковского процесса является совокупность вероятностей состояний, т. е. вероятностей p_i (t) того, что в момент t процесс будет находиться в состоянии z_i (t = 1, ..., n).

Рассмотрим, как определяются вероятности состояний по приведенному на рис. 3 графу состояний, считая все потоки простейшими. В случайный момент времени t система может находиться в одном из состояний z_i с вероятностью p_i (t). Придадим t малое приращение и найдем, например, p₂ (t + ) — вероятность того, что в момент t + t система будет в состоянии Z₂. Это может произойти, во-первых, если система в момент t была в состоянии Z₂ и за время не вышла из него; во-вторых, если в момент t система была в состоянии z₁ или z₂ и за время перешла в состояние Z₂.

В первом случае надо вероятность р₂(t) умножить на вероятность того, что за время система не перейдет в состояние z₁, z₂ или z₄. Суммарный поток событий, выводящий систему из состояния z₂, имеет интенсивность . Значит, вероятность того, что за время система выйдет из состояния z₂, равна . Отсюда вероятность первого варианта

Найдем вероятность перехода в состояние z₂. Если в момент t система находилась в состоянии z₁ с вероятностью p₁ (t), то вероятность перехода в состояние z₁ за время равна

Аналогично для состояния z₅

Складывая вероятности и , получим

,

Раскроем квадратные скобки, перенесем p₂ (t) в левую часть и разделим обечасти на :

.

Если устремить к нулю, то слева получим производную функции :

Аналогичные уравнения можно вывести для всех остальных состояний. Получается система дифференциальных уравнений:

(8)

Эта система линейных дифференциальных уравнений дает возможность найти вероятности состояний, если задать начальные условия. В левой части каждого уравнения стоит производная вероятности i-го состояния, а в правой — сумма произведений вероятностей всех состояний, из которых ведут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность i-гo состояния.

Представим уравнения Колмогорова в общем виде:

(9)

Здесь учтено, что для состояний, не имеющих непосредственных переходов, можно считать

Предельные вероятности состояний. В теории случайных процессов доказывается, что если число п состояний системы конечно и из каждого состояния можно перейти в любое другое за конечное число шагов, то существуют предельные (финальные) вероятности состояний:

(10)

Сумма вероятностей всех возможных состояний равна единице. При в системе S устанавливается стационарный режим, в ходе которого система случайным образом меняет свои состояния, но их вероятностные характеристики уже не зависят от времени. Предельную вероятность состояния z_i можно трактовать как среднее относительное время пребывания системы в этом состоянии.

Для вычисления предельных вероятностей нужно все левые части в уравнениях Колмогорова (9) положить равными нулю и решить полученную систему линейных алгебраических уравнений:

(11)

В связи с тем, что эти уравнения однородные, т. е. не имеют свободного члена и, значит, позволяют определить неизвестные только с точностью до произвольного множителя, следует восполь­зоваться нормировочным условием

(12)

и с его помощью решить систему уравнений.

Модель размножения и гибели. Разновидностью марковской модели с дискретным числом состояний и непрерывным временем является модель размножения и гибели. Она характерна тем, что ее граф состояний имеет вид цепи (рис. 4). Особенность этого графа состоит в том, что каждое из средних состояний z₁, ..., z_n-1 связано прямой и обратной стрелками с каждым из соседних состояний — п z_j равым и левым, а крайние состояния z₀ и z_n — только с одним соседним состоянием.

λ_0,1 λ_1,2

z₀ z₁

^λ_0,1 ^λ_1,2

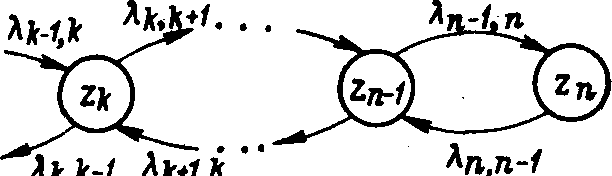
Рис. 4. Граф состояний модели размножения и гибели

В этой модели формулы для определения вероятностей состояний, полученные в результате решения уравнений Колмогорова, имеют вид:

(13)

(14)

Эти формулы часто, используют при решении задач теории массового обслуживания.

Контрольные вопросы

1. Простейший поток и его свойства.

2. Основная характеристика экспоненциального распределения.

3. Пуассоновский поток.

4. Поток Эрланга и его основные свойства.

5. Какой процесс называется Марковским описание Марковской модели?

6. Для чего используется уравнение Колмогорова?

7. Граф состояний модели размножения и гибели и основные формулы.

Литература

Лекция 10. ХАРАКТЕРИСТИКИ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ (2 часа)

План

1. Характеристики вычислительных систем как систем массового обслуживания

2. Характеристики вычислительных систем как сложных систем массового обслуживания

3. Методы приближённой оценки характеристик вычислительных систем

1. Характеристики вычислительных систем как систем массового обслуживания

Описание системы. Предположим, что моделью ВС является одноканальная СМО с однородным бесконечным простейшим потоком заявок и неограниченной очередью. Интенсивность потока заявок равна . Длительность обслуживания заявки — это случайная величина с математическим ожиданием .

Наряду с понятием средней длительности обслуживания используется понятие интенсивности обслуживания — величины, обратной , и характеризующей число заявок, которое может обслужить прибор в единицу времени.

Поток обслуживания тоже будем считать простейшим с интенсивностью . В соответствии с символикой, принятой в теории массового обслуживания, такая система обозначается М/М/1.

Выделим состояния СМО по числу заявок, находящихся в системе:

z₀ — прибор свободен, очереди нет;

z₁ — прибор занят (обслуживает заявку), очереди нет;

z₂ — прибор занят, одна заявка в очереди;

z_k — прибор занят, (k — 1) заявок стоит в очереди.

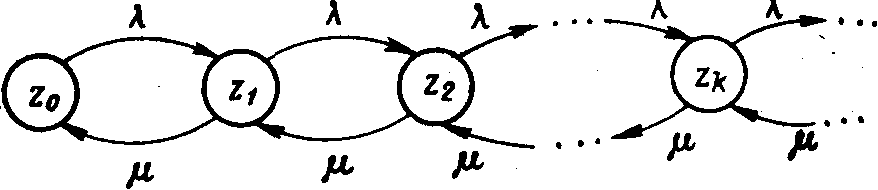
Рис. 5. Граф состояний СМО

Граф состояний такой системы изображен на рис. 5. Это модель размножения и гибели, но с бесконечным количеством состояний, поскольку, очередь неограниченна.

Коэффициент загрузки. Предельная вероятность состояния

(1)

Обозначая получаем

. (2)

Ряд в этой формуле представляет собой геометрическую прогрессию. Известно, что при ρ < 1 ряд сходится. Сумма членов прогрессии при этом равна 1/(1 — ρ), откуда

Это вероятность того, что прибор свободен и очередь отсутствует. Значит, вероятность того, что прибор занят обслуживанием заявки,

Это означает, что отношение

(3)

служит мерой загрузки СМО и является коэффициентом загрузки. Тогда коэффициент простоя.

Число заявок в СМО. Вероятности состояний z₁, ..., z_k, ... определяются из общей формулы размножения и гибели:

Определим среднее число заявок в системе п. В текущий момент времени в системе может быть 0, 1, 2, .... k, ... заявок с вероятностями p₀, p₁, p₂,…, p_k… Математическое ожида­ние количества заявок равно

Подставим значение р_k и р₀, исключив первое слагаемое, равное нулю:

Вынесем за знак суммы ρ (1 — р):

Но — это производная по от :

.

Меняя местами операции дифференцирования и суммирования, получим

(4)

Сумма в этой формуле — это сумма бесконечно убывающей прогрессии при она равна ρ/(1—ρ), а ее производная 1/(1- ρ)². Следовательно, число заявок в системе в установившемся стационарном режиме

п = ρ/(1 - р). (5)

Длина очереди. Найдем среднее число заявок в очереди к обслуживающему прибору — среднюю длину очереди l. Она равна среднему числу заявок в системе за вычетом среднего числа заявок, находящихся под обслуживанием. Число заявок под обслуживанием может быть равно нулю, если прибор свободен, или единице, если прибор занят. В установившемся режиме математическое ожидание такой случайной величины равно вероятности того, что прибор занят. А эта вероятность определена ранее — р. Откуда получается средняя длина очереди в СМО:

(6)

Зависимость средней длины очереди от коэффициента загрузки изображена на рис. 2. При ρ > 0,6—0,7 очередь стремительно увеличивается и при ρ 1 уходит в бесконечность. У детерминированной системы коэффициенты вариации интенсивностей потоков заявок и обслуживания равны нулю, при ρ < 1 очередь отсутствует, а при ρ 1 — уходит в бесконечность. Для систем, которые имеют промежуточные коэффициенты вариации 0 <v < 1, зависимости средней длины очереди от коэффициента загрузки лежат в области, заштрихованной на рис. 2.

Время реакции. Для определения среднего времени реакции рассмотрим поток заявок, прибывающих в СМО, и поток заявок, покидающих систему. Если в системе устанавливается предельный стационарный режим при ρ<1, то среднее число заявок, прибывающих в единицу времени, равно среднему числу заявок, покидающих ее: оба потока имеют интенсивность .

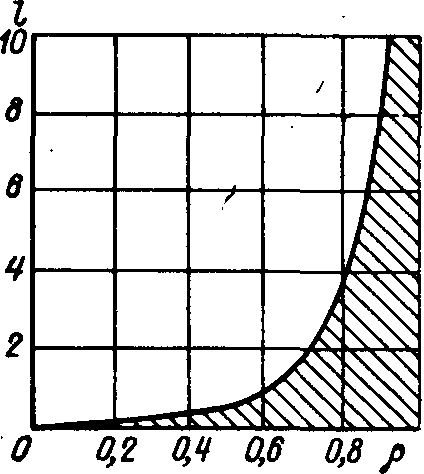
Рис. 2. Зависимость средней длины очереди от коэффициента загрузки для простейшей СМО

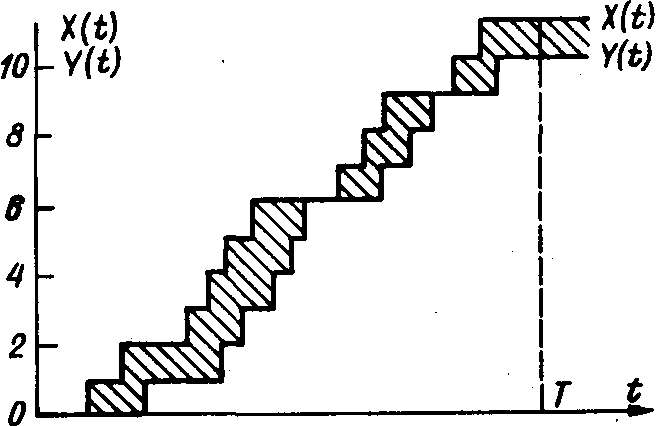
Рис. 3. Временная диаграмма процессов поступления и ухода заявок

Обозначим через Х (t) число заявок, поступивших в СМО до момента времени t, а через Y (t) — число заявок, покинувших СМО до момента t. Та и. другая функции являются случайными и меняются скачком — увеличиваются на единицу в моменты прихода или ухода заявок (рис. 3).

Очевидно, что для любого момента времени t разность функций п (t)=Х (t) — Y (t) есть число заявок, находящихся в СМО. Рассмотрим большой промежуток времени Т и вычислим среднее число заявок, находящихся в системе:

Интеграл изображен в виде заштрихованной фигуры на рис. 3. Она состоит из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе i-й заявки t_i:

где сумма распространяется на все заявки, поступившие в систему за время Т.

Разделим правую и левую части на Т.

Разделим и умножим правую часть на :

Произведение ,—это среднее количество заявок, пришедших за время Т. Если разделить сумму всех времен t_i на среднее число заявок, то получится среднее время пребывания заявки в системе, т. е. среднее время реакции и:

(7)

Это формула Литтла: для каждой СМО при любом характере потока заявок и при любом распределении времени обслуживания среднее время реакции равняется среднему числу заявок в системе, деленному на интенсивность потока заявок. Отсюда получается:

(8)

Вторая формула Литтла связывает среднее время пребывания заявки в очереди и среднее число заявок в очереди подобным соотношением:

(9)

Среднее время реакции равняется сумме среднего времени пребывания заявки в очереди и средней длительности обслуживания заявки:

(10)

Важно отметить, что в системе М/М/ 1 времена ожидания и реакции, а также периоды между моментами ухода следующих друг за другом заявок распределены по экспоненциальному закону. Для других систем при аналитическом моделировании не всегда представляется возможным определить законы распределения выходных характеристик.

При ρ > 1 в системе не устанавливается стационарный режим. В пределе длина очереди, а значит, и времена ожидания и реакции стремятся к бесконечности.