3. Методы генерации случайных величин и последовательностей

Датчики равномерно распределенных случайных чисел. При ста­тистическом моделировании стохастических систем возникает не­обходимость в определении случайных событий, величин и после­довательностей по заданным статистическим характеристикам. В основе их определения лежит использование последовательности чисел, равномерно распределенных в интервале (0,1). Программы ВС, формирующие такие последовательности, называют датчиками или генераторами случайных чисел.

Для получения последовательности равномерно распределен­ных случайных чисел с помощью ВС часто используется мульти­пликативный способ. Случайные числа получаются из рекуррент­ного соотношения

(17)

где А, С — константы; М — достаточно большое положительное целое число.

При соответствующем выборе констант и задании некоторого начального значения эта формула позволяет получать после­довательность целых чисел, равномерно распределенных в ин­тервале (0, М — 1). Последовательность имеет период повторе­ния, равный М. Поэтому точнее называть числа псевдослучай­ными. Случайные числа, равномерно распределенные в интервале (0,1), находятся масштабным преобразованием полученных целых чисел.

Моделирование случайных событий и дискретных величин. Для моделирования случайного события X, наступающего с ве­роятностью Р, берется значение случайного числа, равномерно распределенного на интервале (0,1), и сравнивается с Р. Если Р, то считается, что произошло событие X.

Предположим, что дискретная случайная величина Y может принимать значения y₁, …, y_n вероятностями р₁, ..., р_п.. При этом

.

Тогда берется значение случайного числа, распределенного равномерно на интервале (0, 1), и определяется такое k, принад­лежащее совокупности (1, n), при котором удовлетворяется не­равенство

Тогда случайная величина Y принимает значение у_k..

Моделирование случайных непрерывных величин. Пусть непре­рывная случайная величина Y имеет произвольный закон распре­деления. Предположим, что она задается эмпирической плот­ностью распределения f* (у) — гистограммой (рис. 5, а). Из гистограммы определяется эмпирическая функция распределения F* (у) — дискретная кумулятивная функция (рис. 5, б) для сере­дин интервалов группирования случайной величины в пределах (y_min, y _max).

Для определения одного конкретного значения случайной величины Y берется значение α случайного числа, равномерно распределенного на интервале (0, 1). Затем находится такое k, при котором

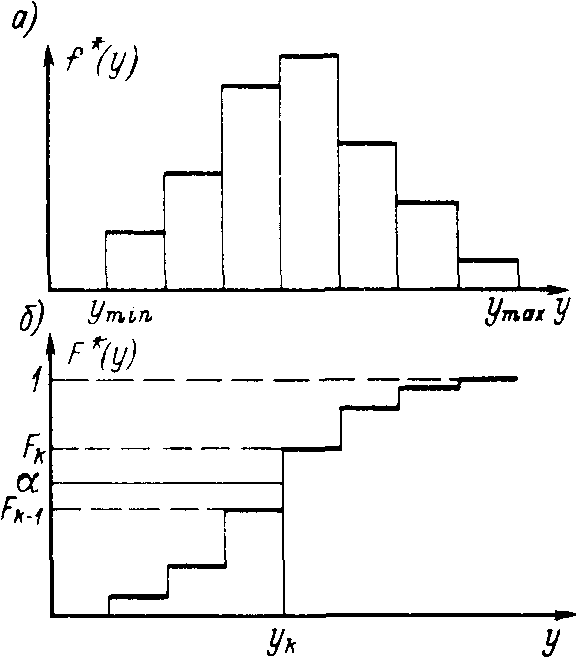
Рис. 5. Графики для определения значе­ния случайного числа по дискретной и интегральной функции распределения

Тогда искомое случайное число равное (рис. 5, б). Это же правило применимо и при задании случайной непрерывной вели­чины интегральной функцией распределения F (у), как показано на рис. 5, б. Оно вытекает из теоремы: если случайная вели­чина Y имеет плотность распределения F (у), то ее распределение

(18)

является равномерным на интервале (0, 1).

Для некоторых законов распределения (экспоненциальный, Эрланга) имеются простые аналитические зависимости у = Ф ( ). Например, пусть требуется получить конкретное значение слу­чайного числа Y с экспоненциальным законом распределения. Подставим в формулу (18) а и плотность распределения:

После интегрирования получается

Разрешая это уравнение относительно у_k,, имеем

Учитывая, что если случайная величина подчинена равно­мерному закону распределения в интервале (0, 1), то случайная величина также имеет равномерный закон распре­деления в интервале (0, 1), последнее соотношение можно заме­нить следующим:

(19)

Процедура определения конкретного значения случайного числа с заданным законом распределения называется случайным испытанием или «бросанием жребия».

Моделирование случайных процессов сводится на практике к определению последовательностей случайных величин. Исход­ными данными являются функции распределения, определенные в требуемые моменты времени, и последовательность случайных чисел подчиняющаяся равномерному закону распре­деления в интервале (0, 1). Конкретные значения случайных процессов в нужные моменты времени находят по изложенным выше правилам.

В большом числе публикаций, рассматриваются вопросы алгоритмизации, программирования и исследования качества датчиков случайных чисел.

В процессе статистического моделирования существует необ­ходимость в частом обращении к датчикам случайных чисел. С их помощью формируются конкретные значения случайных параметров каждой заявки, параметров обслуживания заявки каждым устройством; определяются пути продвижения заявки по тому или иному маршруту при вероятностной дисциплине маршрутизации и т. д. Имитационное моделирование систем по принципу особых состояний проводится с постоянным ис­пользованием датчиков случайных чисел для формирования всех управляющих последовательностей.