17. Числовые характеристики системы двух св. Корреляционный момент. Коэффицент корреляции.

Математическое ожидание двумерных СВ:

Пусть (X,Y) – двумерная СВ, тогда M(X,Y)=(M(X), M(Y)), т.е. матожидание случайного вектора – это вектор из матожиданий компонент вектора.

Если (X,Y) - дискретный случайный вектор с распределением (таблица в вопр. 16), то матожидания вычисляются по формулам:

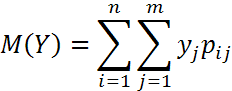
Для непрерывных СВ:

Если p(x,y) – совместная плотность распределения непрерывной двумерной СВ

Дисперсия двумерных СВ:

Корни квадратные из дисперсии называют средними квадратичными отклонениями

Начальным моментом порядка k,s системы (х,у) называется матожидание произведения x^k * y^s α_ks= M[ ^k * ^s]

Центральным моментом порядка k,s системы (х,у) называется матожидание произведения центрированных СВ

и – центрированные величины; m_х – матожидание

Начальный и центральный моменты для дискретных СВ:

, где p_ij = P(X=x_i ; Y=y_j)

Замечание:

k+s = 1 (1;0) => α_1;0 = M[xy⁰] = M[x] = m_x

(0;1) => α_0;1 = M[y] = M[y] = m_y

k+s = 2 (2;0) => µ_2;0 = M[ ⁰] = M[ ²] = D(X)

(1;1) => µ_0;1 = M[ * ] = k_xy

(0;2) => µ_0;2 = M[ ²] = D(Y)

Корреляционный момент k_xy = cov(x,y), хар-т рассеивание СВ и связь между ними (величина размерная) k_xy = M[x;y] – m[x]*m[y]

Коэффициент корреляции (величина безразмерная): R_xy =

Если x,y – независимы, то R_x,y = 0.

Величины, для которых R_x,y = 0 – некоррелированные.

Коэффициент корреляции характеризует линейную зависимость, т.е. при росте одной СВ другая имеет тенденцию изменяться по линейному закону.

Если х и у связаны точной (функциональной) зависимостью, то У=аХ+b. Если это так, то если а>0, R_xy =1 и а<0, R_xy= -1

В остальных случаях (нелинейно зависимые) – комби. (-1;1)

18. Теоремы о числовых хар-ках, их применение.

Пусть даны 2 СВ Х и У и известны M[x] и M[y],σ_x и σ_y

1. Матожидание СВ С равно самой этой величине. M[C] = C

Пусть Х – дискретная, (х=С, p=1), тогда M[C] = xp = 1*C = C

2. Дисперсия неслучайной величины С=0

D[C] = M[(C – M[C])²] = 0

3. Вынесение неслучайной величины за знак мат. ожидания

M[CX] = C*M[X]

4. Вынесение неслучайной величины за знак дисперсии и СДО

D[CX] = C²*D[X] σ[CX] = |C|*σ[X]

5. Матожидание суммы случайных величин (независимо от того, зависимы они или нет) M[X+Y] = M[X] + M[Y]

6. Матожидание линейной функции

M[aХ + bY + c] = aM[X] + bM[Y] + c

7. Дисперсия суммы случайных величин

D[X+Y] = D[X] + D[Y] – 2k_xy

Если х,у некоррелированы, то k_xy=0, тогда

D[X+Y] = D[X] + D[Y]

8. Дисперсия линейной функции

D[aX + bY + c] = a²D[X] + b²D[Y] – 2ab* k_xy

k_xy = M[XY] – m[x]*m[y] – корреляционный момент

9. Матожидание произведения СВ

M[XY] = M[X] * M[Y] + k_xy

10. Дисперсия произведения независимых СВ

D[XY] = D[X] * D[Y] + M[X]² * D[Y] + M[Y]² * D[X]

Для центрированных (M[X]=M[Y]=0) – D[ ] = D[ ] * D[ ]

Применение теорем:

1) Доказать, что СВ связаны линейной функциональной зависимостью Y=aX+b

2) Определить М(Х) числа появлений события при нескольких опытах

3) Найти дисперсию числа появлений события при нескольких независимых и зависимых опытах

4) Средний расход средств до достижения числа опытов до k-го появления события

(M(X)=ΣM(X_i)=k/p, D(X)=ΣD(X_i)=kq/p², σ=(√kq)/p