27. Проверка статистических гипотез. Гипотеза о неизвестном среднем при известной дисперсии на примере нормального распределения.

Проверка статистических гипотез – см. вопрос 26.

Проверка статистической гипотезы о матожидании нормального распределения при известной дисперсии

Пусть имеется нормально распределенная СВ . D =  ². Матожидание M неизвестно. Допустим, что M = a, где a – некоторое число. Будем считать также, что имеется другая информация, указывающая на то, что M = a₁, где a₁ > a.

Выдвигаем нулевую гипотезу H₀:M=a; при конкурирующей гипотезе H₁:M=a₁

Делаем выборку объема n: x₁, x₂,..., x_n . В основе проверки лежит тот факт, что СВ (выборочная средняя) распределена по нормальному закону с дисперсией ²/n и математическим ожиданием, равным a в случае справедливости H₀, и равным a₁ в случае справедливости H₁.

В качестве статистического критерия выбирается случайная величина z=( -a)(√n)/σ, распределенная по нормальному закону.

По принятому уровню значимости (ошибка 1 рода)  (например  = 0,05), используя то, что случайная величина z имеет НЗР, определим значение K_кр :

 = P(K_кр < z <) = () – (K_кр) = 0,5 – (K_кр).

Отсюда, Ф(K_кр)=(1–2)/ и осталось воспользоваться таблицей функции Лапласа для нахождения числа K_кр.

Если величина z, полученная при выборочном значении , попадает в область принятия гипотезы (z < K_кр), то гипотеза H₀ принимается. Если величина z попадает в критическую область, то гипотеза H₀ отвергается.

Если в задаче поставить другое условие: H₀:M = a; H₁: M = a₁ , a₁ < a, то критическая область здесь левосторонняя.

Рассмотрим теперь такую задачу: H₀: M=a; H₁: Ma.

В данном случае большие отклонения величины z от нуля в положительную или отрицательную сторону должны приводить к заключению о ложности гипотезы H₀, то есть здесь следует рассматривать двустороннюю критическую область. Критическое значение K_кр определяется с помощью соотношения P(K_кр<z<K_кр) =1–=(K_кр)–(–K_кр)=2(K_кр). Из этого соотношения следует: (K_кр)= (1–)/.

Нулевая Г.	Предположения	Статистика критерия	Альтернативная гипотеза	Критерий отклонения гипотезы
a=a0	σ2 неизвестна	t=(x-a0)*√n/σ	a=a1>a0 a=a1<a0	|t|>t1-2α
			a=a1≠a0	|t|>t1-α
a=a0	σ2 известна	t=(x-a0)*(√n-1)/σ	a=a1>a0 a=a1<a0	|t|>t1-2α, n-1
			a=a1≠a0	|t|>t1-α, n-1

28. Важнейшие распределения в математической статистике: распределение хи-квадрат, распределение Стьюдента.

Распределение χ2 (хи-квадрат) с n степенями свободы — это распределение суммы квадратов n независимых стандартных нормальных СВ.

Пусть U_k, – набор из n независимых нормально распределенных СВ, U_k~N(0;1). Тогда СВ имеет распределение хи-квадрат (χ²-распределение) с n степенями свободы, что обозначается как X_n~χ²(n).

Свойства распределения хи-квадрат:

1) СВ X_n имеет следующую плотность распределения:

, где – гамма-функция. Графики функций f(x,n), называемые кривыми Пирсона, ассиметричны и начиная с n>2 имеют один максимум в точке x=n-2:

2) Характеристическая функция СВ X_n имеет вид

3) СВ X_n имеет следующие моменты: М(X_n)=n, D(X_n)=2n.

4) Сумма любого числа m независимых СВ X_k, , имеющих распределение хи-квадрат с n_k степенями свободы, имеет распределение хи-квадрат с степенями свободы.

5) Распределение хи-квадрат обладает свойством асимптотической нормальности: , где СВ U имеет распределение N(0;1). Это означает, что при достаточно большом объеме n выборки можно приближенно считать X_n~N(n;2n). Фактически эта аппроксимация имеет место уже при n≥30.

Распределение Стьюдента

Распределение Стьюдента – это однопараметрическое семейство абсолютно непрерывных распределений.

Пусть U и X_n - независимые СВ, U~N(0;1), X_n~χ²(n). Тогда СВ T_n=U/(√X_n/n) имеет распределение Стьюдента с n степенями свободы, что обозначают как T_n~S(n).

Свойства распределения Стьюдента:

1) СВ T_n имеет плотность распределения

Графики плотностей f(t,n), называемые кривыми Стьюдента, симметричны при всех n=1,2,… относительно оси ординат:

2) СВ T_n имеет матожидание, равное M(T_n)=0 для всех n≥2, и дисперсию D(T_n)=n/(n-2) при n>2. При n=2 дисперсия D(T_n)=+∞.

3) При n→∞ распределение S(n) асимптотически нормально, т.е. T_n→U, где СВ U имеет распределение N(0;1). При n≥30 распределение С. S(n) практически не отличается от N(0;1).

Распределение χ2 (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.

Пусть X₁….Х_k совместно независимые стандартные нормальные случайные величины, то есть:

Тогда случайная величина имеет распределение хи-квадрат с k степенями свободы, обозначаемое

З амечание. Распределение хи-квадрат является частным случаем Гамма распределения:

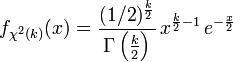
Следовательно, плотность распределения хи-квадрат имеет вид

а его функция распределения

Плотность вероятности: Функция распределения

Распределение Стьюдента

Распределение Стьюдента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений.

Пусть Y₀ ,Y₁, ………Y_n независимые стандартные нормальные случайные величины, такие что

Тогда распределение случайной величины t, где называется распределением Стьюдента с n степенями свободы. Пишут Её распределение абсолютно непрерывно и имеет плотность где — гамма-функция Эйлера.

Свойства распределения Стьюдента

Распределение Стьюдента симметрично. В частности если то

Плотность вероятности: Функция распределения: