6. Повторение независимых испытаний. Схема Бернулли. Формула Бернулли.

На практике часто приходится встречаться с задачами, в которых один и тот же опыт или аналогичные опыты повторяются неоднократно. В результате каждого такого опыта может появиться или не появиться событие А. Нас будет интересовать не исход отдельно взятого опыта, а всей серии опытов, а именно сколько раз произошло событий А. Мы должны найти вероятности произвольного числа появлений события А. опыты не зависимы.

Примеры: подбрасывание монеты, стрельба по мишени и т.д.

Опыты могут производиться в одинаковых или различных условиях, в связи с этим существуют 2 теоремы – частная и общая.

Частная теорема о повторении опытов:

Число всех комбинаций равно числу способов выбора из n испытании m, в которых событие A произошло, т.е. числу сочетаний С_n^m. Вероятность каждой такой комбинации (каждого варианта появления события B_m) по теореме умножения для независимых событий равна p^mq^n-m. В связи с тем, что комбинации между собой несовместны, по теореме сложения вероятностей получим: P(B)=P_m,n=С_n^mp^mq^n-m. (формула Бернулли)

Распределение вероятности по такому закону носит название биноминального распределения.

Общая теорема о повторении опытов:

Вероятность того, что событие А в n-независимых опытах появится m раз равна коэффициенту при Z^m в выражении:

Под схемой Бернулли понимают конечную серию n повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают p, а непоявления его q=1-p.

Вероятность того, что событие А в этих n-независимых испытаниях появится ровно m раз, выражается формулой Бернулли.

То значение m₀, при котором число P_m,n является max из множества {P_m,n}, называется наивероятнейшим, и оно удовлетворяет условию np-q ≤ m₀ ≤ np+p

При достаточно большой серии испытаний формула Бернулли становится трудно применимой, и в этих случаях используют приближенные формулы. Одну из них можно получить из предельной теоремы Пуассона:

, где 𝜆=np.

Пример. Вероятность изготовления на станке стандартной детали равна 0,8. Найти вероятности возможного числа появления бракованных деталей среди пяти отобранных.

Р_0,5= С₅⁰0,2⁰0,8⁵. Р_1,5. Р_2,5. Р_3,5. Р_4,5. Р_5,5.

Полученные вероятности изобразим графически точками с координатами (m, P_m,n). Соединяя эти точки, получим многоугольник, или полигон, распределения вероятностей.

7. Дискретная случайная величина. Ряд распределения. Функция распределения.

СВ – величина, которая в результате опыта может принять то или иное значение, неизвестное заранее какое именно. Обозначается X=f(ω), где ω – элементарный исход.

Для дискретной CВ множество возможных значений СВ, т.е. функции f(ω), конечно или счетно. Например, кол-во появлений герба при подбрасывании 3 раз монеты {0,1,2,3}.

СВ обозначаются прописными буквами латинского алфавита X, Y, Z, а их значения – соотв-щим строчным буквам x, y, z.

Ряд распределения СВ – закон распределения дискретной СВ:	х	1	2	…	n
	р	p1	p2	…	pn

Законом распределения СВ называется любое соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.

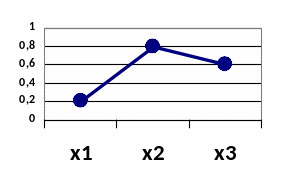
Ряд распределения можно представить графически (соединение полученных точек образует ломаную, называемую многоугольником распределения вероятностей:

С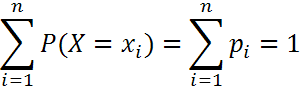 обытия Х=х₁, Х=х₂, …, Х=х_n, состоящие в том, что в результате испытания СВ Х примет соответственно значения х₁, х₂, …, х_n, являются несовместными и единственно возможными (ибо в таблице перечислены все возможные значения СВ), т.е. образуют полную группу. След., сумма их вероятностей равна 1. Для любой дискретной СВ:

Однако закон распределения СВ не является единственным и не универсально. Так, оно не применимо для непрерывной СВ, т.к., в первую очередь, потому что нельзя перечислить все бесконечное несчетное множ-во ее значений.

Для описания закона распределения СВ Х возможен и другой подход: рассматривать не вероятности событий Х=х для разных х (как это имеет место в ряде распределения), а вероятности события Х<х, где х – текущая переменная. Вероятность Р(Х<х), очевидно, зависит от х, т.е. является некоторой функцией от х.

Функцией распределения СВ X называется функция F(x), выражающая для каждого х вероятность того, что СВ X примет значение, меньшее х: F(x)= Р(Х<х).

Пример:

Х:	xi	1	4	5	7
	pi	0.4	0.1	0.3	0.2

F(x)=		0 при х≤1
		0,4 при 1<x≤4
		0,5 при 4<x≤5
		0,8 при 5<x≤7
		1 при x>7

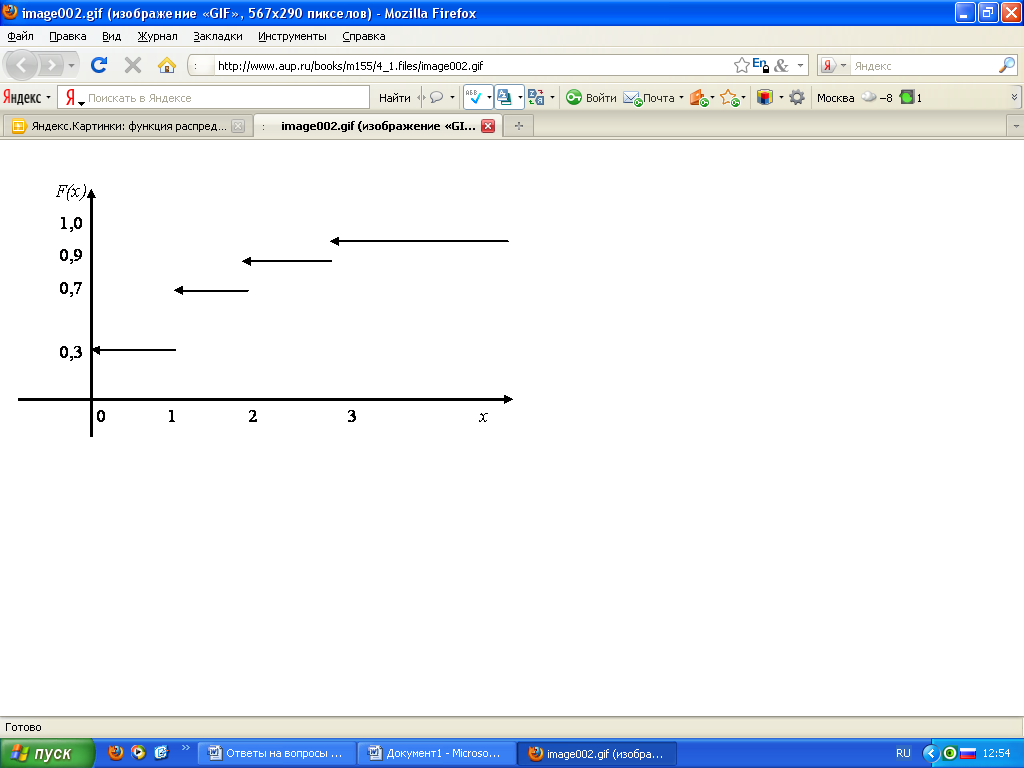
Свойства функции распределения:

1. F(x) – неубывающая функция своего аргумента: х₁<х₂, P(х₁)<P(х₂)

2. F(-∞)=1, F(+∞)=1

Ф ункция распределения любой дискретной СВ – кусочно-непрерывная ф-я. Скачки происходят в точках, соответствующих возможным значениям СВ, и равны вероятностям этих значений. По мере сокращения интервала изменяющейся СВ скачки становятся меньше и в итоге ф-я стремится к непр. функции, а сами величины становятся непр.