19. Предельные теоремы теории вероятностей. Неравенство Чебышева, неравенство Маркова. Закон Больших чисел (теорема Чебышева).

Практика изучения случайных явлений показывает, что хотя результаты отдельных наблюдений, даже проведенных в одинаковых условиях, могут сильно отличаться, в то же время средние результаты для достаточно большого числа наблюдений устойчивы и слабо зависят от результатов отдельных наблюдений.

Теоретическим обоснованием этого свойства случайных явлений является закон больших чисел.

Закон больших чисел:

В широком – при большом числе СВ их средний результат перестает быть случайным и м.б. предсказан с большой степенью определенности

В узком – ряд матем. теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.

В основе качественных и количественных утверждений закона больших чисел лежит неравенство Чебышева. Оно определяет верхнюю границу вероятности того, что отклонение значения случайной величины от ее математического ожидания больше некоторого заданного числа. Замечательно, что неравенство Чебышева дает оценку вероятности события для случайной величины, распределение которой неизвестно, известны лишь ее математическое ожидание и дисперсия.

Неравенство Чебышева – каково бы ни было «+»-е число α, Р_А, что величина Х отклонится от своего М(Х) не меньше, чем на α, ограничена сверху величиной D(X)/α².

Д ля любой СВ, имеющей М(Х) и D(X), справедливо неравенство:

Неравенство Чебышева для некоторых СВ:

1 ) Для СВ X=m при Х~Bi(n,p) c M(X)=np и D(X)=npq:

2 ) Для частости m/n события в n независимых испытаниях, в каждом из кот. оно может произойти с одной и той же p=M(m/n), и имеющей D(m/n)=pq/n:

В частности, есть обобщенное неравенство Чебышева: неравенство Маркова – если СВ Х принимает только неотрицательные значения и М(Х), то для любого «+»-го числа А верно неравенство:

Т.к. события x>A и х≤А противоположные, то заменяя выражение Р(x>A) выражением 1-Р(X≤A), придем к другой форме неравенства Маркова: Р(x≤A)≤1-[М(Х)^t/А^t].

Теорема Чебышева. Если Х₁,…, Х_n – попарно независимые СВ, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было «+»-е число ε, вероятность неравенства равенства

будет как угодно близка к 1, если число СВ будет достаточно велико. Другими словами:

.

Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых СВ, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического СВ от среднего арифметическогого их матожиданий будет по абс. величине сколь угодно малым.

Сущность теоремы заключается в том, что отдельные СВ могут иметь значительный разброс, а их среднее арифметическое рассеяно мало. Среднее арифметическое достаточно большого числа независимых СВ (дисперсии которых равномерно ограничены) утрачивает характер СВ.

Также эта теорема устанавливает связь между средним арифметически наблюдаемых значений СВ и ее M(X).

Р ассмотрим СВ Х с M(X) и D(X). Над этой величиной производится n независимых опытов и вычисляется сред. арифм. всех наблюдаемых значений СВ. Требуется найти числовые характеристики сред. арифм.

Само сред. арифметическое:

20. Следствия закона больших чисел (см. вопр. 19): теоремы Бернулли и Пуассона.

Закон больших чисел:

В шир. – при большом числе СВ их средний рез-т перестает быть случайным и м.б. предсказан с большой ст. определенности

В узком – ряд матем. теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних хар-к большого числа испытаний к некот. определенным постоянным.

Пусть мы производим n независимых опытов, в каждом может появиться некоторое событие А, вероятность которого в каждом опыте равна p.

Т 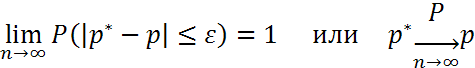еорема Бернулли: при неограниченном увеличении числа опытов n частость события А сходится по вероятности к его вероятности в отд. испытании, т.е.

Смысл т.Бернулли состоит в том, что при большом числе n повторных независимых испытаний практически достоверно, что частость события m/n – величина случайная, как угодной мало отличается от неслучайной величины p – вероятности события, т.к. практически перестает быть случайной.

Замечание. Т.Бернулли является следствием теоремы Чебышева, ибо частость события можно представить как сред. арифм. n независимых альтернативных СВ, имеющих один и тот же закон распределения.

(!) Т.Бернулли дает теоретическое обоснование замены неизвестной вероятности события его частостью, полученной в n повторных испытаниях, проводимых при одном и том же комплексе условий. Например, если P_A рождения мальчика неизвестна, то в качестве ее значения мы можем принять частость этого события.

Непосредственным обобщением т.Бернулли является т.Пуассона, когда вероятности события в каждом испытании различны.

Теорема Пуассона. Частость события в n повторных независимых испытаниях, в каждом из которых оно может произойти соответственно с вероятностями p₁,…,p_n, при неограниченном увеличении числа n сходится по вероятности к средней арифметической вероятностей события в отдельных испытаниях, т.е.:

Важная роль закона больших чисел в теоретическом обосновании методов матстатистики и ее приложений обусловила проведение ряда исследований, направленных на изучение общих условий применимости этого закона к последовательности СВ.

Например, тем-ра t воздуха в Москве X_i (i=1,…,365) каждый день года – величины случайные, подверженные существенным колебаниям в течение года, причем зависимые, т.к. на погоду каждого дня, очевидно, заметно влияет погода предыдущих дней. Однако среднегодовая тем-ра почти не меняется для Москвы в течение многих лет, являясь практически неслучайной, предопределенной.

Нахождение общих условий, выполнение которых обязательно влечет за собой статистич. устойчивость средних, представляет собой научную ценность исследований в области закона больших чисел.