5.3.2 Расчёт надёжности систем со сложной структурой

Во многих случаях рассмотренный выше способ расчёта надежности не может быть использован, так как не всегда структурная схема надёжности сводится к последовательно-параллельному соединению элементов.

Расчёт надёжности систем со сложной структурой рассмотрим на примере мостиковой структуры, изображенной на рис. 5.4 а, б. Данная структура не сводится к последовательно-параллельному соедине­нию элементов.

Мостиковая схема представляет собой параллельное соединение последовательных цепочек элементов с диагональными элементами, включенными между узлами различных параллельных ветвей (элемент 5 на рис. 5.4, а, и элементы 7 и 8 на рис. 5.4, б).

а)

б)

Рис. 5.4 Мостиковые схемы соединения элементов

Определим вероятность безотказной работы (вероятность отказа) мостиковой структуры, если известны вероятности безотказной работы (вероятности отказа) всех её элементов.

Метод перебора состояний. Каждый элемент системы может находиться в двух состояниях: состоянии работоспособности и состоянии отказа. При этом число состояний , где – число элементов системы.

Веро­ятность работоспособности системы при независимости отказов элементов определяется произведением вероятностей каждого из состояний

, (5.14)

вероятность отказа

, (5.15)

где – общее число работоспособных состояний, в каждом -м из которых число исправных элементов равно , а вышед­ших из строя – .

Метод перебора состояний эффективен только при малом количестве элементов n, поскольку число состояний системы составляет . Например, для схемы на рис. 5.4, а их количество составит 32, а для схемы на рис. 5.4, б – 256. Некоторого упрощения можно достигнуть, если в таблицу состояний включать только сочетания, отвечающие только работоспособному (или только неработоспособному) состоянию системы в целом.

Расчёт простейшей мостиковой структуры (рис. 5.4, а) методом перебора состояний представлен в табл. 5.1, где знаком плюс отмечены работоспособные состояния элементов, а знаком минус – неработоспо­собные. В данную таблицу включены только работоспособные сочетания элементов системы, что позволило снизить число состояний с 32 до 16.

Таблица 6.1

Расчёт мостиковой схемы методом перебора состояний

Номер состояния	Состояние элементов									Вероятность состояний
	1	2		3		4		5
1	+	+		+		+		+
2	-	+		+		+		+
3	+	-		+		+		+
4	+	+		-		+		+
5	+	+		+		-		+
6	+	+		+		+		-
7	-		+		-		+		+
8	-		+		+		-		+
9	-		+		+		+		-
10	+		-		-		+		+
11	+		-		+		-		+
12	+		-		+		+		-
13	+		+		-		+		-
14	+		+		+		-		-
15	-		+		-		+		-
16	+		-		+		-		-

Вероятность безотказной работы системы согласно (5.14)

.

Используя соотношение , выражение для определения вероятности безотказной работы системы примет вид

. (5.16)

В силу очень большого числа состояний системы, метод прямого перебора является весьма трудоемким и редко применяется на практике.

Метод разложения относительно особого элемента. Данный метод основан на формуле полной вероятности []. В анализируемой системе необходимо выделить особый элемент. Все его возможные состояния образуют полную группу . Если анализируемое состояние системы , то его вероятность

. (5.17)

Второй сомножитель в (5.17) определяет вероятность состоя­ния А при условии, что особый элемент находится в состоянии . Рассмотрение -го состояния особого элемента как безусловного (работоспособное и неработоспособное) позволяет упростить структурную схему надежности и свести ее к последовательно-параллельному соединению эле­ментов.

На мостиковой схеме (рис. 5.4, а) выделим эле­мент 5 в качестве особого с двумя возможными состояниями (1 – наличие и 2 – отсутствие цепи) ; . Это позволяет от структурной схемы, представленной на рис. 5.4, а, перейти при безусловно работоспособном состоянии элемента 5 к схеме, представленной на рис. 5.5, а. При отказе элемента 5 струк­турная схема имеет вид, представленный на рис. 5.5, 6. При этом выражение (5.17) можно представить в виде

, (5.18)

где и – вероятности безотказной работы и отказа 5-го (особого) элемента, и – вероятности работоспособного состояния системы при условии, что особый элемент 5 абсолютно надежен и отказал.

а)

б)

Рис. 5.5 Структурные схемы мостикового соединения эле­ментов, соответствующих наличию цепи (а) в элементе 5 и ее отсутствию (б)

В соответствии с (5.1) и (5.7) имеем

;

;

(5.19)

Легко убедиться, что в случае подстановки соотношения формула (5.19) обращается в (5.16).

Данный метод справедлив и при разложении относительно нескольких «особых» элементов. Например, для мостиковой схемы с двумя диагональными элементами 7 и 8 (рис. 5.4, б) выражение (5.19) будет иметь вид

. (5.20)

Метод минимальных путей и сечений.

Минимальный путь – это последовательный набор работоспособных элементов системы, который обеспечивает её работоспособность, а отказ любого из них приводит к её отказу.

При формировании пути, принимая, что все элементы системы находятся в не­работоспособном состоянии, последовательным переводом эле­ментов в работоспособное состояние производят подбор вари­антов цепочек элементов, которые в случаи своей работоспособности обеспечивали работоспособность системы. Набор элементов образует минимальный путь, если исключе­ние любого элемента из набора приводит к отказу пути. Из этого вытекает, что в пределах одного пути элементы находят­ся в последовательном соединении, а сами пути включаются парал­лельно.

Для мостиковой схемы (рис. 5.4, а) набор минимальных путей представлен на рис. 5.6, а.

1

3

1

1

2

3

2

4

5

5

2

4

3

4

5

1

4

5

2

3

а)

б)

Рис. 5.6 Набор минималь­ных путей (а) и сечений (б)

Вероятность безотказной работы данной схемы представляет собой оценку надёжность сверху и может быть вычислена согласно (5.1) и (5.7)

.

Минимальное сечение – это последовательный набор неработоспособных элементов системы, отказ которых приводит к отказу системы, а восстановление работоспособности любого из них – к восстановлению работоспособности системы.

При определении минимальных сечений осуществляется подбор минимального числа элементов, перевод которых из ра­ботоспособного состояния в неработоспособное вызывает отказ системы. При правильном подборе элементов сечения возвра­щение любого из элементов в работоспособное состояние вос­станавливает работоспособное состояние системы. Поскольку отказ каждого из сечений вызывает отказ системы, то они соединяются последовательно. В пределах каждого сечения элементы соединяются параллельно, так как для работы систе­мы достаточно наличия работоспособного состояния любого из элементов сечения.

Для мостиковой схемы (рис. 5.4, а) набор минимальных сечений представлен на рис. 5.6, б. Вероятность безотказной работы такой схемы представляет собой оценку надёжность снизу и может быть вычислена согласно (5.1) и (5.7)

.

На основе оценки надёжности сверху и снизу получается двусторонняя оценка, выражающаяся через неравенство

,

где – истинная вероятность безотказной работы системы.

Для систем состоящих из не большого числа элементов вероятность безотказной работы сверху и снизу может совпадать. Для более сложных систем этого может не произойти, поэтому для оценки надежности методы минимальных путей и минимальных сечений следует применять совместно.

Логико-вероятностный метод анализа надежности. Теоретической основой данного метода является математическая логика (булева алгебра) [], которая оперирует с логическими выражениями, имеющими значения «истинно» (1) или «ложно» (0). Логические выражения называемые функциями алгебры логики (ФАЛ) являются функциями логических переменных , , …, , каждая из которых также имеет значения 0 или 1.

ФАЛ образуются при помощи трех основных операций: логического отрицания или инверсии ( ), сложения (дизъюнкции, ИЛИ), обозначаемого зна­ком «+» или « », и умножения (конъюнкции, И), обозначаемого « » или « ».

ФАЛ имеют следующие формы:

Элементарная конъюнкция – это логическое произведение переменных и их отрицаний (инверсий), причем каждая переменная должна входить в выражение только один раз ( или ).

Элементарная дизъюнкция – это логическая сумма переменных и их инверсий, причем каждая переменная должна входить в выражение только один раз ( или ).

Дизъюнктивная нормальная форма (ДНФ) – это дизъюнкция элементарных конъюнкций ( ).

Конъюнктивная нормальная форма (КНФ) – это конъюнкция элементарных дизъюнкций ( ).

Совершенная дизъюнктивная нормальная форма (СДНФ) – это ДНФ, в каждом члене которой представлены все переменные (или их инверсии) функции. Для перехода от ДНФ к СДНФ необходимо в каждый из членов, в которых представлены не все аргументы, ввести выражение вида , где – отсутствующий в члене аргумент.

Совершенная конъюнктивная нормальная форма (СКНФ) – это КНФ, в каждом члене которой представлены все переменные (или их инверсии) функции. Переход от КНФ к СКНФ аналогичен рассмотренному выше переходу от ДНФ к СДНФ.

Для преобразования логических выражений используются следующие законы математической логики:

• закон тавтологии: ; ;

• законы нулевого элемента: ; ;

• законы единичного элемента: ; ;

• закон дополнительного элемента (в булевой алгебре дополнительным элементом является инверсия): ; ;

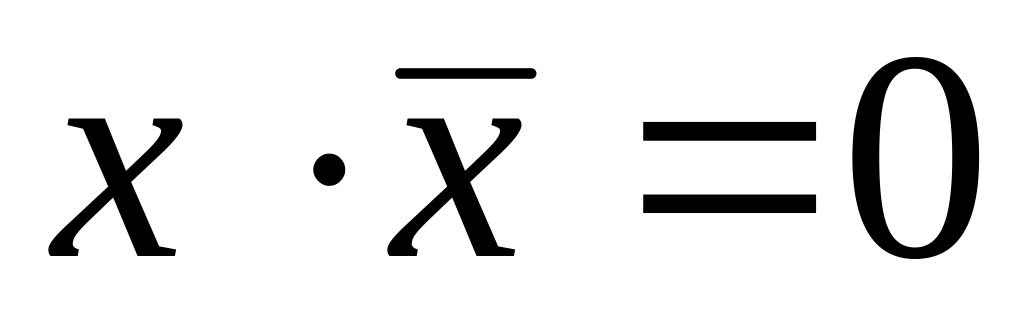• закон коммутативности: ; ;

• закон ассоциативности: ; ;

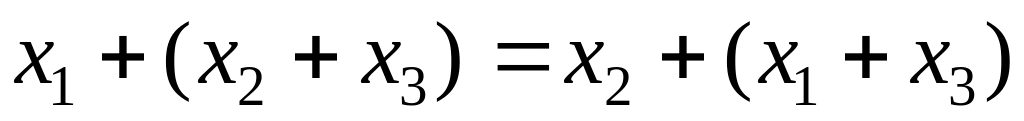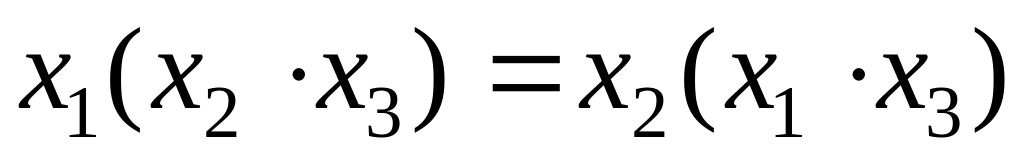• закон дистрибутивности: ; ;

• закон дуальности (инверсии, Де-Моргана): ; ;

• закон поглощения: ; .

Применительно к расчетам надёжности систем, ФАЛ называются функциями работоспособности (надежности), где состояния элементов – работоспособное, соответствующее логической 1 и – неработоспособное, соответствующее логическому 0. Функции работоспособности могут зада­ваться в виде словесного описания функционирования системы, таблицами истинности, логическими выражениями или графиками.

Рассмотрим структурную схему представляющую собой последовательное (основное) соединение элементов (рис. 5.7).

Рис. 5.7 Структурная схема последовательного (основного) соединения элементов

Обозначим , i=1, 2, … , n – состояние i-го элемента системы, обозначаемое 0, если элемент находится в неработоспособном состоянии, и 1, если в работоспособном. В данном случае система работоспособна, если работоспособны все её элементы. Тогда ФАЛ является конъюнкцией логических переменных, т.е. , представляющей собой СДНФ системы.

Подставляя вместо логических переменных вероятности работоспособных состояний элементов и проводя замену конъюнкции на алгебраическое умножение, получим

.

Рассмотрим структурную схему представляющую собой параллельное (резервное) соединение двух неравнонадежных элементов (рис. 5.8).

Рис. 5.8 Структурная схема параллельного (резервного) соединения двух неравнонадежных элементов

На рис. 5.8 и – состояния элементов системы. Для получения ФАЛ составим таблицу истинности (табл. 5.2), где 1 – работоспособное состояние элемента, 0 – неработоспособное состояние элемента.

В данном случае система работоспособна, если работоспособны оба элемента (1,1) или один из них ((0,1) или (1,0)). Тогда работоспособное состояние системы описывается следующей ФАЛ

.

Таблица 5.2

Таблица истинности для параллельного (резервного) соединения

двух неравнонадежных элементов

0	0	0
0	1	1
1	0	1
1	1	1

Данная функция алгебры логики является СДНФ. Заменяя операции дизъюнкции и конъюнкции на алгебраические операции умножения и сложения, а логические переменные – на соответствующие вероятности состояния элементов, получим выражение вероятности безотказной работы системы

.

Р ассмотрим мостиковую схему с одним диагональным элементом c позиции алгебры логики (рис. 5.8).

Рис. 5.8 Структурная схема мостиковой системы с неравнонадежными элементами

Для анализа надёжности данной структуры воспользуемся, рассмотренным выше, методом минимальных путей и сечений. Обозначим , , , , – состояния 1, 2 , 3, 4 и 5 элементов системы соответственно, равные 1, если элемент работоспособен, и 0, если неработоспособен.

В данном случае кратчайшими путями, образующими работоспособную систему, будут: , , , . Тогда функция работоспособности системы

. (5.21)

Минимальными сечениями, образующими работоспособную систему, будут , , , . Тогда функция работоспособности системы

. (5.22)

Однако, полученные ФАЛ (5.21) и (5.22) не являются выражениями для определения вероятности безотказной работы системы. Данные ФАЛ позволяют, не составляя таблицы истинности, получить СДНФ или СКНФ, которые дадут возможность получить вероятность безотказной работы системы путем подстановки в ФАЛ вместо логических переменных соответствующих значений вероятностей безотказной работы, заменив операции конъюнкции и дизъюнкции на алгебраические операции умножения и сложения.

Для получения СДНФ необходимо каждый дизъюнктивный член ФАЛ умножить на ( ), где – недостающий аргумент, и затем раскрыть скобки. СДНФ системы применительно к методу кротчайших путей будет иметь вид

. (5.23)

После преобразования по правилам алгебры логики выражение (5.23) примет вид

.

Подставляя в СДНФ вместо , , , , вероятности безотказной работы , , , , и используя соотношения , получим выражение для определения вероятности безотказной работы системы

.

Расчет вероятности безотказной работы системы по методу минимальных сечений производится аналогично. Для простейшей мостиковой схемы (рис.6.8) конечные выражения для определения вероятности безотказной работы системы по обеим методам будут совпадать.