В.3. Основные правила дифференцирования

1. с’ = 0;

2. x’ = 1;

3. (u + v)’ = u’ + v’;

4. (c∙u)’ = c∙u’;

5. (u∙v)’ = u’∙v + u∙v’;

6. (u∙v∙w)’ = u’∙v∙w + u∙v’∙w + u∙v∙w’;

7. .

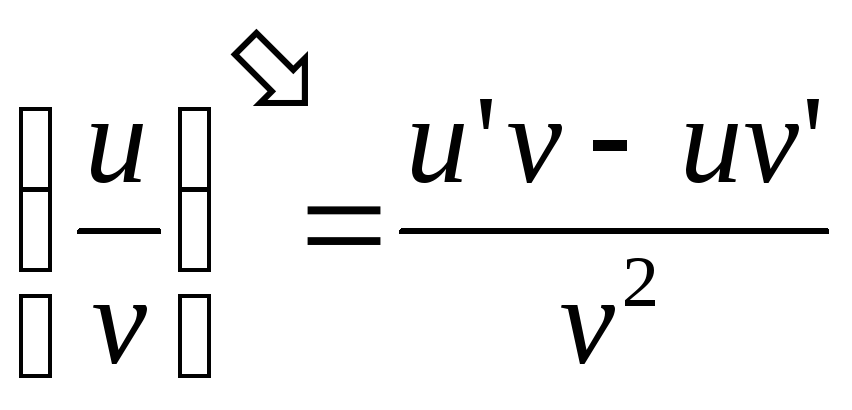В.4. Производная сложной и обратной функций

Если у есть функция от и: у = f(u), где и в свою очередь есть функция от аргумента х: u = φ(x), т.е. если у зависит от х через промежуточный аргумент и, то у называется сложной функцией от х (функцией от функции): y = f(φ(x)).

Теорема. Производная сложной функции , где , где y и u – дифференцируемые функции своих аргументов, равна произведению ее производной по промежуточному аргументу на производную этого аргумента по независимой переменной:

или y’_x = y’_u u’_x

.

Пусть –дифференцируемая и строго монотонная функция на промежутке X, – обратная к ней и непрерывная на соответствующем промежутке Y.

Теорема. Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции, т.е.

В. 5. Производные основных элементарных функций

С учётом полученного правила дифференцирования сложной функции таблицу производных можно записать в следующем виде:

Таблица производных

№	Функция у	Производная у’
1	С	0
2	x	1
3	un	n∙un-1∙ u’
4
5
6	eu	eu∙u’
7	au	au∙ln a∙u’
8	ln u
9	loga u
10	sin u	cos u∙u’
11	cos u	– sin u∙u’
12	tg u
13	ctg u
14	arcsin u
15	arcos u	–
16	arctg u
17	arcctg u	–

Пример 1. Найти производную функции:

а) у = х + 2; б) y = (2x – 3)(3x + 2); в) у = ; г) у =; д) у =(x³ – 2x² + 5)⁶; е) ; ж) ; з) y = tg(3x² – 1); и) .

Решение. а) у = х + 2

Используя правило дифференцирования (3) и формулы (1), (2), имеем:

у' = (x + 2)’ = (x)’ + (2)’ = 1 + 0 = 1.

б). y = (2x – 3)(3x + 2)

y’ = ((2x – 3)(3x + 2))’ = (2x – 3)’∙(3x + 2) + (2x – 3)∙(3x + 2)’ = 2∙(3x + 2) + (2x – 3)∙3 = 12x – 5. Здесь мы использовали правило дифференцирования (5).

в) у =

Используя правило дифференцирования (7), имеем

у’ ==.

г) у =

Найдем производную, используя правило дифференцирования (4) и формулу (3).

у' =.

д) у =(x³ – 2x² + 5)⁶

Пусть x³ – 2x² + 5 = и, тогда у = и⁶. По формуле (3), получим у’ = (и⁶)’ = 6u⁵∙u’= 6(x³ – 2x² + 5)⁵∙(x³ – 2x² + 5)’ = 6(x³ – 2x² + 5)⁵∙(3x² – 4x).

е)

По правилу дифференцирования (7) и формуле (10) получим:

=.

ж)

Используя формулы (4) и (10), имеем:

.

з) y = tg(3x² – 1).

По формуле (12) имеем:

y' = (tg(3x² – 1))’ =.

и) .

По формуле (8), а также (3), (4), (5) имеем:

=

=.
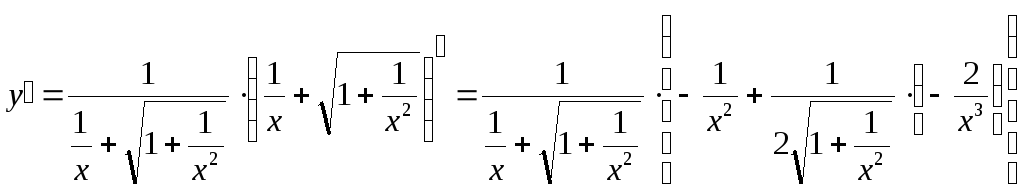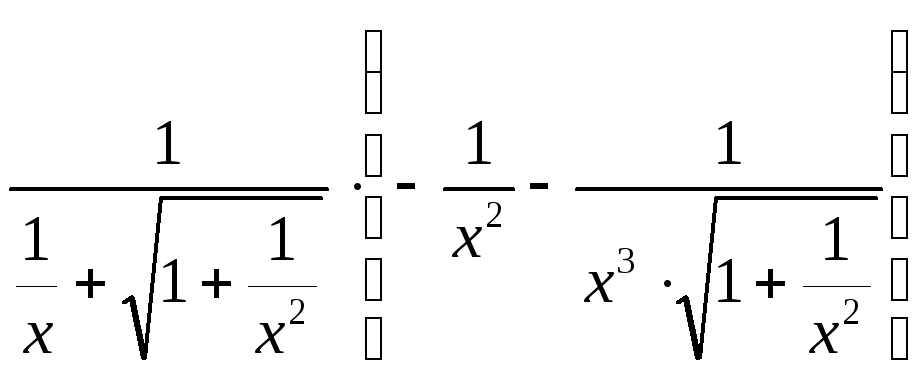