мат. стат

Основные понятия математической статистики.

Математическая статистика – раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений для выявления существующих закономерностей. Предметом математической статистики является изучение случайных величин (или случайных событий, процессов) по результатам наблюдений. Совокупность всех подлежащих изучению объектов или возможных результатов всех мыслимых наблюдений, производимых в неизменных условиях над одним объектом, называется генеральной совокупностью. Зачастую проводить сплошное обследование, когда изучаются все объекты, трудно или дорого, а иногда и невозможно. В этих случаях наилучшим способом обследования является выборочное наблюдение: выбирают из генеральной совокупности часть ее объектов («выборку») и подвергают ее изучению. Выборочной совокупностью (выборкой) называют совокупность объектов, отобранных случайным образом из генеральной совокупности. Более строго: выборка – это последовательность X1, X2, … Xn независимых одинаково распределенных случайных величин, распределение каждой из которых совпадает с распределением генеральной случайной величины. Число объектов (наблюдений) в совокупности, генеральной или выборочной, называется ее объемом; обозначается соответственно через N и n. Конкретные значения выборки, полученные в результате наблюдений (испытаний), называют реализацией выборки и обозначают строчными буквами x1, х2 …хn. Метод статистического исследования, состоящий в том, что на основе изучения выборочной совокупности делается заключение о всей генеральной совокупности, называется выборочным. Различают выборки с возвращением (повторные) и без возвращения (бесповторные). В первом случае отобранный объект возвращается в генеральную совокупность перед извлечением следующего; во втором – не возвращается. На практике чаще используется бесповторная выборка.

Статистическое распределение выборки. Эмпирическая функция распределения.

Пусть изучается некоторая случайная величина Х. С этой целью над случайной величиной Х производится ряд независимых опытов (наблюдений). В каждом из этих опытов величина Х принимает то или иное значение. Пусть она приняла n1 раз значение х1, n2 раз – значение х2, …,nk раз – значение хк. При этом n1 n2 ... nk n – объем выборки. Значения x1, х2 …хк называются вариантами

Графическое изображение статистического распределения.

Статистическое распределение изображается графически (для наглядности) в виде так называемых полигона и гистограммы. Полигон, как правило, служит для изображения дискретного (т.е. варианты отличаются на постоянную величину) статистического ряда. Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами (х1,n1), (x2,n2), …, (xk,nk); полигоном частостей – с координатами (х1,p1), (x2,p2), …, (xk,pk). Варианты xi откладываются на оси абсцисс, а частоты и, соответственно, частости – на оси ординат. Полигон частостей является статистическим аналогом многоугольника распределения. Для непрерывно распределенного признака (т.е. варианты могут отличаться один от другого на сколь угодно малую величину) можно построить полигон частот, взяв середины интервалов в качестве значений x1, x2,….,xk. Более употребительна так называемая гистограмма. Гистограммой частот (частостей) называют ступенчатую фигуру, состоящую из прямоугольников, основаниями

которых служат частичные интервалы длины h, а высоты равны отношению ni – h

плотность частоты ( pi – плотности частости). Очевидно, площадь гистограммы h

частот равна объему выборки, а площадь гистограммы частостей равна единице.

Числовые характеристики статистического распределения

Для выборки можно определить ряд числовых характеристик, аналогичных тем, что в теории вероятностей определялись для случайных величин. Пусть статистическое распределение выборки объема n имеет вид:

Генеральной средней xг называют среднее арифметическое значений

интервального статистического ряда в равенстве хi ,берут середины его интервалов, а ni – соответствующие им частоты. Групповой средней называют среднее арифметическое значений признака, принадлежащих группе. Общей средней х называют среднее арифметическое значений признака, принадлежащих всей совокупности. Зная групповые средние и объемы групп,

можно найти общую среднюю: общая средняя равна средней арифметической групповых средних, взвешенной по объемам групп. Генеральной дисперсией Dг называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения xг . Выборочной дисперсией Dв называется среднее арифметическое квадратов отклонений

дисперсией называют дисперсию значений признака, принадлежащих группе,

xi , j – номер группы, xj – групповая средняя группы j, N j ni объем группы j.

Внутригрупповой дисперсией называют среднюю арифметическую дисперсий,

состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой

. Особенность выборочного среднего квадратического отклонения состоит в том, что оно измеряется в тех же единицах, что и изучаемый признак. При решении

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии: г DГ . Величина S 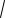S2

называется исправленным выборочным средним квадратическим отклонением.

Для непрерывно распределенного признака формулы для выборочных средних будут такими же, но за значения х1, х2, х3,…, хк надо брать не концы

Оценки параметров распределения.

Статистической оценкой параметра теоретического распределения называют его приближенное значение, зависящее от данных выбора. Функцию результатов наблюдений (т.е. функцию выборки) называют статистикой. Статистика используемая в качестве приближенного значения неизвестного параметра генеральной совокупности, называется ее точечной оценкой.

Точечной оценкой неизвестного параметра называют число (точку на числовой оси), которое приблизительно равно оцениваемому параметру и может

заменить его с достаточной степенью точности в статистических расчетах.

Для того чтобы точечные статистические оценки обеспечивали “хорошие” приближения неизвестных параметров, они должны быть несмещенными,

состоятельными и эффективными.

Пусть – точечная оценка неизвестного параметра .

Несмещенной называют такую точечную статистическую оценку ,

математическое ожидание которой равно оцениваемому параметру:

M .

Состоятельной называют такую точечную статистическую оценку, которая при n стремится по вероятности к оцениваемому параметру. В частности, если дисперсия несмещенной оценки при n стремится к нулю, то такая оценка оказывается и состоятельной.

Эффективной называют такую точечную статистическую оценку, которая при фиксированном n имеет наименьшую дисперсию.

Оценка математического ожидания

Пусть имеется случайная величина Х с математическим ожиданием m и дисперсией D, при этом оба эти параметра неизвестны. Над величиной Х произведено N независимых экспериментов, в результате которых была получена совокупность N численных результатов x1, x2, …, xN. В качестве оценки математического ожидания естественно предложить среднее арифметическое

1 N

наблюдаемых значений т* N i 1 xi .

Оценка математического ожидания является несмещенной.

Оценка дисперсии

При больших объемах выборки для оценки дисперсии используют формулу:

N

параметров распределения: метод моментов, метод максимального правдоподобия и метод наименьших квадратов. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками. Оценка неизвестного параметра называется интервальной, если она определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надежность

интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал 1 , 2 , относительно которого с заранее выбранной вероятностью можно сказать, что внутри этого интервала находится точное значение оцениваемого параметра. Интервал 1 , 2 накрывающий с вероятностью истинное значение параметра , называется доверительным интервалом, а вероятность – надежностью оценки или доверительной вероятностью. Величина выбирается заранее, ее выбор зависит от конкретно

решаемой задачи. Надежность принято выбирать равной 0,9; 0,95; 0,99 или

0,999.

Доверительный интервал для математического ожидания при известной дисперсии:

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение этого распределения

известно. С надежностью можно утверждать, что доверительный интервал

(приложение 4) находят аргумент t , которому соответствует значение функции Лапласа.

Доверительный интервал для математического ожидания при неизвестной дисперсии:

Пусть количественный признак X генеральной совокупности распределено нормально, причем среднее квадратическое отклонение неизвестно. Доверительный интервал, покрывающий неизвестный параметр a с

заданным n и можно найти t .

Доверительный интервал для среднего квадратического отклонения нормального распределения:

Пусть количественный признак X генеральной совокупности распределен нормально. Доверительный интервал, покрывающий с заданной надежностью

Оценка истинного значения измеряемой величины

Пусть производится n независимых равноточных измерений некоторой физической величины, истинное значение а которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины X1, X2, … Xn . Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии 2 (измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов. доверительных интервалов. Поскольку обычно неизвестно, следует пользоваться формулами, доверительного интервала для оценки математического ожидания нормального распределения при неизвестном .

Оценка точности измерений

В теории ошибок принято точность измерений (точность прибора) характеризовать с помощью среднего квадратического отклонения случайных ошибок измерений. Для оценки используют «исправленное» среднее

квадратическое отклонение s. Поскольку обычно результаты измерений взаимно независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае равноточных измерений), то доверительные интервалы для оценки среднего квадратического отклонения нормального распределения, применим для оценки точности измерений.

Числовые характеристики вариационного ряда.

Кроме выборочной средней и выборочной дисперсии в качестве описательных характеристик вариационного ряда (или полученного из него статистического распределения выборки) используется медиана, мода, размах вариации (выборки) и т.д.

Размахом варьирования называется число R xmax xmin , где xmax –

наибольший, – наименьший вариант ряда. Размах является простейшей характеристикой рассеяния вариационного ряда.

Модой M0 вариационного ряда называется вариант, имеющий наибольшую частоту.

Медианой Me вариационного ряда называется значение признака,

приходящееся на середину ряда.

Коэффициентом вариации V называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной

средней: V В 100%. Коэффициент вариации служит для сравнения величин xВ

рассеяния по отношению к выборочной средней двух вариационных рядов: тот из рядов имеет большее рассеяние по отношению к выборочной средней, у которого коэффициент вариации больше.

Гипотезы. Основные понятия

Одна из часто встречающихся на практике задач, связанных с применением статистических методов, состоит в решении вопроса о том, должно ли на основании данной выборки быть принято или, напротив, отвергнуто некоторое предположение (гипотеза) относительно генеральной совокупности (случайной величины). Статистической называют гипотезу о виде неизвестного распределения или о параметрах неизвестных распределений. Нулевой называют выдвинутую гипотезу H0 . Конкурирующей называют

гипотезу H1 , которая противоречит нулевой. Простой называют гипотезу,

содержащую только одно предположение. Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Вероятность совершить ошибку первого рода принято обозначать через ; ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Вероятность ошибки 2-го рода обозначается через . Величину 1 , т.е. вероятность недопущения ошибки второго рода,

называется мощностью критерия. Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно. Обозначим эту величину в целях общности через K. Статистическим критерием (или просто критерием) называют случайную величину K, которая служит для проверки нулевой гипотезы. Наблюдаемым значением Кнабл называют значение критерия, вычисленное по выборкам. Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают. Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы

– гипотезу принимают. Критическими точками (границами) ккр называют точки, отделяющие критическую область от области принятия гипотезы. Правосторонней называют критическую область, определяемую неравенством K kкр , где kкр – положительное число. Левосторонней называют критическую область, определяемую неравенством K kкр , где kкр – отрицательное число.

Односторонней называют правостороннюю или левостороннюю критическую область. Двусторонней называют критическую область, определяемую неравенствами K k1 , K k2 , где k2 k1.

Сравнение дисперсий и математических ожиданий

Правило 1. Для того чтобы при заданном уровне значимости проверить нулевую гипотезу H0 : D(X) D(Y) о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе H1 : D(X) D(Y), надо вычислить наблюдаемое значение критерия (отношение большей исправленной

дисперсии к меньшей) Fнабл sб2 и по таблице критических точек распределения sм2

Фишера-Снедекора, по заданному уровню значимости и числам степеней

нормальных генеральных совокупностей с известными дисперсиями при конкурирующей гипотезе H1 : M(X) M(Y), надо вычислить наблюденное