В.8. Вычисление пределов

При вычислении пределов используют то, что предел постоянной равен самой постоянной, а также основные теоремы о пределах. Рассмотрим вычисление пределов на примерах.

Пример 7. Найти .

Решение. Так как под знаком предела стоит непрерывная в точке х=1 функция, то, используя определение непрерывной функции, имеем: .

Ответ. .

Пример 8. Найти .

Решение. Функция при х=1 не определена («неопределенность типа »), и, следовательно, не является непрерывной в этой точке. Но при всех других значениях х

.

Полученная функция определена и непрерывна в точке х=1, поэтому

==. Ответ: .

Пример 9. Найти

Решение. Здесь требуется найти предел отношения двух бесконечно больших величин. О таком пределе заранее ничего определенного сказать нельзя («неопределенность типа »). Преобразуем функцию под знаком предела, вынося за скобки х в старшей степени, и используем свойства бесконечно малых и бесконечно больших величин. Тогда имеем:

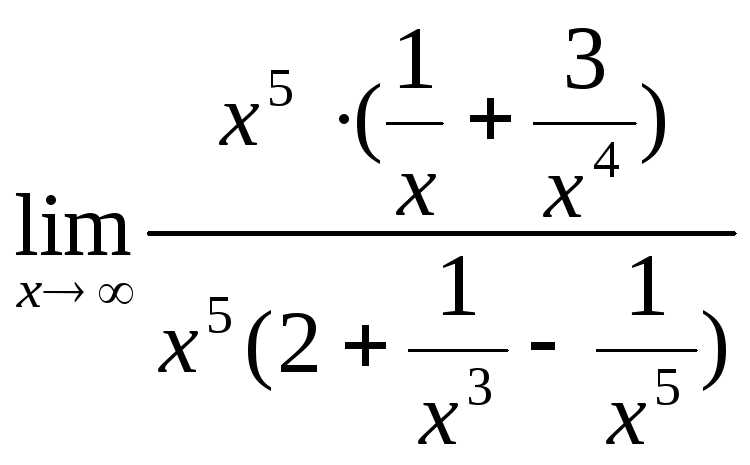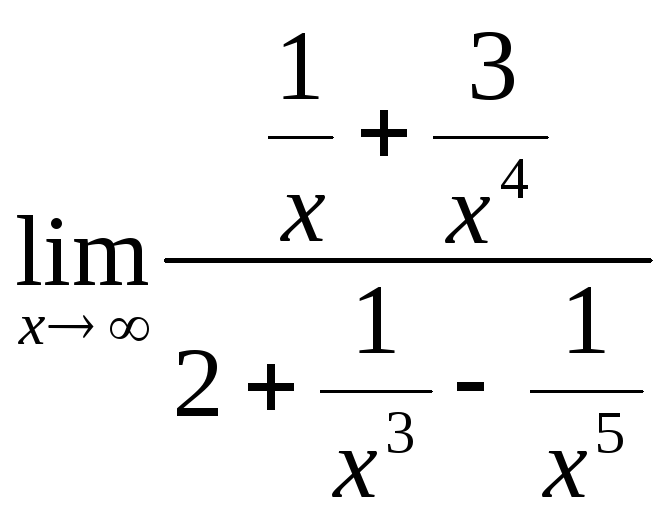==== 0.

Ответ: 0.

Пример 10. Найти .

Решение. Такого типа примеры решаются переводом иррациональности из числителя в знаменатель и, наоборот, из знаменателя в числитель. Здесь мы имеем предел разности двух положительных бесконечно больших величин («неопределенность типа [–]»). От этой неопределенности избавимся, дополнив функцию до разности квадратов:

= = = .

Следовательно, =

Ответ: 0.

Пример 11. Найти .

Решение. Выделим у дроби целую часть:

.

Чтобы использовать второй замечательный предел (или ), обозначим . Тогда при х→∞ у→0, причем . Т.о. =.

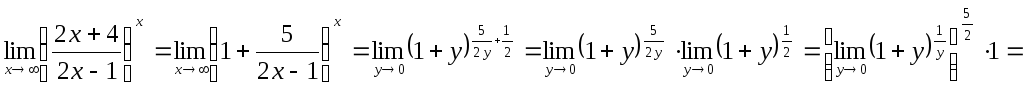Ответ: .

Тема 3. Дифференциальное исчисление функций одной переменной в.1. Задачи, приводящие к производной. Задача о касательной:

Пусть на плоскости ОХY дана непрерывная кривая у=f(х) и необходимо найти уравнение касательной к этой кривой в т. М(х, у).

Дадим аргументу х приращение и перейдем по кривой у=f(х) от т. М(х,у) к т. М(х+,f(х+). Проведем секущую М.

Под касательной к кривой у=f(х) в т. М понимают предел положительной секущей М при приближении т. М к М, т. е. при .

Уравнение прямой, проходящей через точку М, имеет вид: у – f(х)=k(х– х₀ ). k-угловой коэффициент может быть найден из : k= tg =. Отсюда – угловой коэффициент касательной.

Задача о скорости движения:

Пусть вдоль некоторой прямой движется точка по закону , где s – пройденный путь, t – время. Надо найти скорость точки в момент t₀.

К моменту пройденный путь составит, а к моменту : . Тогда за время средняя скорость . Чем меньше , тем лучше средняя скорость характеризует движение точки в момент t₀. Поэтому под скоростью в момент t₀ естественно понимать предел средней скорости за промежуток от t₀ до, когда : .

В.2. Определение производной функции

Пусть функция y = ƒ(x) определена на множестве Х. Возьмём т.хХ. Дадим значению х приращение . Тогда y подучит приращение .

Определение. Производной функции y = ƒ(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

.

Другие обозначения:

Дифференцирование функции – это нахождение производной этой функции. Если функция имеет в точке x производную (конечную), то она называется дифференцируемой в этой точке. То же можно сказать о дифференцировании функции на промежутке X.

Геометрический смысл производной: производная – угловой коэффициент или тангенс угла наклона касательной, проведенной к кривой y= f(x) в точке x₀ , с осью Ох.

Уравнение касательной к кривой y= f(x) в точке x₀: .

Механический смысл: производная пути по времени - есть скорость точки в момент t₀ , т.е. .

Теорема (зависимость между непрерывностью и дифференцируемостью): Если функция y= f(x) дифференцируема в точке x₀, то она в этой точке непрерывна.

Обратная теорема, вообще говоря, не верна, т.е. непрерывная функция может быть не дифференцируемой в точке x₀ , например, функция y =|x| в точке x=0.

Поэтому непрерывность функции является необходимым, но не достаточным условием дифференцируемости функции. В математике известны непрерывные функции, не дифференцируемые ни в одной точке.

Замечание. Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на промежутке X , то функция называется гладкой на этом промежутке. Если производная допускает конечное число точек разрыва 1-го рода, то она называется кусочно-гладкой на данном промежутке.