В.5. Элементарные функции

Функция называется явной, если она задана формулой вида y = f(x) (правая часть не содержит зависимой переменной).

Функция называется неявной, если она задана уравнением F(x, y) = 0, не разрешенным относительно зависимой переменной.

Пусть функция y = f(x) – функция от независимой переменной х с областью определения Х и областью значений Y. Поставим в соответствие единственное значение , при котором f(x) = y. Тогда полученная функция х = φ(у), определенная на промежутке Y с областью значений Х, называется обратной (обратную функцию также обозначают y = f ^-1(x)).

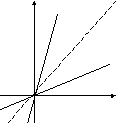
Для любой строго монотонной функции существует обратная функция. Графики взаимно обратных функций симметричны относительно прямой у = х (биссектрисы 1-го и 3-го координатных углов).

Пример 2. Для функции у = 3х найти обратную.

Функция у = 3х монотонная (возрастающая), следовательно, она имеет обратную. Для того чтобы получить формулу обратной функции выразим переменную х через у:

. А затем полученную формулу запишем в привычном виде (поменяем х и у местами): - это и есть обратная функция к данной.

у у = х у = 3х О х

Пусть функция y = f(и) – функция переменной и определена на множестве U с областью значений Y, а переменная и – функция переменной х: и = φ(х), определена на множестве Х с областью значений U. Тогда заданная на множестве Х с областью значений Y функция y = f[φ(х)] называется сложной функцией (композицией функций, функцией от функции).

Например, у = cos(x²+x) – сложная функция, т.к. ее можно представить в виде , у = cosи, где и = x²+x.

Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.

Например, функция – элементарная (пример неэлементарной функции у = |x|).

Классификация функций. Элементарные функции делятся на:

1) Алгебраические (полученные с помощью конечного числа алгебраических действий над аргументом). К ним относятся:

• целая рациональная функция (многочлен): ;

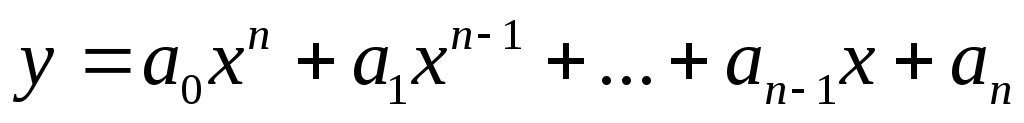• дробно-рациональная функция – отношение двух многочленов;

• иррациональная функция (в составе операций над аргументом есть извлечение корня).

2) Неалгебраические (или трансцендентные). К ним относятся: показательная, логарифмическая, тригонометрические, обратные тригонометрические.

В.6. Интерполирование функций

Интерполирование – приближенное вычисление неизвестных значений функции по известным ее значениям в заданных точках.

Наиболее простым является линейное интерполирование, при котором допускается, что приращение функции пропорционально приращению аргумента.

Пример 3. Значение функции известно в точках a и b. С помощью линейной интерполяции найти значение функции в точке с.

а	f(a)	b	f(b)	c
2	2,42	2,04	2,88	2,008

Решение. Значение с лежит между а и b. Формула линейного интерполирования:

f(c)  f(a) + , где h = b – a, f = f(b) – f(a).

Подставляя в формулу известные значения из таблицы, получим:

f(2,008)  2,42 + = 2,512. Ответ. f(2,008)  2,512.