4.3. Метод интегрирования по частям

Пусть u = u(x), v = v(x) – дифференцируемые функции.

По свойству дифференциала или .

Интегрируя обе части равенства, получим:

- формула интегрирования по частям.

Метод заключается в следующем: подынтегральное выражение разбивается на 2 множителя u и dv. Далее, при переходе к правой части формулы, первый множитель дифференцируется, а второй – интегрируется: , .

Этот метод применяется для двух групп интегралов:

I. ; ; (где m=const). В этой группе в качестве u выбирают х, а остальная часть подынтегрального выражения принимается за dv (u = x).

II. ; ; ; ; (где m=const). В этой группе xdx = dv.

Пример 4. .

В нашем случае интеграл относится к I-ой группе интегралов, поэтому в качестве u возьмем 5х – 2 : u = 5х – 2, dv = e^3x∙dx.

= =

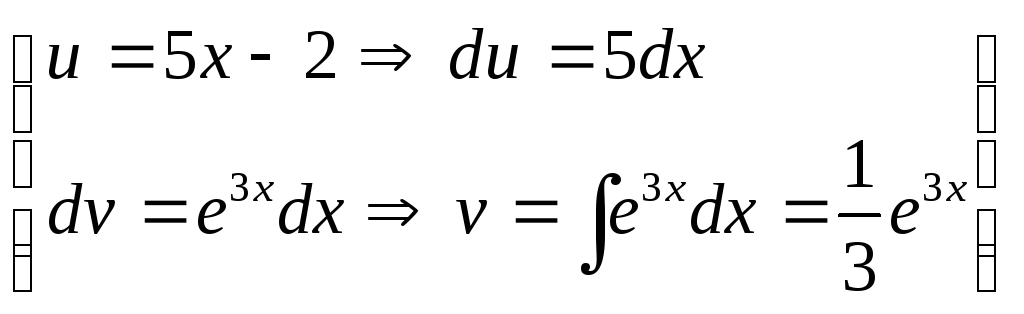(по формуле интегрирования по частям) = =

= .

Ответ: = .

В.5. Интегрирование отдельных классов функций

5.1. Интегрирование простейших рациональных дробей

Рациональной дробью называется отношение двух многочленов

R(x)=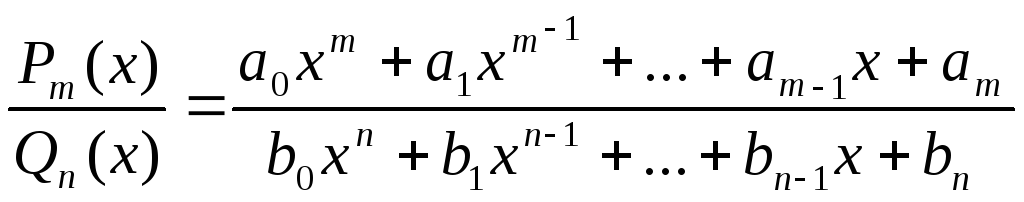

где a и - и это действительные числа ( i= 0, j=0, )

если m < , то дробь называется правильной,

m , то дробь называется неправильной

Любую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной рациональной дроби.

Простейшие рациональные дроби и их интегрирование:

1 тип: , (A, a, bR)

2 тип: , (A, a, b, kR), k

3 тип:

Первый вычисляется методом замены переменной: +С, а второй интеграл – табличный.

4 тип: 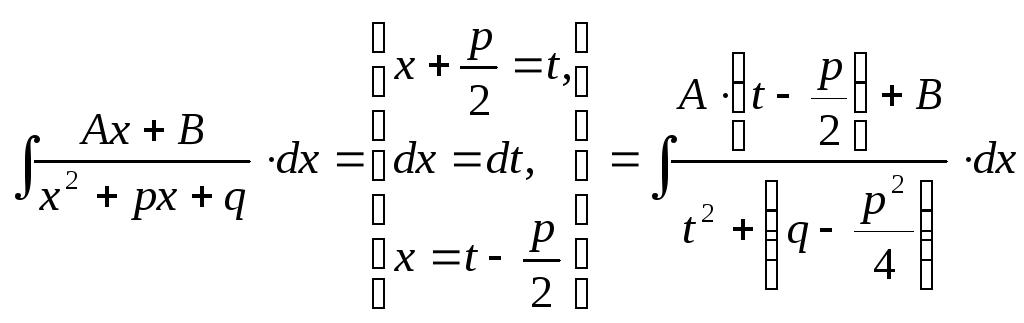, где ( не имеет действительных корней).

Пример 1. =…

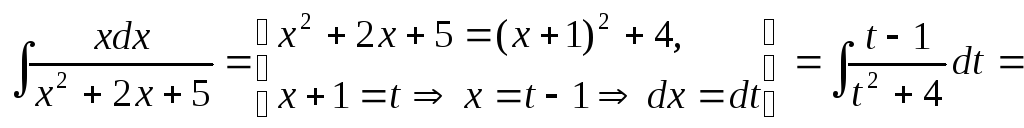
5 тип: Общий случай: если подынтегральная функция правильная рациональная дробь. Знаменатель – многочлен n-ой степени может быть представлен в виде:

Q_n(x) =

Тогда, рациональную дробь можно представить в виде суммы простейших рациональных дробей.

R(x)=

В этом представлении A_i () и B_j () и С – неопределенные коэффициенты, которые можно найти следующим образом: приводим правую часть к общему знаменателю и после этого числитель правой части приравниваем к числителю левой части P_m(x). Этот метод называется методом неопределенных коэффициентов.

Пример 2: Вычислить

Решение.

1=

1. : 2. :

5.2. Интегрирование иррациональных функций

Пример 3: .

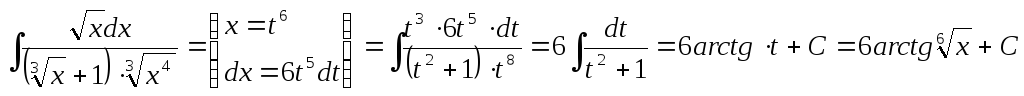5.3. Интегрирование тригонометрических функций

I. Интегралы вида (где R – рациональная функция) сводятся к интегралу от рациональной дроби путём универсальной подстановки:

,

, .

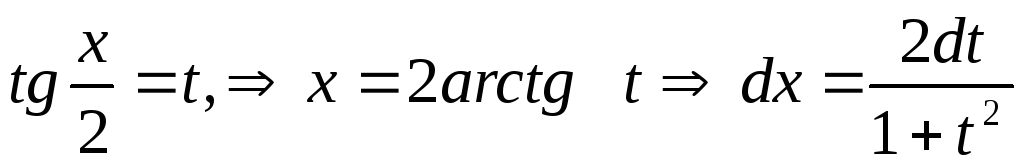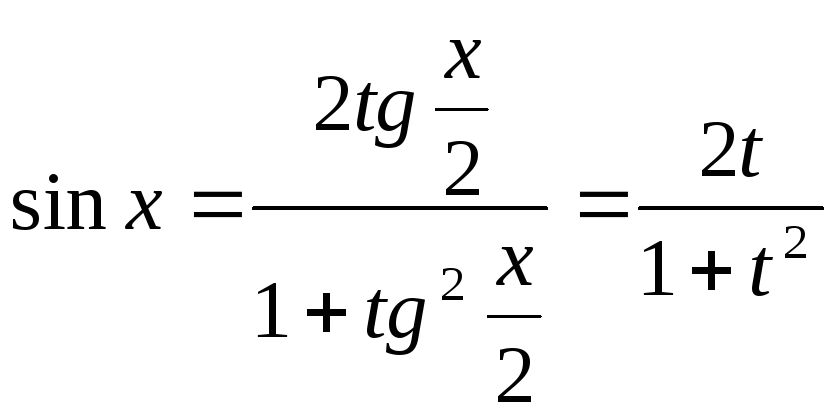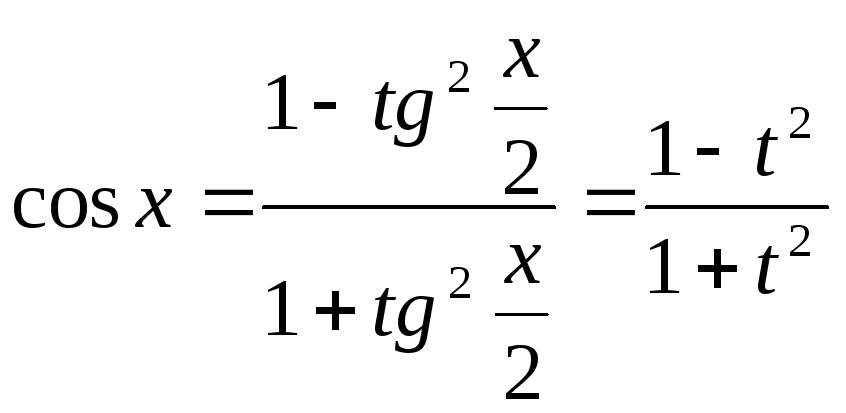Пример 4. .

II. , m, n – целые числа.

А) m – нечетное, тогда , если n – нечётное, то .

Б) m, n – четные, тогда применяем формулы понижения степени:

, .

Пример 5. а), б) .

III. , приводится к интегралу от рациональной дроби подстановкой

.

Пример 6. .

Замечание: Существуют неопределённые интегралы, которые не выражаются через элементарные функции:

- интеграл Пуассона - интегральный логарифм

- интеграл косинус - интеграл синус

- интеграл Френеля. , .

Тема 5. Определённый интеграл в.1. Формула Ньютона-Лейбница.

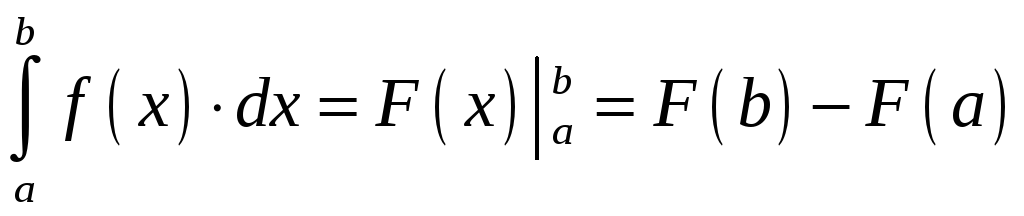
Пусть функция непрерывна не отрезке и любая первообразная функция на этом отрезке. Тогда определенный интеграл от функции на отрезке равен приращению первообразной на данном отрезке.

- приращение первообразной на данном отрезке

То есть нахождение определенного интеграла с помощью формулы Ньютона-Лейбница осуществляется в два этапа:

1. Используя технику нахождения неопределенного интеграла находим первообразную подынтегральной функции.

2. Вычисляем приращение первообразной на заданном отрезке.

Пример 1: