
- •Раздел. Математический анализ
- •Тема 1. Множества и функции в.1. Понятие множества
- •В.2. Абсолютная величина действительного числа. Окрестность точки
- •В.3. Определение функции
- •В.5. Элементарные функции
- •В.6. Интерполирование функций
- •В. 7. Преобразование графиков
- •Тема 2. Пределы и непрерывность в.1. Предел числовой последовательности
- •В.2. Предел функции
- •В. 3. Бесконечно малые величины
- •В. 4. Бесконечно большие величины
- •В. 5. Основные теоремы о пределах. Признаки существования предела
- •В. 6. Замечательные пределы
- •В.7. Непрерывность функции
- •В.8. Вычисление пределов
- •Тема 3. Дифференциальное исчисление функций одной переменной в.1. Задачи, приводящие к производной. Задача о касательной:
- •В.2. Определение производной функции
- •В.3. Основные правила дифференцирования
- •В.4. Производная сложной и обратной функций
- •В. 5. Производные основных элементарных функций
- •В.6. Производные высших порядков
- •В.7. Приложения производной
- •7.1. Правило Лопиталя
- •7.2. Возрастание и убывание функции. Экстремум функции
- •7.3. Исследование функции на выпуклость и точки перегиба
- •7.4. Асимптоты графика функции
- •9.4. Общая схема исследования функций и построения их графиков
- •В.8. Дифференциал функции
- •8.1. Определение дифференциала
- •8.2. Применение дифференциала в приближённых вычислениях
- •8.3. Дифференциалы высших порядков
- •Тема 4. Неопределенный интеграл (ни) в.1. Первообразная и неопределённый интеграл
- •В.3. Таблица ни
- •В.4. Методы интегрирования
- •4.1. Метод разложения
- •4.2. Метод замены переменной
- •4.3. Метод интегрирования по частям
- •В.5. Интегрирование отдельных классов функций
- •5.1. Интегрирование простейших рациональных дробей
- •5.2. Интегрирование иррациональных функций
- •5.3. Интегрирование тригонометрических функций
- •Тема 5. Определённый интеграл в.1. Формула Ньютона-Лейбница.
- •В.2. Замена переменной и интегрирование по частям в определенном интеграле.
В. 4. Бесконечно большие величины
Функция
f(x)
называется бесконечно
большой величиной
при х
х0,
если для M
> 0 найдется такое
> 0 (
(M)),
что для x
x0,
х
– x0
<
будет верно:
f(x
> M.
(Т.е.
![]() ).
).
Например,
функция
![]() - б.б.в. при х
0,
- б.б.в. при х
0,
![]() - б.б.в. при х
.
- б.б.в. при х
.
Замечание. Бесконечно большая величина есть функция неограниченная при х х0 (). В то же время не всякая неограниченная функция является бесконечно большой. Например, функция y = x sin x является неограниченной, но не бесконечно большой, т.к. с ростом х функция все время колеблется, переходя от положительных к отрицательным значениям и наоборот.
Свойства бесконечно больших величин:
-
Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.
-
Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.
-
Частное от деления бесконечно большой величины на функцию, имеющую предел в точке х0, есть величина бесконечно большая.
Связь между бесконечно малыми и бесконечно большими величинами устанавливает следующая теорема:
Теорема:
Если (x)
есть бесконечно малая при х
х0 (),
то функция f(x)
=
![]() является бесконечно большой при х
х0 ().
Обратно, если функция (x)
есть бесконечно большая при х
х0 (),
то функция f(x)
=
является бесконечно большой при х
х0 ().
Обратно, если функция (x)
есть бесконечно большая при х
х0 (),
то функция f(x)
=
![]() есть бесконечно малая при х
х0 ().
есть бесконечно малая при х
х0 ().
В. 5. Основные теоремы о пределах. Признаки существования предела
Пусть f(x) и (x) – функции, для которых существуют пределы при х х0 ():
![]() ,
,
![]() .
.
Тогда имеют место следующие теоремы о пределах:
-
Функция не может иметь более одного предела.
-
Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций:
![]() .
.
-
Предел произведения конечного числа функций равен произведению пределов этих функций:
![]() .
.
В частности, постоянный множитель можно выносить за знак предела:
![]() .
.
-
Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю):
![]() (B
0)
(B
0)
-
Если
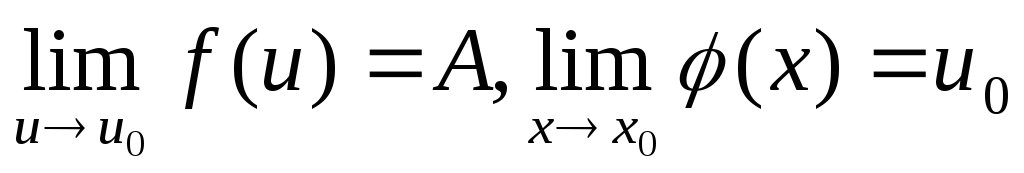 ,
то предел сложной функции:
,
то предел сложной функции:
![]() .
.
-
Если в некоторой окрестности точки х0 (или при достаточно больших х) f(x) < (x), то:
![]()
Использовать эти теоремы для выяснения существования предела не всегда удобно. Проще сделать это с помощью признаков существования предела:
Теорема 1. Если числовая последовательность {an} монотонна и ограничена, то она имеет предел.
Возможны два случая: а) последовательность неубывающая и ограничена сверху – a1 a2 a3 … an …M; б) последовательность невозрастающая и ограничена снизу – a1 a2 a3 … an …M;
Теорема 2. Если в некоторой окрестности точки х0 (или при достаточно больших х) функция f(x) заключена между двумя функциями φ(х) и (х), имеющими одинаковый предел А при х х0 (), то функция f(x) имеет тот же предел А.
В. 6. Замечательные пределы
Первым замечательным пределом является:
![]()
Вторым замечательным пределом является:
![]()
где е 2,718281…– число Эйлера, которое является основанием для натуральных логарифмов. Этот предел имеет записи:
![]() е
или
е
или ![]() е.
е.
Пример
2.
![]()
Для
раскрытия подобных неопределенностей
![]() используется первый замечательный
предел:
используется первый замечательный
предел: 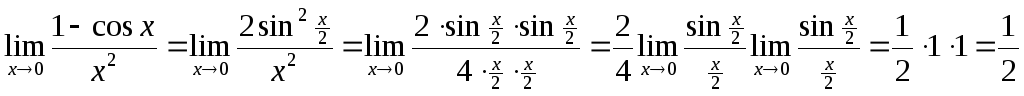
Пример
3.
![]()
Пример
4.
![]()
