2. Пуассоновські потоки подій і безперервні Марковські ланцюги.

Нехай система S із графом станів

у момент t перебуває в стані S_i і може перейти з нього в S_j під впливом пуассонівського потоку подій з інтенсивністю λ_ij. Як тільки з'являється перша подія цього потоку система переходить із S_i в S_j.

Імовірність такого переходу за проміжок часу ∆t дорівнює λ_ij∆t. Таким чином, щільність імовірності переходу λ_ij у безперервному ланцюзі Маркова являє собою інтенсивність потоку подій, що переводить систему зі стану в стан по відповідній стрілці.

Якщо всі потоки подій, що переводять систему S зі стану в стан, є пуассонівськими, то процес, що протікає в системі, буде Марковським.

Отже важливий висновок. Якщо розглядається система S, у якій переходи зі станів у стани відбуваються під дією пуассонівських потоків подій з певними інтенсивностями. Якщо поставити ці інтенсивності (щільність імовірностей переходів) на графі станів системи у відповідних стрілок, отримаємо розмічений граф станів системи. А, отже, для такої системи S можна відразу записати рівняння Колмогорова для ймовірностей стану.

Приклад: СКС складається із двох вузлів 1 і 2; кожний з них незалежно від іншого може відмовити. Потік відмов 1-го вузла – пуассонівський з інтенсивністю λ₁, другий пуассонівський з інтенсивністю λ_2.

Кожний вузол після відмови починає ремонтуватися. Потік відновлень для обох вузлів пуассонівський з інтенсивністю λ.

Граф системи:

S₁₁ – обидва вузли справні;

S₂₁ – перший ремонтується, другий справний;

S₁₂ – перший справний, другий ремонтується;

S₂₂ – обидва ремонтуються.

Позначивши ймовірності станів як P₁₁, P₁₂, P₂₁ і P₂₂, користуючись правилом запишемо рівняння Колмогорова як:

3. Граничні ймовірності станів.

Нехай є система S з дискретними станами

S₁, …, S_n ,

у якій протікає Марковський процес із безперервним часом.

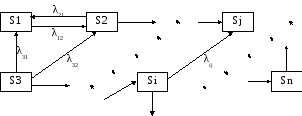
Припустимо, що всі інтенсивності потоків подій, що переводять систему зі стану в стан постійні, тобто λ _ij = const.

Т.т. потоки подій найпростіші (стаціонарні, пуассонівські потоки).

Якщо записати для системи рівняння Колмогорова й проінтегрувати їх при заданих початкових умовах, одержимо ймовірності станів як функції часу, тобто n функцій:

P₁(t), P₂(t), …, P_n(t),

При цьому для будь-якого t

_n

∑ P_i(t)=1

ⁱ⁼¹

Цікаво, що буде відбуватися із системою S якщо t ∞.

Чи будуть функції P₁(t), P₂(t), …, P_n(t) прагнути до деяких меж? Ці межі будуть називатися граничними ймовірностями станів.

У теорії ймовірностей доводиться наступне положення, яким ми скористаємося як готовим результатом.

Якщо число станів системи S кінцеве й з кожного стану можна перейти (за довільне число кроків) у кожне інше, то граничні ймовірності станів існують і не залежать від початкового стану системи.

На малюнку показаний граф, що задовольняє зазначеним умовам:

Очевидно, що для графа, наведеного нижче, ці умови нездійсненні. Отже для такого графа граничні ймовірності стану не існують.

Допустимо для деякої системи S умови виконуються й також імовірності існують, тобто

lim P_i(t)=P_i, (i=1,n)

^{t  ∞}

Очевидно, що граничні ймовірності стану P_i, як і P_i(t) повинні задовольняти умові

∑ P_i=1

ⁱ

Інакше кажучи, при t ∞ у системі S установлюється деякий граничний стаціонарний режим. Він полягає в тому, що система випадковим чином міняє свої стани, але ймовірність кожного з них уже не залежить від часу: кожний зі станів здійснюється з деякою постійною ймовірністю.

Який фізичний зміст такої ймовірності?

Вона являє собою не що інше, як середній відносний час перебування системи в цьому стані.

Наприклад: нехай система S має 3 стани S₁, S₂, S₃. Відповідно граничні ймовірності станів рівні 02, 03, 05. Це означає, що в сталому режимі система S у середньому 0,2 часу буде перебувати в стані S₁, 0,3 у стані S₂ і 0,5 часу в стані S₃.

Як же обчислити граничні ймовірності стану.

Знову скористаємося готовим результатом теорії ймовірностей: для обчислення граничних імовірностей стану системи S, що задовольняє відповідним умовам їхнього існування, потрібно записати рівняння Колмогорова й покласти всі ліві частини (похідні від P_i(t)) рівними нулю.

Дійсно, у граничному (сталому режимі) всі ймовірності станів постійні, а виходить, їхні похідні дорівнюють нулю.

Якщо всі ліві частини рівнянь Колмогорова покласти рівними нулю, то система лінійних диференціальних рівнянь перетвориться в систему лінійних алгебраїчних рівнянь. При цьому одне з них, може бути замінено виразом з умови нормування

∑ P_i=1

ⁱ

Приклад:даний розмічений граф станів

Рівняння Колмогорова мають вигляд:

або для граничних імовірностей стану:

0=-5P₁+P₃

0=-P₂+2P₁+2P₃

0=-3P₃+3P₁+2P₄

0=-2P₄+P₂

Останні рівняння, як відомо з лінійної алгебри, визначають величини P_i з точністю до постійного множника. Тому для точного визначення значень граничних імовірностей стан додаткового варто скористатися умовою нормування

P₁+P₂+P₃+P₄=1

Для цього виразимо, наприклад, всі невідомі ймовірності через одну з них, нехай через P₁

Тоді

P₃=5P₁

Підставляючи в 2-е рівняння одержимо:

P₂=2P₁+2P₃=2P₁+10P₁=12P₁

Четверте рівняння дасть

P₄=0,5P 2-₆P₁

Отже (з урахуванням,що умови нормовані)

P₁+12P₁+5P₁+6P₁=1;

і 24P₁=1;

P₁=1/24, P₂=12P₁=0,5, P₃=5P₁=5/24, P₄=6P₁=0,25

Це значить, що в сталому режимі система S у стані S₁ буде перебувати 1/24 часу, у стані S₂ – половину часу, у стані S₃ – 5/24 часу й у стані S₄ – 0,25 часу.

Помітимо наступне. Ми спочатку записували в розглянутому прикладі систему рівнянь Колмогорова, а потім переходили до системи лінійних алгебраїчних рівнянь.

На практиці при дослідженні систем можна безпосередньо відразу складати систему лінійних алгебраїчних рівнянь, минаючи перший етап. При цьому щоб не помилятися зі знаками, всі члени рівнянь, що відповідають вихідним стрілкам, записувати в лівій частині рівності, а вхідним - у правій частині.

Дійсно:

5P₁=P₃

P₂=P₁+2P₃

3P₃=3P₁+2P₄

2P₄=P₂

₄

∑ P_i=1

ⁱ⁼¹

Тепер відзначимо одну дуже цікаву обставину. Якщо кілька безперервних ланцюгів Маркова мають однакові структури графів станів і відрізняються тільки значеннями інтенсивностей λ_ij, то немає необхідності знаходити граничні ймовірності станів для кожного із графів шляхом рішення щораз нової системи рівнянь. Досить один раз скласти й вирішити в загальному (буквеному) виді рівняння для такого графа, а потім підставити значення λ_ij для кожного конкретного випадку у відповідні вирази.