2. Висновки

Становить інтерес вивчити залежності від кількості джерел m і величини , де під  у цьому випадку розуміється =(+)

І зрівняти ці дані з даними, отриманими для марковської моделі завдання про простій верстатів.

Як показують експерименти при 0.11.0 и /0,2 відмінності величини ( для цих двох моделей становлять не більше 5-6% у широкому діапазоні зміни m.

14. Лекція 14. Вкладені ланцюги Маркова

План лекції

1. Метод вкладених ланцюгів Маркова.

2. Задача простою верстатів.

1. Метод вкладених ланцюгів Маркова

На розглянутих прикладах ми бачимо, що, якщо час обслуговування відрізняється від показового закону, то відповідний випадковий процес втрачає марківську властивість і одержати шукані результати найпростішими методами не завжди вдається й доводиться задовольнятися деякими приблизними результатами.

Для подолання труднощів, що виникли познайомимося ще з одним методом дослідження характеристик СМО, що певною мірою допомагає перебороти їх.

Якщо розглядати випадковий процес у СМО лише в ті моменти часу, коли чергова процедура обслуговування виявилася тільки що завершеною й відповідна вимога саме залишає систему кажучи, що ми розглядаємо процес у точках регенерації (або точках відновлення ). У цьому випадку для пророкування наступної еволюції системи потрібно лише вказати кількість вимог, що перебувають у такі моменти усередині обслуговуючої системи й немає необхідності в докладному знайомстві з перед історією процесів у наступній системі.

Тому ймовірність поводження системи в таких регенерації може бути описана за допомогою так званих вкладених ланцюгів Маркова. Поняття «вкладені» показує тут та обставина, що стани системи розглядаються тільки в момент регенерації, у яких випадковий процес володіє марковською властивістю.

Будемо вважати , що n - число вимог, що перебувають у системі відразу ж після завершення чергової процедури обслуговування( у деякий момент часу Т), а n' - число вимог відразу після завершення наступної одна за одною процедури обслуговування (у момент часу Т'). нехай j число надходжень в інтервалі(Т,Т').

Тодіj, якщо n=0

n` = n- 1+j, якщо n>0 (1)

якщо Т'-Т=h, то

Z [ j надходжень| інтервал (Т,Т+h)] =

За умови, що вхідний потік пуассоновський з параметром .

Отже безумовно ймовірність надходження j вимог

(2)

тут G(h) – функція розподілу тривалоситей процедур обслуговування.

Для деяких G(h) величини k_j легко можна обчислити. У ряді випадків , це досить важко. Тоді вдаються до чисельних методів інтегрування.

Але для початку навчимося будувати вкладений Марковський ланцюг.

Стан вкладеного ланцюга Маркова характеризуються числом вимог у системі в момент регенерації. Отже, при заданій n імовірність виявлення в системі n' вимог задовольняє умові (1) і визначається ймовірністю j надходжень, заданою співвідношенням(2).

Шуканий марковський ланцюг може бути записаний у вигляді наступної матриці

2. Задача простою верстатів

Розглядаючи на конкретному прикладі завдання про простій верстатів з постійним часом обслуговування, побудуємо вкладений ланцюг маркова:

Розглянемо цей ланцюг у момент регенерації t, t+, t+2, t+3, … , t+i, де t може бути будь-яким, зокрема t=0, а =t_обсл.=1/=const.

Якщо в деякий момент часу Т у системі перебуває j вимог на обслуговування , то до моменту Т+ одна вимога буде обслужена й кількість вимог у системі стане рівним I= j-1+n_m-j, де nm-j – число надходжень від m джерел протягом інтервалу {Т,Т+}.

У результаті одержимо наступну матрицю для марківських переходів , що описує стан системи в момент часу, розділені інтервалами тривалістю .

Позначимо через імовірність надходження j вимог від i джерел за час, що для =const визначається як

	0	1	2	…	m-1	M
0				…
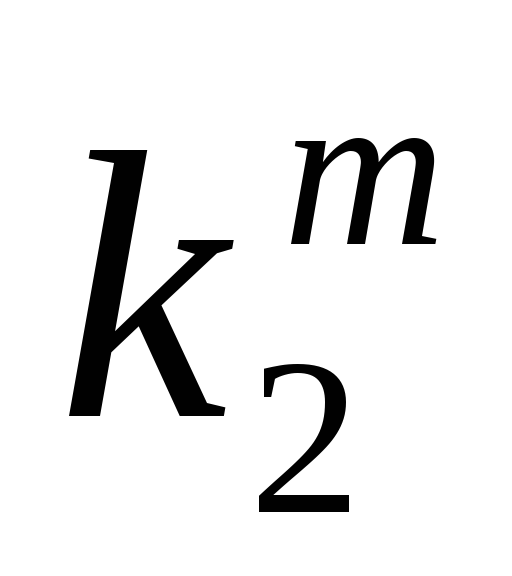
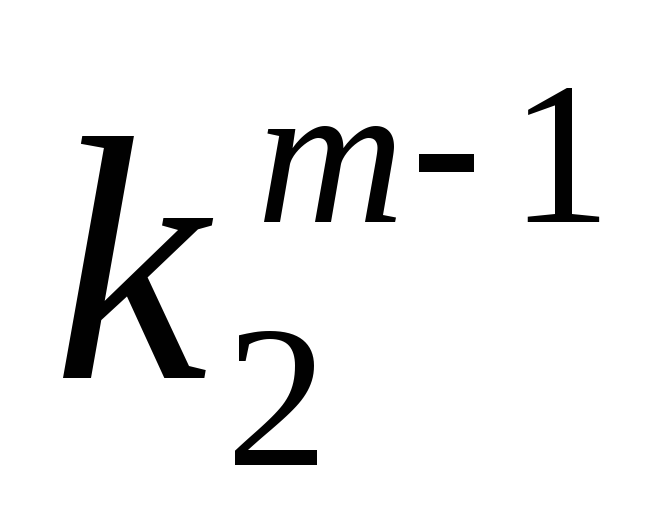
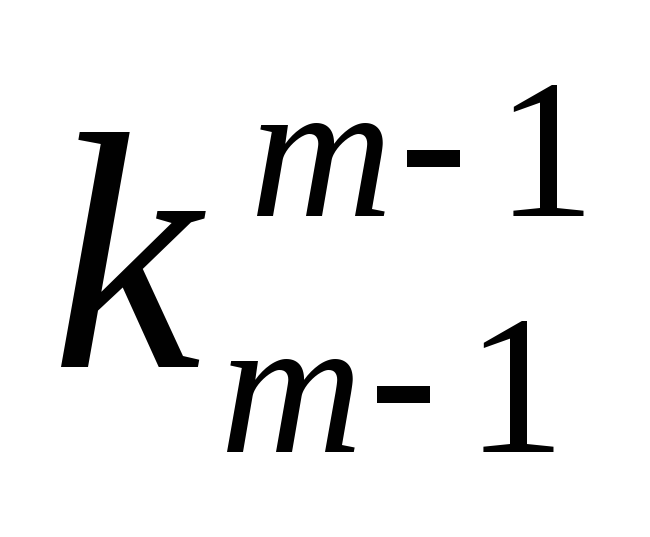
1				…		0
2	0			…		0
3	0	0		…		0
…	0	0	0	…	…	0
m-1	0	0	0	…		0
m	0	0	0	…		0

Відповідно до наведеної матриці:

рівняння , задане першою рівністю системи можна замінити рекурентним співвідношенням

Цікава імовірність Z₀ може бути визначена з наступних міркувань, нехай відома деяка величина

Тоді, використовуємо співвідношення (1) можна обчислити всі значення

а для визначення значення q₀ скористатися співвідношенням

звідки:

Поставимо запитання , чи збігаються значення граничних імовірностей стану для вкладеного марківський ланцюга із граничними ймовірностями і стану досліджуваної не-марківської моделі.

Адже у випадку вкладеного ланцюга ми розглядаємо довжину черги заявок лише в момент часу t_k(k=1,2,…),коли вимоги залишають систему.

Очевидно, що множина {n (t_k), k=1,2,…}є підмножиною множини {n(t), tТ_g}, де Т_g – множина всіх точок дійсної прямої й межу

У загальному випадку не обов'язково повинен збігатися з межею

В цитуємій книзі: Джейсун Р. « Черги із пріоритетами», М., «Мир»,1973р.; доведено , що це дійсно так для моделей з кінцевими джерелами й для моделей із пріоритетами.

Звідси витікає, що граничні ймовірності стану системи Р_j для цього класу моделей Р_jZ_j ; зокрема й Р₀Z₀ .

Для ланцюгів практики необхідно з'ясувати наскільки велика ця розбіжність.

Тому спробуємо описати формули за допомогою, яких можна було б від множини значень Z_j перейти до шуканої множини Р_j.

Із цією метою можна скористатися результатами ергодичної теореми для процесів з дискретним втручанням випадку, доказ якої наведено в книзі: Гіхман И.И., Скороходов А.В. «Теорема випадкових процесів», том 2, М., «Наука»,1973р.

Використовуючи цю теорему , стосовно до нашої проблеми, можна записати наступне співвідношення:

Q_ik(t)- розподіл числа вимог n(t) у момент часу t за умови, що при t=0, n(t)=I,

A_m – константа, що витісняється з умови нормування  P_k=1.

Якщо розглядати стан вкладеного марківського ланцюга в момент часу t_k , що безпосередньо випливають за тим , як обслужені вимоги вертаються в джерело, вираз (1) можна переписати як

Де

Можна показати, що при k=0,

А при k>0

Приймаючи це до уваги, остаточно для формул перерахування одержимо:

Де

Стосовно до нашого випадку завдання про простій верстатів з постійним часом обслуговування вираз (1) прийме вигляд

Або з урахуванням (2)

Або розкладаючи ( 1-е^-t) k-^I, і виконуючи нескладні перетворення одержимо:

Звідки остаточно формула перерахування прийме вид:

Порівняння залежностей ((m), m - число джерел для різних значень величини  з урахуванням формул перерахування й без них показує, що максимальна погрішність результату лежить у межах 5-10% у широкій області зміни параметрів.

Тому на практиці цілком можна обмежиться обчисленням значень граничних імовірностей стану Р_кZ_к для розглянутого класу моделей.

Дуже часто в наукових публікаціях при дослідженні різних не-марковських моделей СМО використовується апарат вкладених ланцюгів Маркова. При цьому не звертається належної уваги на оцінку можливих погрішностей. Тому при запозиченні таких результатів при практичному використанні варто звернути увагу на величини можливих помилок обчислення для кожної конкретної моделі СМО.