2. Випадкові процеси з дискретним і безперервним часом. Марківський ланцюг

Випадковий процес називається процесом з дискретним часом, якщо переходи системи зі стану в стан можливі тільки в строго певні, заздалегідь фіксовані моменти часу: t₁, t₂, ... У проміжках часу між цими моментами система S зберігає свій стан.

Випадковий процес називається процесом з безперервним часом, якщо перехід системи зі стану в стан можливий у кожній, наперед невідомий, випадковий момент часу. Спочатку розглянемо марківський процес із дискретними станами й дискретним часом.

Нехай фізична система S може перебувати в станах:

S_1, S_{2, …} S_{n ,}

Причому переходи зі стану в стан можливі тільки в моменти часу:

t_1, t_{2, …} t_{k , …}

будемо називати ці моменти «кроками» або «етапами» процесу й розглядати випадковий процес як функцію цілочисельного аргументу:

1, 2, ... , k, ... (номер кроку).

Випадковий процес полягає в тому, що в послідовні моменти часу t_1, t_2,…система S виявляється в тих або інших станах :

S₁ -> S₃ -> S₅ -> S₄ -> S₂ -> ...

У загальному випадку система може в моменти часу t_1, t_{2, …} t_k не тільки міняти стан, але й залишатися в колишньому, наприклад:

S₁ -> S₁ -> S₂ -> S₃ -> S₃ -> S₃ -> S₄ -> …

Умовимося позначати S_і^(k) подія, що складається в тому, що після k кроків система перебуває в стані S_{і .}

Процес, що відбувається в системі, можна представити як послідовність (ланцюжок) подій, наприклад:

S₁⁽⁰⁾ , S₂⁽¹⁾ , S₁⁽²⁾ , S₂⁽³⁾ , S₃⁽⁴⁾ , ...

Така випадкова послідовність подій називається Марковським ланцюгом, якщо для кожного кроку ймовірність переходу з будь-якого стану в S_і в будь-який стан S_j не залежить від того, коли і як система прийшла в стан S_і.

Будемо описувати марковський ланцюг за допомогою так званих імовірностей станів.

Нехай у будь-який момент часу, після будь-якого k-го кроку система S може перебувати в одному зі станів :

S_1, S_{2, …} S_n ,

т.е. здійсниться одне з повної групи несумісних подій :

S₁^(k) , S₂^(k) , … , S_n ^(k) ,

Позначимо ймовірності цих подій :

Р₁(1) = Р(S₁⁽¹⁾ ) ; Р₂(1) = Р(S₂⁽¹⁾ ); ... ; Р_n (1) = Р(S_n ⁽¹⁾ ). - імовірності після першого кроку,

Р₁(2) = Р(S₁⁽²⁾ ) ; Р₂(2) = Р(S₂⁽²⁾ ); ... ; Р_n (2) = Р(S_n ⁽²⁾ ) – імовірності після другого кроку,

і, взагалі, після k-го кроку:

Р₁(k) = Р(S₁^{(k )} ) ; Р₂(k) = Р(S₂^(k) ); ... ; Р_n (k) = Р(S_n ^(k) )

Легко бачити, що для кожного номера кроку k

Р₁(k) + Р₂(k) + …....+ Р_n (k) = 1,

оскільки це ймовірності несумісних подій, що утворять повну групу.

Будемо називати ймовірності

Р₁(k) , Р₂(k) , …...., Р_n (k) – імовірності станів.

Поставимо завдання: знайти ймовірності станів системи для будь-якого k .

Представимо стани системи S у вигляді графа, де стрілками зазначені можливі переходи системи зі стану в стан крок за кроком.

2-й крок

Випадковий процес можна уявити собі так, нібито якась крапка, що зображує систему S випадковим образом, переміщається по графі зі стану в моменти часу t₁ , t₂ , …..., а тоді й затримується (у загальному випадку) на якесь число кроків у певному стані.

Наприклад: наступна послідовність переходів :

S₁ -> S₃ -> S₂ -> S₂ -> S₃ -> S₅ -> S₆ -> S₇ ->

Для будь-якого кроку (моментів часу t₁ , t₂ , …..., t_к ….... або номера 1,2,... k ).

Існують якісь імовірності переходу з будь-якого стану в будь-який інший (при цьому деякі із цих імовірностей дорівнюють нулю, або безпосередній перехід за один крок неможливий, що відповідає графові), а також імовірності затримки системи в даному стані.

Будемо називати ці ймовірності перехідними ймовірностями Марковського ланцюга.

Марковський ланцюг називається однорідним, якщо перехідні ймовірності не залежать від номера кроку. У противному випадку ланцюг називається неоднорідним.

Нехай система S має n можливих станів. Нехай нам також відомі для кожного стану ймовірності переходу в будь-який інший стан за 1 крок (у т. числі й імовірність затримки в даному стані).

Позначимо Р_ij імовірність переходу за один крок зі стану S_i у стан S_j. Р_ii – імовірність затримки системи в стані S_i.

Ці ймовірності можна записати у вигляді матриці:

|

Деякі з імовірностей Р_ij можуть дорівнювати нулю.

Суми ймовірностей у кожному рядку наведеної матриці рівні 1, тому що в якому би стані система не була перед k-м кроком, події S₁^(k) , S₂^(k) , … , S_n ^(k) несумістні й утворять повну групу.

При розгляді Марковських ланцюгів буває зручно користуватися графом станів, на якому біля стрілок переходів проставлені відповідні перехідні ймовірності.

Імовірності «затримки» у стані проставляти зайво, хоча й можна це робити, тому що кожна з них доповнює до 1 суму перехідних імовірностей.

Для наведеного графа:

Р₁₁ = 1- (Р₁₂ +Р₁₃)

Р₂₂ = 1- (Р₂₃ +Р₂₄)

Р₃₃ = 1- (Р₃₂ +Р₃₅)

Р₄₄ = 1- (Р₄₃+Р₄₅ +Р₄₆)

Р₅₅ = 1- Р₅₆

Р₆₆ = 1- Р_62.

Якщо зі стану S_i не виходить ні однієї стрілки, відповідна ймовірність затримки Р_ii дорівнює одиниці.

Маючи розмічений граф (або матрицю перехідних імовірностей) і знаючи початковий стан системи, можна знайти ймовірності станів:

Р₁(k) , Р₂(k) , …...., Р_n (k)

після будь-якого k-го кроку.

Нехай у початковий момент (перед 1-м кроком) система перебуває в деякому стані S_m .

Тоді для початкового моменту будемо мати:

Р₁(0)=0 , Р₂(0)=0 , …, P_m (0)=1, ....., Р_n (0)=0

Знайдемо ймовірності станів після першого кроку. Оскільки система перебувала в стані S_m, то в стани

S_1, S_{2, …,} S_m, … S_n вона перейде з імовірностями

P_m1, P_{m2, …} P_{mn, …} P_mn

Отже, імовірності станів після 1-го кроку будуть:

Р₁(1) = P_m1, Р₂(1) = P_m2, …, P_m (1)=P_mm, ....., Р _n (1) = P_m

Знайдемо ймовірність після другого кроку:

Р₁(2) , Р₂(2) , … Р_i(2), ..., Р_n (2)

Будемо їх витісняти по формулі повної ймовірності з гіпотезами:

----------------після першого кроку система була в стані S₁

------ ---- --- ---- --- ---- --- ---- --- ---- --- ---- --- ---- --S₂

…………………………………………………………….S_i

---- ----- ---- ---- ----- ---- --- ---- --- ---- --- ---- --- --- --S_n

Імовірності гіпотез Р₁(1) , Р₂(1) , …...., Р_n (1) відомі. Вони витиснуті на першому кроці. Тоді одержимо:

Р₁(2) = Р₁(1) Р₁₁ + Р₂ (1) Р₂₁ + ... + Р_n (1) Р_n1 ;

Р₂(2) = Р₁(1) Р₁₂ + Р₂ (1) Р₂₂ + ... + Р_n (1) Р_n2 ;

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Р_i (2) = Р₂(1) Р_1i + Р₂ (1) Р_2i + ... + Р_n (1) Р_ni ;

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Р_n (2) = Р₁(1) Р_1n + Р₂ (1) Р_2n + ... + Р_n (1) Р_nn ;

Або _{n ――}

P_i(2)= ∑ P_j(1)P_ji, (i=1,n)

^j=1

Т.ч імовірності після 2-го числа відомі, після 3-го;

_n

P_i(3)=∑P_j(2)P_ji;

^j=1

і взагалі, після k-го кроку;

_n

P_i(k)=∑P_j( k-1)P_ji, (i=1,n)

^j=1

т.т. розрахунок можна виконати по цій рекурентній формулі для P_i(k).

Приклад:

Є буфер з 3-ма осередками, стан якого проглядається через рівні фіксовані проміжки часу: t1, t2, t3, t4 ...

Визначити стан буфера в момент t4.

Si - буфер порожній

S2 - зайнятий один осередок за ∆t

S3 - зайнято 2 осередка за всі ∆t

S4 - буфер повністю заповнений

Граф станів S наведений нижче:

P₁(4)=0,008

P₂(4)=0,070

P₃(4)=0,129

P₄(4)=0,793

Марковський процес із дискретними станами й безперервним часом.

На практиці часто зустрічаються ситуації, коли переходи в системі відбуваються не у фіксовані, а у випадкові моменти часу, які заздалегідь указати неможливо.

Такі процеси часто можна описати за допомогою Марковського випадкового процесу з дискретними станами й безперервним часом, тобто безперервним ланцюгом Маркова.

Покажемо, як виражаються ймовірності станів для такого процесу.

Нехай є ряд дискретних станів:

S₁, S, …, S_n

Перехід зі стану в стан може здійснюватися в будь-який момент часу.

Позначимо P_i(t) – імовірність того, що в момент t система буде перебувати в стані S_i, (i=1, n). Очевидно, що для будь-якого моменту t сума ймовірностей дорівнює одиниці,

Т.т. _n

∑ P_i(t)=1

ⁱ

Визначимо для будь-якого t імовірності станів

P₁(t), P₂(t), …, P_n(t)

Для цього потрібно знать характеристики процесу, аналогічні перехідним імовірностям для Марковського ланцюга.

У випадку процесу з безперервним часом, імовірність переходу зі стану в стан, точно в момент часу t завжди дорівнює 0. Тому замість перехідних імовірностей P_ij введемо в розгляд щільності ймовірностей переходу λ_ij.

Під нею будемо розуміти межу відношення ймовірності переходу системи за час ∆t зі стану S_i у стан S_j до довжини проміжку ∆t:

P_ij(∆t)

λ_ij=lim———

^∆t0 ∆t

Тут P_ij(∆t) – імовірність того, що система зі стану S_i перейде в стан S_j за час ∆t.

З виразу для λ_ij з точністю до нескінченно малих вищих порядків випливає, що

P_ij(∆t)≈ λ_ij∆t

Якщо вага точності ймовірностей переходу λ_ij не залежить від t (тобто від того, коли елементарна ділянка ∆t), Марковский процес називається однорідним, а якщо вони представляють якісь функції від часу λ_ij(t) – процеси називаються неоднорідним.

Відповідно будемо розрізняти однорідні й неоднорідні ланцюги.

Якщо нам відомі щільності ймовірності λ_ij для всіх пар ij, то можна побудувати так званий розмічений граф станів, проставивши біля кожної стрілки значення λ_ij

Виявляється, що ймовірності станів P₁(t), P₂(t), …, P_n(t) можна також визначити, тому що вони задовольняють певного виду диференціальним рівнянням. Ці рівняння називаються рівняннями Колмогорова.

Для початку поставимо завдання: знайти ймовірність P₁(t), тобто ймовірність того, що в момент t+∆t система буде перебувати в стані S₁.

Така подія може відбутися двома способами:

- у момент t система вже була у стані S₁, а за час ∆t з нього вже вийшла;

- у момент t система була в стані S₃ (див. розмічений граф), а за час ∆t перейшла з нього в стан S₁.

Імовірність першого варіанта знайдемо як добуток імовірностей P₁(t), що в момент t система була у стані S₁, на умовну ймовірність того, що будучи у стані S₁, система за час ∆t не перейде з нього в S₂. Ця умовна ймовірність (з точністю до нескінченно малих вищих порядків) дорівнює 1- λ₁₂∆t.

Імовірність другого варіанту дорівнює ймовірності того, що в момент t система була у стані S₃, помноженої на умовну ймовірність переходу за час ∆t у стан S:

P₃(t) * λ₃₁∆t

Застосовуючи правило додавання ймовірностей одержимо:

P₁(t+∆t)=P₁(t)( 1-1- λ₁₂∆t)+P₃(t) λ₃₁∆t

Розкриємо дужки в правій частині, перенесемо P₁(t) у ліву частину й розділимо обидві частини рівняння на ∆t:

Спрямуємо ∆t  0 і перейдемо до межі

Ліва частина не що інше, як похідна функції P₁(t), тобто

Аналогічні рівняння можуть бути отримані для P₂(t), P₃(t) і P₄(t).

Міркуючи аналогічно, одержимо в результаті систему рівнянь:

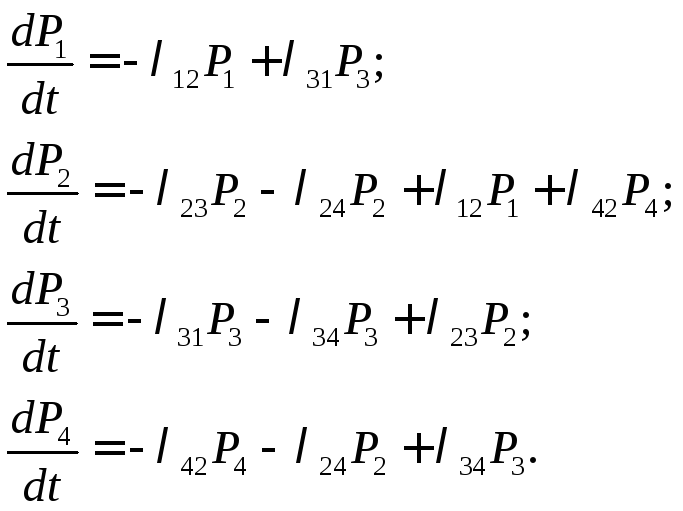
Ці рівняння називається рівняннями Колмогорова.

Інтегрування цих рівнянь і дає потрібний результат. Початкові умови беруться залежно від того, яким був початковий стан системи S.

Наприклад, якщо при t=0, P₁=1, то P₂= P₃= P₄=0

У системі одне з рівнянь є зайвим тому що

P₁+ P₂+ P₃+ P₄≡1

і, скажімо, 4-те рівняння може бути замінене на

P₄= 1-1-( P₁+ P₂+ P₃)

Цікавим є те, що побудова системи рівнянь підпорядковується формально певному правилу, що істотно спрощує складання системи рівнянь.

Правило: У лівій частині кожного рівняння знаходиться похідна ймовірності стану, а права частина містить стільки членів, скільки стрілок пов'язане з даним станом. Якщо стрілка спрямована зі стану, відповідний член має знак «мінус», якщо в стан – знак «плюс». Кожний член дорівнює добутку точності ймовірності переходу, що відповідає даній стрілці, помноженої на ймовірність того стану, з якого виходить стрілка.

Це правило є загальним і справедливо для будь-якої безперервної Марковського ланцюга. Системи рівнянь можна записувати чисто механічно.

Наприклад, розмічений граф станів має вигляд.

Написати систему рівнянь Колмогорова, якщо система в початковий момент перебуває в стані S₁

Початкові умови:

при t=0, P₁=1, P₂= P₃= P₄= P₅=0