Контрольні запитання

1. Які властивості марківського випадкового процесу.

2. Який випадковий процес називають випадковим процесом з дискретними станами та дискретним часом.

3. Який випадковий процес називають випадковим процесом з дискретними станами і безперервним часом.

4. Які імовірності називають перехідними ймовірностями марківського ланцюга.

5. Яка різниця між однорідними та неоднорідними марківськими ланцюгами.

6. Яка існує формула для визначення ймовірностей станів після декількох кроків переходів для випадкового процесу з дискретними станами і часом.

7. Яке існує правило для визначення рівнянь Колмогорова за розміченим графом станів випадкового процесу

Рекомендована література

1. Е.С. Вентцель. Исследование операций. «Сов. радио» М., 1972.

3, Лекція 3 .Математична модель для оцінки часу виконання програми

Вступ. Програмне забезпечення (П3) спеціалізованих комп’ютерних систем має ряд особливостей, серед яких: вирішення завдань у реальному часі; незмінність функцій П3 під час усього періоду експлуатації; необхідність обміну інформацією із зовнішнім абонентом.

Це вже на стадії проектування П3 [1] потребує виконати його оптимізацію та оцінити часові характеристики програм: середній час виконання; середню частоту виконання окремих блоків; перевірити можливість зациклювань і т.п. На даний час існує декілька підходів до вирішення цих задач: створення декількох варіантів програмної системи і на основі реальних даних обрати оптимальний варіант; імітаційне моделювання; створення і дослідження математичних моделей. Перший підхід може виявитися дуже затратним та неприпустимим у часі розробки. Другий, хоча і дозволяє у найменших деталях відтворити процеси функціонування П3, у більшості випадків не може бути рекомендований на ранніх стадіях проектування, оскільки не можна точно визначити вхідні параметри моделей і розрахувати відповідні навантаження окремих блоків обчислюваної системи. Отже, створення і дослідження математичних моделей функціонування П3 є дуже перспективним підходом.

Постановка задачі.Метою роботи є створення математичної моделі функціонування П3, за допомогою якої можна оцінювати такі характеристики програми (комплексу програм) як: відсутність можливості зациклювання; середній час виконання; середня частота виконання окремих блоків.

Опис математичної моделі.Поставимо у відповідність блок-схемі алгоритму програми орієнтований граф , у якому вершини будуть співставленні блокам і розгалуженням, а орієнтованим ребрам-шляхи переходу алгоритму між окремими блоками. Будемо вважати, що процесу виконання програми будуть відповідати переходи з однієї вершини до іншої, а знаходженню у певній вершині – виконанню деякої команди або блоку програми. У якості прикладу на рис.1а наведено блок-схему алгоритму програми пошуку максимального елементу в одномірному масиві, а на рис. 1б-відповідний граф .

а) б)

Рис.1 Блок-схема алгоритму програми та можлива її інтерпретація

графом .

Зауважимо, що граф може бути побудований для алгоритмів будь-якого рівня: рівень команд, модулів,процедур,операторів мови проектування програмPDL[1] і т.п. Використовуючи таку модель, можна розглядати виконання програми як існування деякого випадкового процесу з дискретними станами і з дискретним або неперервним часом, якому відповідає граф . Зважаючи на особливості виконання програм, можна вважати, що переходи процесу із стану в стан, не залежить від того, яким чином він потрапив у стан , а тільки залежить від перехідних імовірностей , якими навантажують (розмічають) відповідні ребра графа .

З урахуванням цього, можна інтерпретувати процес виконання програми як випадковий марківский процес з дискретними станами, які пов’язані у марківський ланцюг матрицею перехідних імовірностей .

Нагадуємо, що випадковий процес , який відбувається у системі, зветься процесом з дискретним часом, якщо перехід з одного стану в інший відбувається тільки у попередньо визначені моменти часу що звуться кроками такого процесу. У проміжках між кроками система зберігає свій стан. При цьому не виключається, що на деяких кроках система не буде змінювати свій стан. Як відомо [2], випадковий процес з дискретним часом

можна представити випадковою послідовністю (по індексу) таких подій

; (1)

де – кількість вершин графа .

Оскільки система у довільний момент часу може перебувати тільки в одному із станів, то при кожному події несумісні і утворюють повну групу подій. Основними характеристиками марківських

ланцюгів з дискретним часом є імовірність станів

, ;

та імовірності переходів, що утворюють квадратну матрицю переходів порядку .

(2)

(3)

(4)

Наявність на розміченому графі стрілок та визначень відповідних імовірностей переходів вказує на відмінність їх від нуля. Відсутність стрілок говорить про те, що відповідні імовірності дорівнюють нулю. Якщо сума імовірностей, що виходять з певної вершини <1, це свідчить про імовірність затримки на певному кроці, яка дорівнює

(5)

Якщо, це свідчить про те, що процес потрапив в так званий поглинаючий стан, з якого він вже вийти не може, блукання по станам завершується. Вектор-строка станів у початковий момент дискретного часу

зветься вектором початкового розподілення імовірностей. Для наведеного прикладу (малюнок 1Б)він дорівнює. Як відомо [3], для визначення вектору-строки імовірностей переходу від кроку до кроку слід взяти добуток вектору-строки переходу від стану до на матрицю перехідних імовірностей , тобто

, (6)

у загальному вигляді

або [2] (7)

Яким же чином визначити імовірності переходу. Вони визначаються шляхом аналізу операторів переходу та циклів , що впливають на шляхи очислювального процесу. Наприклад, якщо імовірність виконання умови в операторі переходу дорівнює 0,3, то двом шляхам розвитку обчислювального процесу відповідають імовірності 0,3 та 0,7. Якщо цикл повторюється у середньому 10 разів, то імовірність виходу із циклу становить 0,1 а виходу із циклу – 0,9.

Як правило, дискретність моментів переходу розглядається як стала величина, тобто, . Ми, дещо, розширимо поняття дискретності моменту переходу і пов’яжемо його з попереднім станом процесу. Будемо вважати, що якщо процес переходить із стану в стан, то такий перехід можливий після завершення проміжку часу τ_iзнаходження процесу у стані . Власне кажучи, ми у такому разі, розглядаємо випадковий процес з дискретним часом, у якого переходи відбуваються через попередньо визначені, але нерівномірні інтервали часу, тобто з нерівномірною дискретизацією часу.

Визначимо величину проміжку часу між сусідніми кроками. Ця величина буде дорівнювати

, (8)

або буде відповідати рівнянню

(9)

при нерівномірній дискретизації та при рівномірній дискретизації. Якщо

, (10)

що збігається з результатом (3).

Якщо кроки нерівномірні за часом, то величина визначається за формулою (9) і буде залежатиме від.

Кожний алгоритм або програма, як правило, мають початок і кінець. Таким чином, ця необхідна умова відповідає структурі графа . Як відомо [3], перетворюючи алгоритм або програму у граф , можна попередньо побудувати діаграму порядку, оскільки вона представляє собою граф без контурів. При цьому, у графі можуть існувати тупікові вершини – вершини, з яких дуги не виходять за межі контуру. Підграфи, що відповідають тупіковим вершинам, звуться ергодичними класами марківського ланцюга. Якщо ергодичний клас складається з однієї вершини, то такий стан називається поглинаючим. Наприклад, на рис. 2 наведено граф та його діаграма порядку.

(а) (б)

Рис.2 Граф переходів – а, та його діаграма порядку – б

Згідно діаграми порядку видно, що у графі існує два ергодичні класи:

Клас є поглинаючим.

Під час блукання по графу з імовірністю 1, траєкторія марківського ланцюга опиниться в одному з ергодичних класів і вийти з нього не зможе. Якщо наведений граф відповідає деякий конкретній програмі, то можна казати, що початку програми відповідає вершина 1, кінцю - вершина 8, ергодичний клас відповідає похибці – «зациклюванню» програми, яка має бути виправлена, а – поглинаючий.

Метод використання моделі програми. За допомогою моделі програми у вигляді поглинаючого марківського ланцюга можна обчислити кількість звертань до окремих блоків програми, середній час виконання програми, середню кількість кроків до переходу у поглинаючий стан, що свідчить про завершення програми. Ці характеристики програм можна у подальшому використовувати для застосування методів профілювання коду. Як відомо, для визначення вказаних характеристик програм застосовувались методи імітаційного моделювання [4] і метод, заснований на побудові фундаментальної матриці, кожний з елементів якої дорівнює середній кількості раз попадання системи в той чи інший стан до поглинання [4]. Обидва методи досить складні у реалізації та мають проблеми із пошуком зворотних розріджених матриць .Нами запропоновано метод обчислень, побудований на використанні безпосередньо математичної моделі марківського ланцюга із дискретними станами та дискретним часом. Метод полягає у послідовному обчисленні імовірностей станів

.

Критерієм завершення процедури обчислень слугує:

, (11)

якщо відповідає поглинаючому стану.

Поняття є математичною абстракцією. Як доведено на практиці, для відповідних розрахунків достатньо обрати.

Позначимо середню кількість кроків до поглинання через . Тоді середній час виконання кроків до завершення програми (попадання у поглинаючий стан) можна обчислити як:

. (12)

Якщо уявити, що поглинаючий стан винесено за «кінець» алгоритму, то час його виконання в розрахунках має дорівнювати 0. Тоді з урахуванням (8) час визначається як:

. (13)

Якщо уявити, що ; то з урахуванням (9)

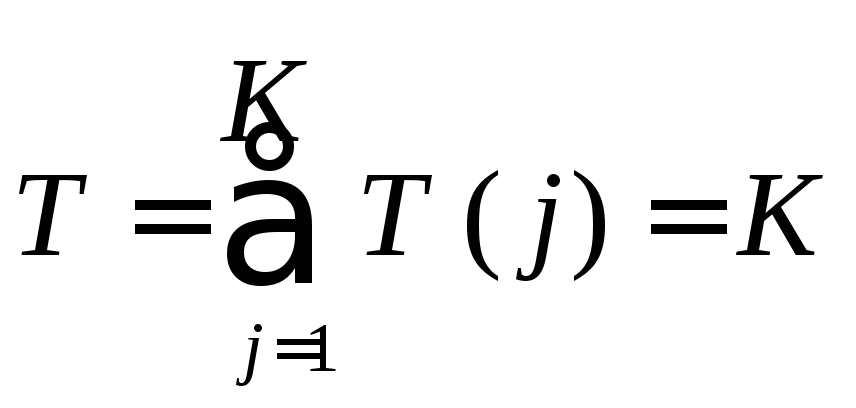. (14)

Визначимо загальний час перебування системи у стані .

На кожному кроці система знаходиться у стані середній час.

Тоді за кроків загальний час визначається як:

(15)

У середньому, кількість разів попадання системи у стан буде становити :

(16)

або

. (17)

Не важко бачити, що

(18)

За результатами досліджень була створена спеціальна програма обчислення означених характеристик. Наведемо приклад розрахунку параметрів , та програми, наведеної на рис. 1

Рис 3. Матриця перехідних імовірностей .

Результати розрахунків для випадку:

1. матриця перехідних імовірностей, як на рис. 3;

2. τ₁ =10, τ₂ =20, τ₃=50, τ₄=20, τ₅=10, τ₆=20.

Результати:= 665, = 34.5, = 1, = 10, = 1, = 9, = 4_,5, = 9.

Висновки. Згідно запропонованого методу, основною операцією обчислень є операція – добуток вектора на матрицюnxn, що достатньо просто реалізується для великихn, особливо зважаючи на те, що відповідні матриці сильно розріджені і для обчислень можна застосовувати спеціальні методи [5].