III. Решение системы линейных алгебраических уравнений

Когда говорят о решении системы линейных уравнений (СЛАУ), то имеют в виду, что дана система из N уравнений с N неизвестными, имеющая одно и только одно решение, которое и надо найти. В матричном виде это записывается, как Ax = b, где A - матрица размером nn, b и x - вектора с n компонентами. Вектор неизвестных умножается на матрицу коэффициентов и приравнивается к вектору правой части. Существует большое число методов решения задачи. Рассмотрим лишь некоторые из них.

3.1. Решение слау методом Гаусса

Метод Гаусса (обычный и модифицированный) - простейший метод, используемый на практике. Процедура решает неоднородную систему n линейных алгебраических уравнений с n неизвестными:

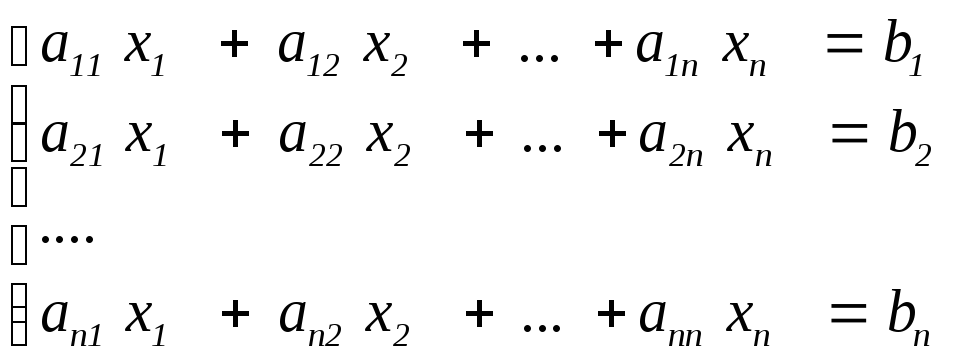. (3.1)

Записывают расширенную матрицу из коэффициентов и свободных членов:

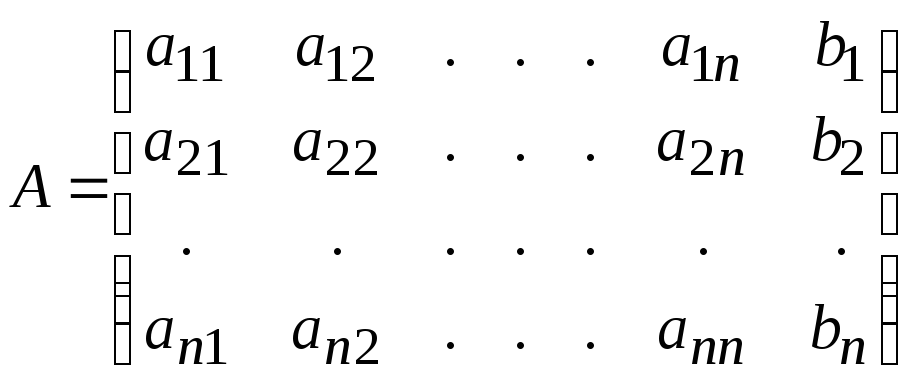. (3.2)

Вначале находят отличный от нуля коэффициент при x₁ . Соответствующую строку матрицы переставляют с первой (если это необходимо). Получают матрицу с диагональным элементом a₁₁  отличным от нуля. Разделив элементы этой строки на диагональный элемент a₁₁ , получают:

.

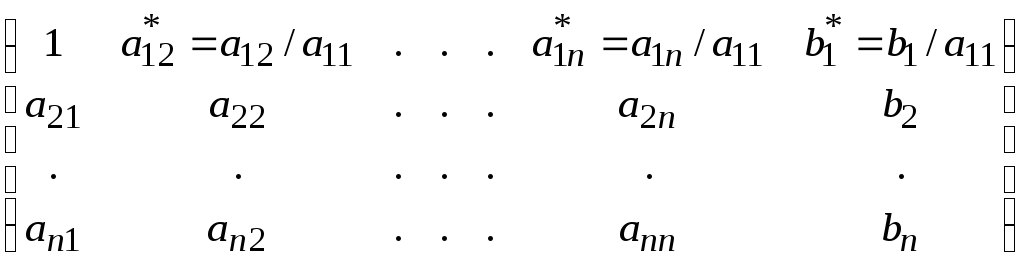При помощи этой строки исключают x₁  из исходной системы путем вычитания из последующих строк первой, умноженной на соответствующий элемент первого столбца:

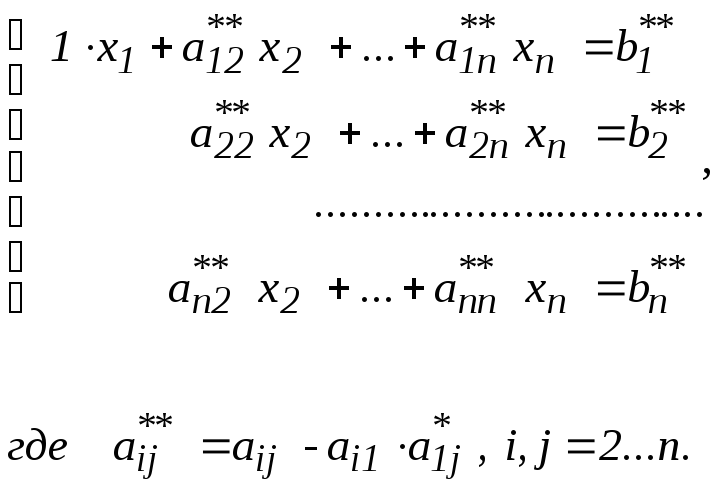
Описанную выше процедуру применяют к остальным уравнениям системы. Операции повторяют требуемое число раз, пока не приводят систему к треугольному виду:

Теперь легко определить x_n , x_n-1 , ..., x₁ .

3.2. Решение слау методом Гаусса-Жордана

Метод Гаусса-Жордана позволяет решать систему n линейных алгебраических уравнений с n неизвестными (3.1).

Записывают расширенную матрицу из коэффициентов и свободных членов, состоящую из n строк и n+1 столбцов (3.2).

Вначале добиваются, чтобы диагональный i-тый элемент был отличен от нуля. Для этого соответствующую i-тую строку меняют местами со следующими за ней до тех пор, пока не будет найден ненулевой i-тый диагональный элемент. Если такой элемент найти не удается, то система уравнений не имеет единственного решения. Таким образом, добиваются получения матрицы с диагональными элементами отличными от нуля.

Строки расширенной матрицы системы (то же, что и уравнения) можно менять местами, корни при этом не меняются. Решение системы не изменится, если умножить правую и левую части каждого уравнения на любое число, отличное от нуля.

Деля элементы i-той строки на диагональный элемент a_ii , добиваются, чтобы i-тый диагональный элемент стал равен единице:

, где i = 1..n; j = 1..n+1.

Например, в случае, если i = 1, матрица примет вид:

.

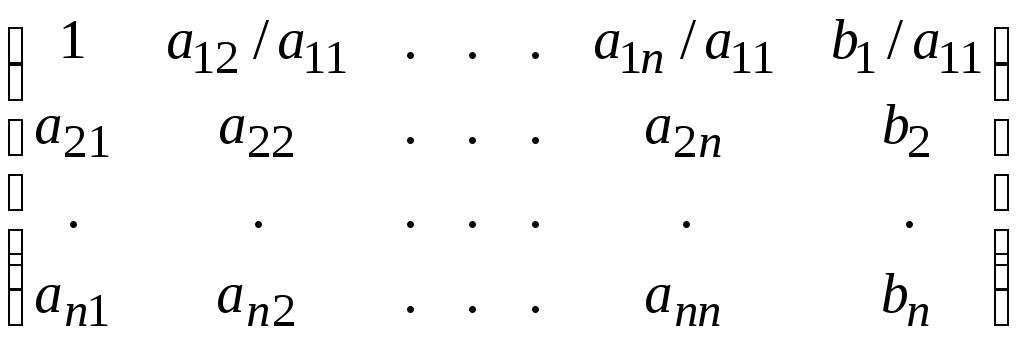Поскольку уравнения системы можно умножать на любые числа, а также складывать и вычитать, то элементы расширенной матрицы, стоящие в i-том столбце, кроме диагонального, можно обратить в 0. Для этого умножают i-тую строку на a_ki, где k  i, и произведение вычитают из k-той строки: . Например, еслиi = 1, а k = 2 матрица примет вид:

.

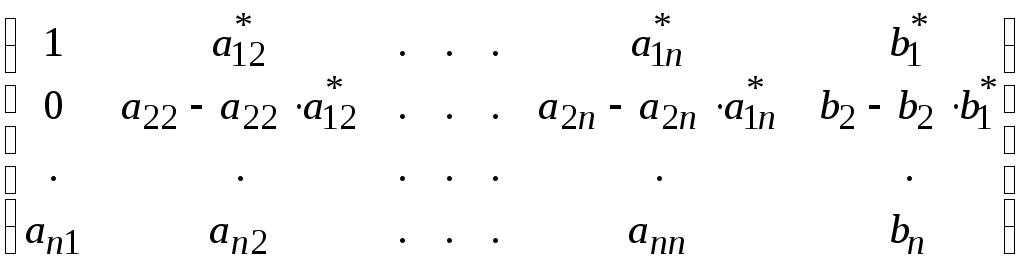Аналогично поступают со всеми элементами первого столбца, кроме диагонального. Следующий шаг решения состоит в обнулении всех элементов столбцов, исключая диагональные, что приводит к следующему результату:

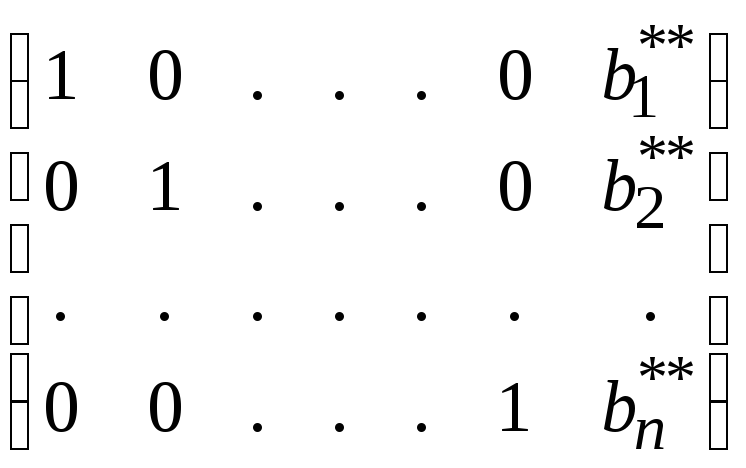
Таким образом, система принимает вид:

,

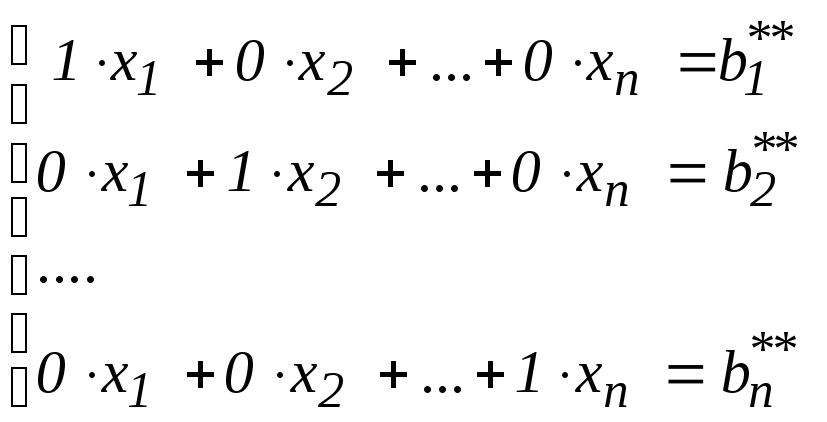откуда нетрудно найти искомое решение.

Метод Гаусса-Жордана можно использовать для нахождения обратной матрицы. Для поиска значений элементов матрицы, обратной заданной

А(NN):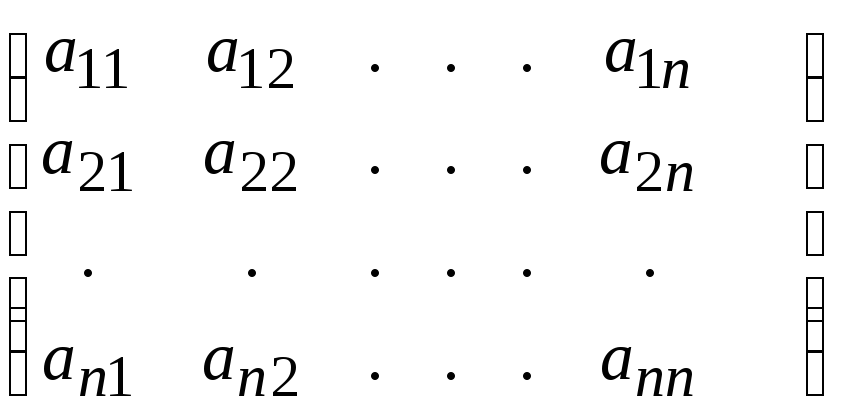этим методом, необходимо составить

расширенную матрицу размером n2n, дополнив исходную единичной n-мерной матрицей:

.

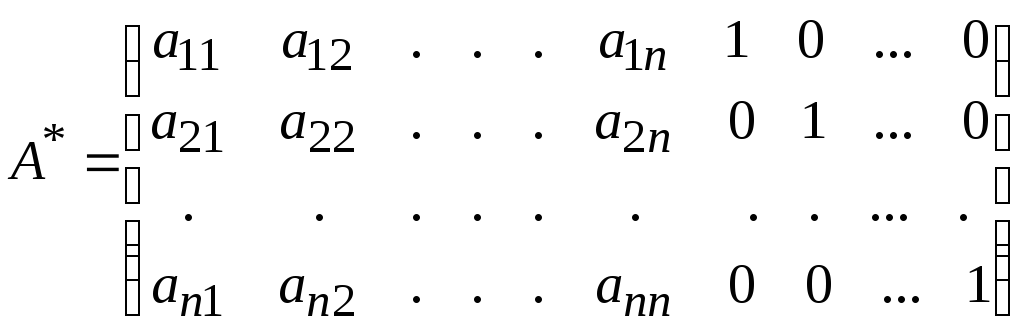Над полученной расширенной матрицей совершают преобразования, описанные выше для случая решения системы линейных уравнений методом Гаусса-Жордана. В результате преобразований получают матрицу вида:

.

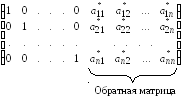Полученная после преобразований по методу Гаусса-Жордана матрица будет содержать значения элементов матрицы обратной матрице А(nn) на месте дописанной ранее единичной матрицы.

Например. Закон сохранения материи в химических реакциях сводится к решению системы линейных уравнений. Для корректного составления системы линейных уравнений, описывающих химическую реакцию, необходимо выразит ее в виде матричного произведения: .

В прямоугольной матрице [A] каждая строка описывает атом, а каждый столбец – молекулу (см. таблицу 3.1). В векторе-столбце [S] число элементов равняется столбцов в матрице [A] и каждый элемент представляет собой «неизвестный» стехиометрический коэффициент соответствующей молекулы в суммарном преобразовании. Условно считают, что эти элементы положительны для продуктов и отрицательны для реагирующих веществ. Матрицу [A] называют стехиометрической.

Например, если в реакционной смеси показано присутствие HI, HCl, Cl₂, I₂, то возможные элементарные реакции между ними могут быть представлены матрицей описанной в таблице 3.1, а вектор-столбец будет иметь вид:

.

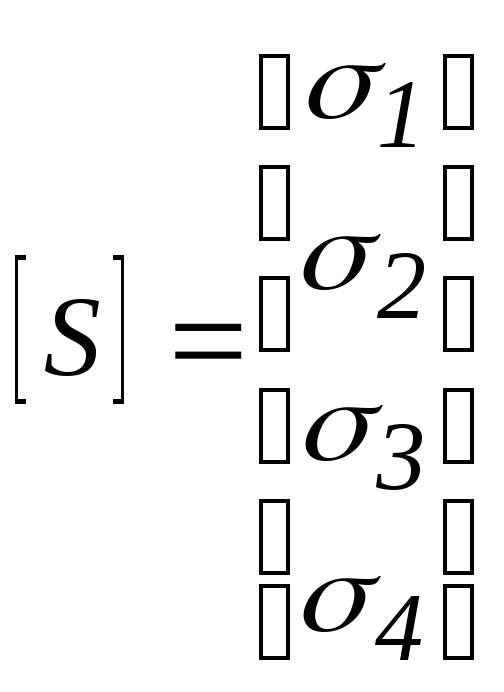Таблица 3.1

Построение стехиометрической матрицы для реакционной смеси, содержащей HI, HCl, Cl₂, I₂.

Номер строки	Атом	Число соответствующих атомов в молекулах
		HI	Cl2	HCl	I2
1	H	1	0	1	0
2	Cl	0	2	1	0
3	I	1	0	0	2

Здесь  - стехиометрические коэффициенты, которые необходимо найти (₁ - для HI; ₂ - для HCl; ₃ - Cl₂,. ₄ –для I₂. Для определения [S] перемножим матрицы [S] и [A] и приравняем элементы полученного вектора столбца нулю:

.

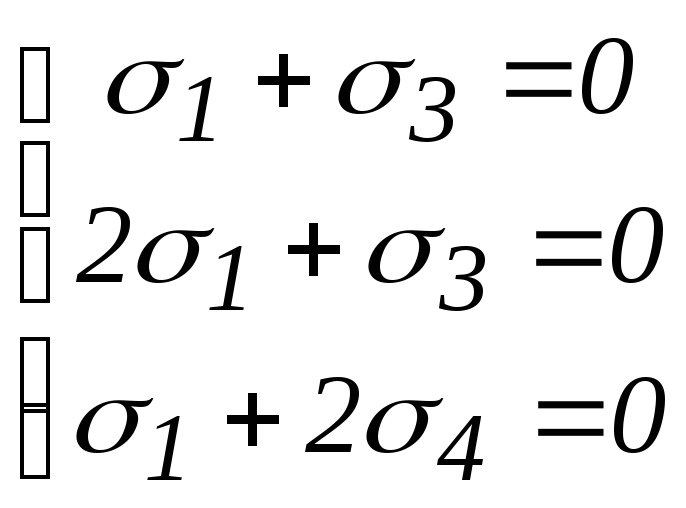В системе из трех уравнений с четырьмя неизвестными для решения одна переменная должна быть выбрана произвольно. Принимая ₄ = 1, получим ₁ = -2; ₂ = -1; ₃ = 3. Тогда конечная реакции имеет вид

2HI + Cl₂,= 2HCl + I₂.