IV. Приближение нелинейной функции

ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ

Пусть функция y = F(x) задана таблицей своих значений: , i = 0,1, ‑ n. Требуется найти многочлен фиксированной степени m, для которого минимально среднеквадратичное отклонение (СКО):

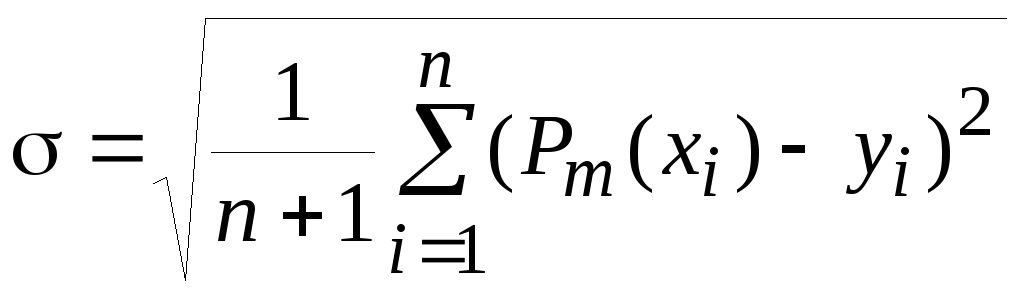. (4.1)

Так как многочлен определяется своими коэффициентами, то фактически нужно подобрать набор коэффициентов , отвечающий минимуму функции

.

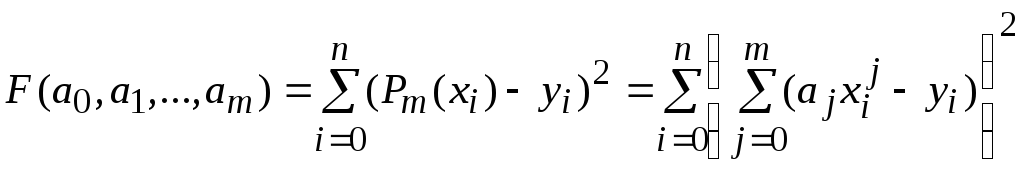Используя необходимое условие экстремума, ,k = 0,1,‑m формируют так называемую нормальную систему метода наименьших квадратов:

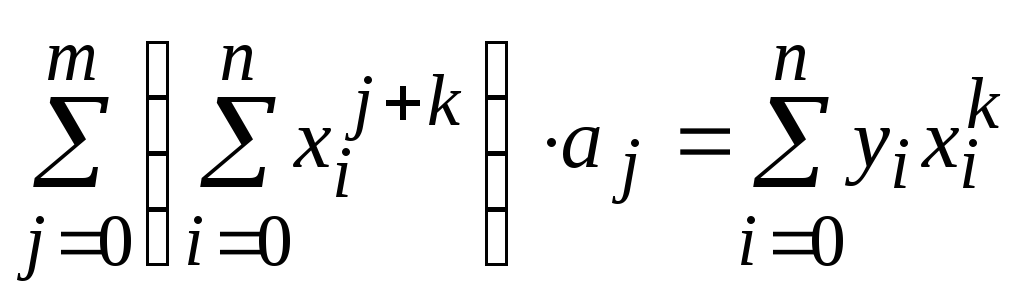, k = 0,1‑m.

Полученная система есть система алгебраических уравнений относительно неизвестных .

Например, для m = 2, , нормальная система уравнений имеет вид:

.

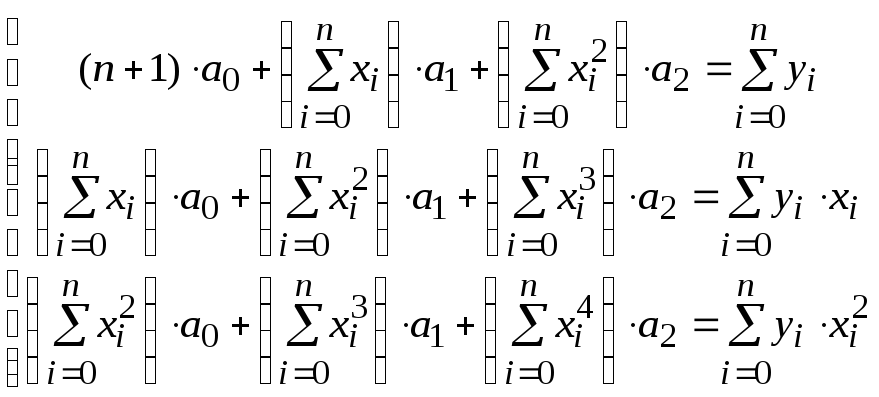Решая нормальную систему метода наименьших квадратов относительно коэффициентов полинома, находят полином степени m, удовлетворяющий условию минимума СКО.

Можно доказать, что определитель нормальной системы метода наименьших квадратов отличен от нуля, то есть решение существует и единственно. Решение нормальной системы можно найти, например, методом Гаусса, Крамера и др. Однако при высоких степенях m система является плохо обусловленной, поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5.

4.1. Приближение линейной функции

по методу наименьших квадратов.

П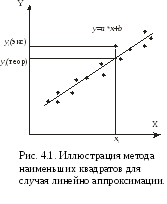ри обработке экспериментальных данных для расчета параметров, например таких, как энергия активации, энтальпия, порядок реакции, часто используют линейные соотношения между измеряемыми величинами или их функциями, если соотношение между экспериментально получаемыми величинами нелинейно. Например, между логарифмом константы скорости или логарифмом константы равновесия и обратной температурой.

При этом откладывают, попарно значения измеренных величин или их функций и проводят через них полином первой степени (далее прямую) (рис.4.1). По отрезкам, отсекаемым этой прямой на осях координат и тангенсу угла наклона прямой, рассчитывают значения необходимых физико-химических параметров.

Для того чтобы провести прямую через множество точек наилучшим образом, необходимо, что бы она удовлетворяла условию минимума среднеквадратичного отклонения (4.1).

Пусть даны n пар экспериментальных значений (x_i,y_i), которые должны быть связаны линейной зависимостью:

y=a + bx.

Сумму квадратов разностей экспериментальных значений y и соответствующих ординат на аппроксимирующей прямой можно записать следующим образом:

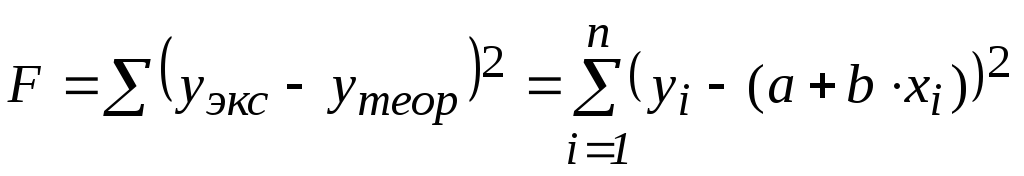
Надо подобрать такие значения параметров a и b, чтобы сума квадратов отклонений F была минимальна. Для этого надо приравнять нулю частные производные от F по a и b:

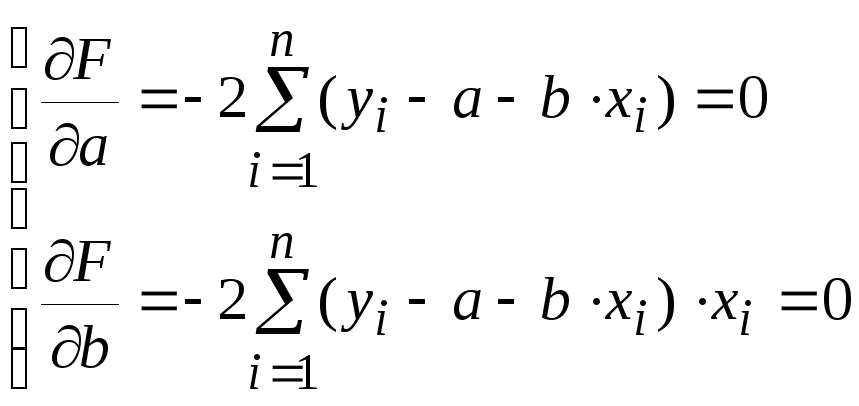
Деление обоих уравнений на (-2), раскрытие скобок и приведение подобных при параметрах и b дает следующую систему двух линейных уравнений с двумя неизвестными вид системы – коэффициентами прямой:

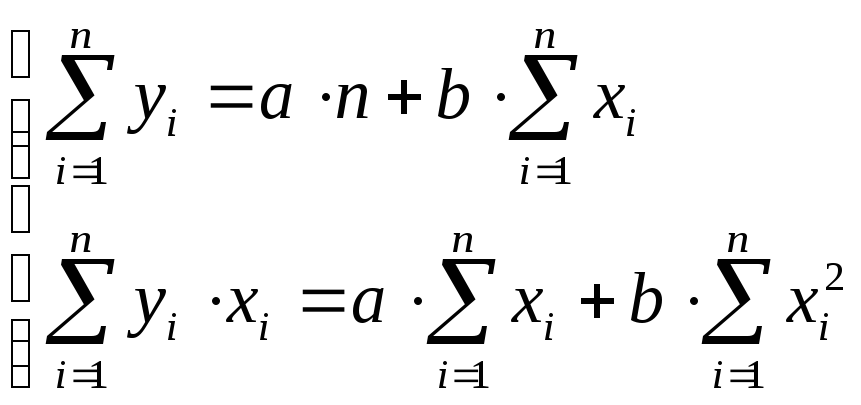. (4.2)

Суммы в системе (4.2) находят по экспериментальным значениям. Система решается относительно коэффициентов a и b любым известным способом. Полученные коэффициенты соответствуют прямой, удовлетворяющей минимуму СКО (4.1).

Наиболее важным показателем степени линейности связи y = F(x) служит коэффициент корреляции:

.

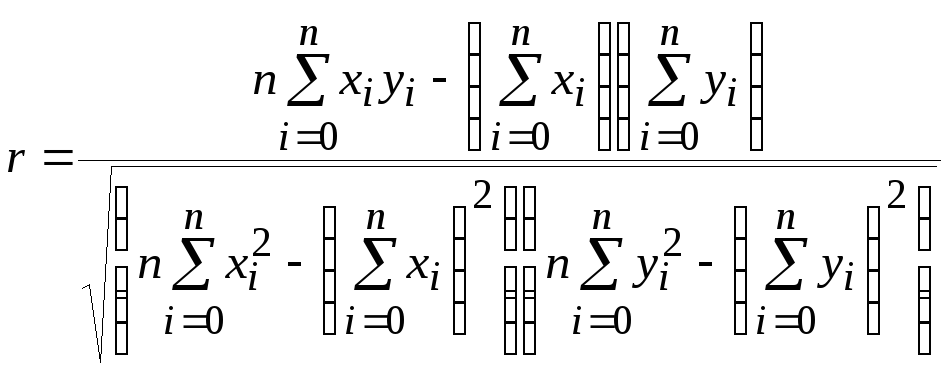Абсолютная величина r² всегда меньше единицы. Когда она равна единице, то x_i и y_i. связаны линейно и лежат на аппроксимируемой прямой. Когда r² = 0, между экспериментальными значениями линейной корреляционной связи не существует и следует искать нелинейную зависимость между ними.