49

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ЧИСЛЕННЫЕ МЕТОДЫ.

ПРИМЕНЕНИЕ В ХИМИИ

Методическое пособие по курсу

“Численные методы и программирование”

по специальности ХИМИЯ (011000)

ВОРОНЕЖ

2005

Утверждено научно-методическим советом химического факультета протокол № от .

Составители: доц. Протасова И.В.

асс. Крысанов В.А.

Науч.ред. ____________________

Методическое пособие подготовлено на кафедре физической химии химического факультета Воронежского государственного университета.

Рекомендуется для студентов химического факультета всех форм обучения.

Оглавление

I. ЧИСЛЕННЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
1.1. Интегрирование методом левых прямоугольников
1.2. Интегрирование методом правых прямоугольников
1.3. Интегрирование методом средних прямоугольников
1.4. Интегрирование методом Эйлера
1.5. Интегрирование методом Симпсона
1.6. Интегрирование методом Монте-Карло
II. ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
2.1. Метод последовательных приближений (Метод простых итераций)
2.2. Метод деления отрезка пополам (Метод дихотомии)
2.3. Метод Секущих
2.4. Метод касательных (Ньютона-Рафсона)
III. РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
3.1. Решение СЛАУ методом Гаусса
3.2. Решение СЛАУ методом Гаусса-Жордана
3.3. Решение СЛАУ методом Крамера
3.4. Итерационный метод решения системы линейных алгебраических уравнений (метод Гаусса-Зейделя)
3.5. Решение системы нелинейных уравнений
IV. ПРИБЛИЖЕНИЕ НЕЛИНЕЙНОЙ ФУНКЦИИ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
4.1. Приближение линейной функции по методу наименьших квадратов.
4.2. Линейная регрессия общего вида
4.3. Интерполяция полиномом Лагранжа
4.4. Интерполяция с помощью сплайн-функции
V. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
5.1. Метод Эйлера решения обыкновенного дифференциального уравнения первого порядка
5.2. Метод Рунге-Кутта четвертого порядка для решения уравнения первого порядка
5.3. Методы прогноза и коррекции
5.4. Решение систем дифференциальных уравнений

I. Численные методы интегрирования

При решении задач научного и инженерно-технического характера математическими методами часто возникает необходимость проинтегрировать какую-либо функцию. Есть функции, которые невозможно интегрировать аналитически, т.е. только в некоторых случаях по заданной функции можно найти первообразную. Общим способом интегрирования любых функций является численное интегрирование, методы которого в большинстве своем просты и легко переводятся на алгоритмические языки.

Из курса математического анализа известно, что выражение F(x) + C, где F(x) – первообразная функции F(x) и С – произвольная постоянная, называется неопределенным интегралом от функции f(x) и обозначается символом , причемF(x)называется подынтегральной функцией, F(x)dx – подынтегральным выражением, x – переменной интегрирования; –знак неопределенного интеграла. Таким образом, по определению , если.

Если существует предел 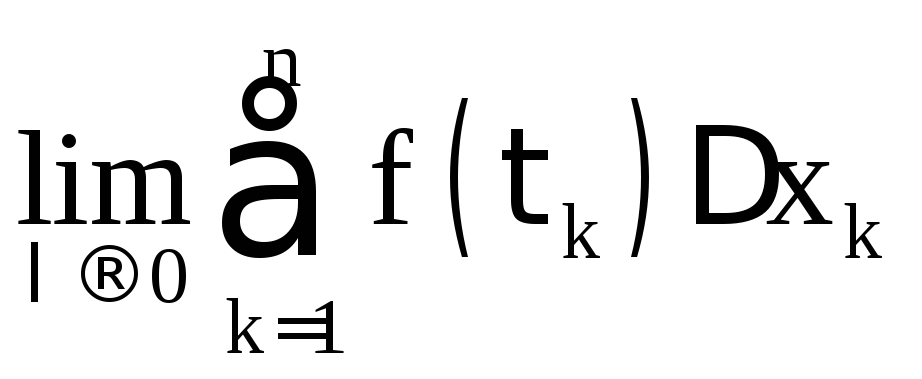, не зависящий от способа разбиения отрезка [А, Е] и выбора точек _k, то этот предел называется определенным интегралом функции f(x) на отрезке [A, E] и обозначается символом 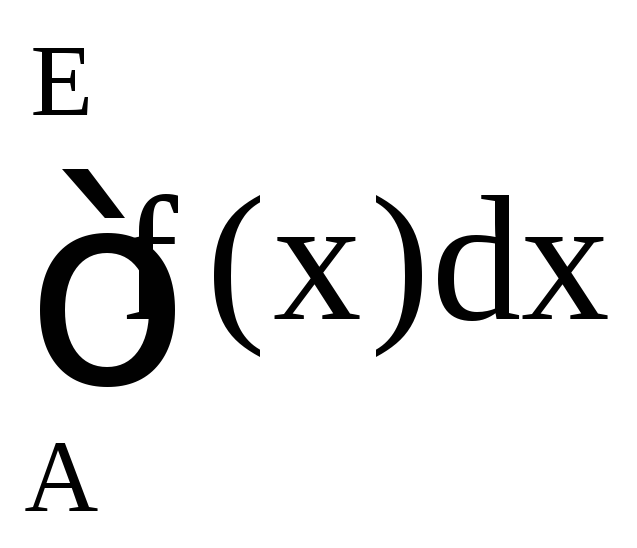, т.е..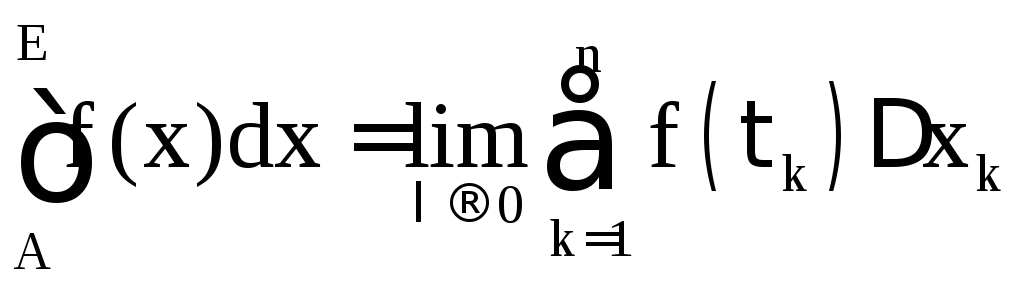

При этом 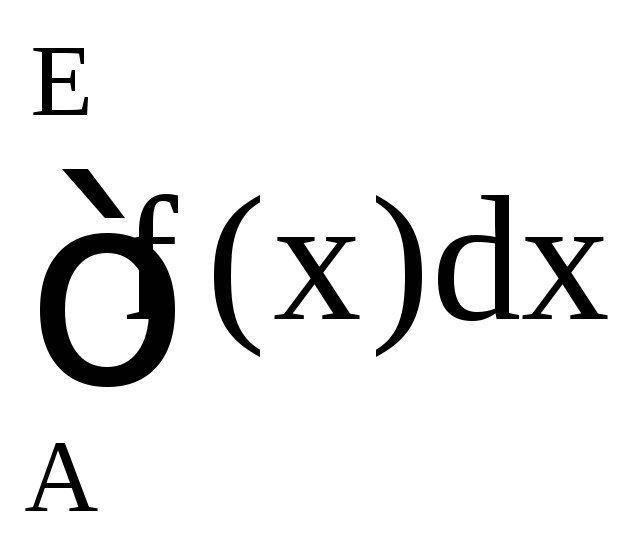называетсяинтегралом на отрезке [A, E], числа А и Е – пределами интегрирования (А – нижний предел, Е – верхний предел), а сумма 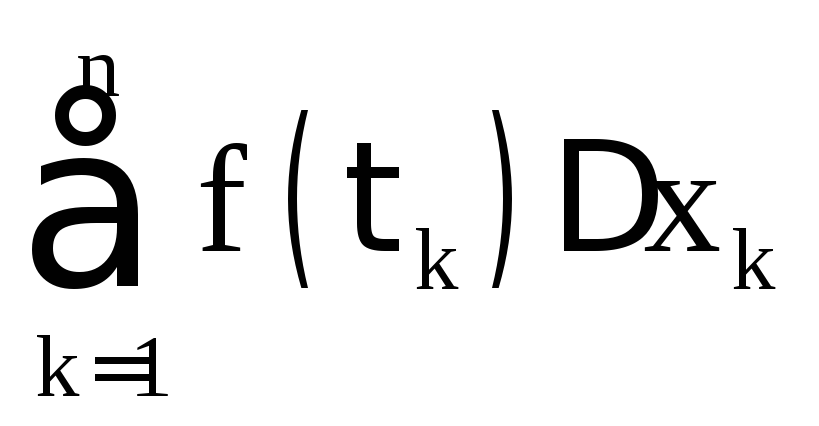–интегральной суммой.

Если функция F(x) непрерывна на отрезке [A, E], то определенный интеграл от этой функции в пределах от А до Е существует и его можно вычислить по формуле Ньютона-Лейбница:

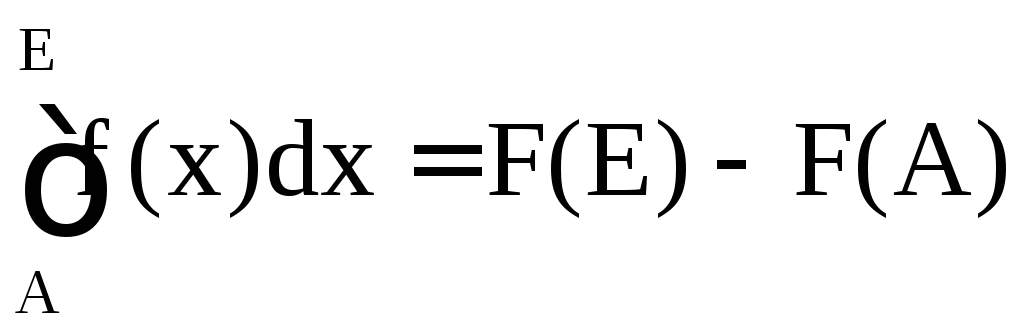. (1.1)

Здесь F(x)– первообразная функции F(x).

Для большинства функций первообразную F(x) не удается выразить через элементарные функции. Кроме того, при практических расчетах очень часто аналитическое выражение подынтегральной функции неизвестно, и она задана в виде таблицы значений в некоторых точках интервала наблюдения. Все это приводит к замене определенного интегрирования численными методами. Задача численного интегрирования состоит в следующем: требуется найти определенный интеграл на отрезке [A, E], если подынтегральная функция задана таблично.

Геометрически интеграл функцииF(x)в пределах от А до Е представляет собой площадь криволинейной трапеции, ограниченной графиком этой функции, осью х и прямыми x = A и x = E. Представленный ниже рис.1.1 иллюстрирует описанную картину.

Численные методы также позволяют избежать громоздких расчетов в тех случаях, когда результат приемлем с определенной степенью точности. Точность вычислений  (максимально допустимая ошибка в результате всех вычислений, из которых складывается погрешность), как правило, оговаривается заранее при постановке задачи. Точность вычислений будет достигнута, если абсолютная погрешность (абсолютное значение разности между точным и приближенным значениями) не превосходит (очень маленькое положительное число).

Сущность большинства численных методов вычисления определенных интегралов состоит в замене подынтегральной функции F(x)аппроксимирующей функцией (x), для которой легко можно отыскать первообразную среди элементарных функций:

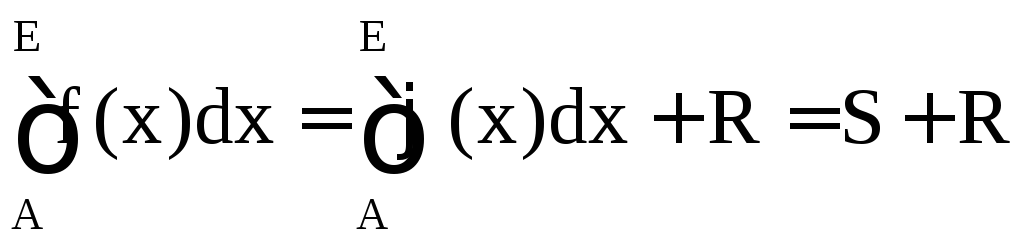. (1.2)

Здесь S – приближенное значение интеграла, а R – погрешность вычисления интеграла.

Для получения аппроксимирующей функции, когда подынтегральная функция задана таблично, прибегают к теории интерполяции. Задача нахождения интерполирующей функции становится однозначной, если в качестве интерполирующей для функции F(x), заданной n+1 своими значениями, выбрать многочлен степени не выше n L_n(x), значения которого в узлах интерполяции (точках разбиения отрезка интегрирования) совпадают со значениями подынтегральной функции (табличными значениями).

Используемые на практике методы численного интегрирования можно классифицировать в зависимости от способа аппроксимации подынтегральной функции:

• методы Ньютон - Котеса, основанные на полиномиальной аппроксимации подынтегральной функции;

• сплайновые методы, основанные на аппроксимации подынтегральной функции сплайнами, представляющими собой кусочные полиномы;

• методы наивысшей алгебраической точности, использующие неравноотстоящие узлы, вычисленные по алгоритму, обеспечивающему минимальную погрешность интегрирования;

• методы Монте-Карло, в которых узлы интерполяции выбираются при помощи датчика случайных чисел;

• специальные методы, алгоритмы которых разрабатываются на основе особенностей конкретных подынтегральных функций.

В настоящей работе будут рассмотрены шесть методов численного интегрирования: методы прямоугольников (левых, правых, средних), метод Эйлера (метод трапеций), метод Симпсона (метод парабол) и метод Монте-Карло.