II. Численное решение нелинейных уравнений

Нахождение корней уравнения - это одна из древнейших математических проблем, которая не потеряла своей остроты и в наши дни: она часто встречается в самых разнообразных отраслях науки и техники, в том числе и в химических науках и технологиях.

В общем случае, если имеется некоторая функция F(x), то бывает необходимо найти такие значения аргумента x, для которых

F(x)=0. (2.1)

Функция F(x) может быть алгебраической или трансцендентной. Будем предполагать, что она дифференцируема.

Функции, рассматриваемые далее, не имеют аналитических формул для своих корней в противоположность, например, квадратному уравнению. Поэтому приходится пользоваться приближенными методами нахождения корней, которые в основном состоят из двух этапов:

1. Отыскание приближенного значения корня.

2. Уточнения приближенного значения до некоторой степени точности.

Очень часто приближенное значение корня бывает известно из физико-химических соображений, в других случаях можно использовать графические методы оценки приближенного значения корня. Кроме того, существуют специальные методы нахождения приближенного корня для того практически важного случая, когда F(x) является полиномом.

Рассмотрим различные методы, относящиеся ко второму этапу нахождения корней уравнения - уточнению первоначального приближения. Численный метод, в котором производится последовательное, шаг за шагом, уточнение первоначального грубого приближения, называется методом итераций. Каждый шаг в таком методе называется итерацией. Если при последовательных итерациях получаются значения, которые все ближе и ближе приближаются к истинному значению корня, то говорят, что метод итераций сходится. В этом разделе будут рассмотрены несколько различных методов итераций для решения уравнений и рассмотрены условия их сходимости.

Следует подчеркнуть, что рассматриваемые методы относятся только к таким функциям F(x), которые непрерывны и дифференцируемы на отрезке нахождения корня.

2.1. Метод последовательных приближений (Метод простых итераций)

Предположим, что уравнение (1.1) переписано в виде

(2.2)

Это преобразование можно сделать различными путями. Например, если

(2.3)

где с0, то можно прибавить к правой и к левой частям x

(2.4)

Наконец, можно преобразовать уравнение к следующему виду:

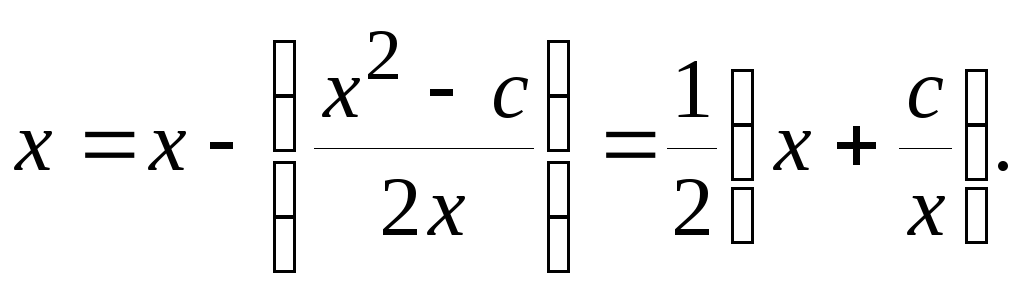(2.5)

Очевидно, что значения x, являющиеся корнями этого уравнения, равны .

Пусть x₀ - исходное приближение уравнения (2.2). Тогда в качестве следующего приближения примем

.

В качестве следующего приближения возьмем

.

Продолжая этот процесс дальше, в качестве n-го приближения необходимо положить

(2.6)

Геометрическое представление процесса нахождения коня уравнения (2.2) методом последовательных приближений показано на рис. 2.1 (a,b). Согласно рисунку в процессе решения находят точку пересечения кривых и.

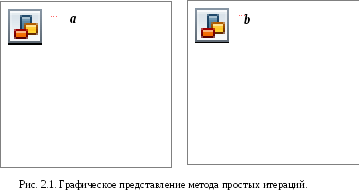
Процесс нахождения корня сводится к следующим этапам:

1. Выбирается некоторое x₀, являющееся начальным приближением (приближенным значением корня).

2. Вычисляется значение f(x₀) (рис.2.1).

3. Для нахождения значения x₁ устанавливают точку пересечения функции с прямой параллельной оси абсцисс и проходящей через точку f(x₀) (рис. 2.1). Абсцисса этой точки - и есть первое приближение корня уравнения (2.2).

4. Значение 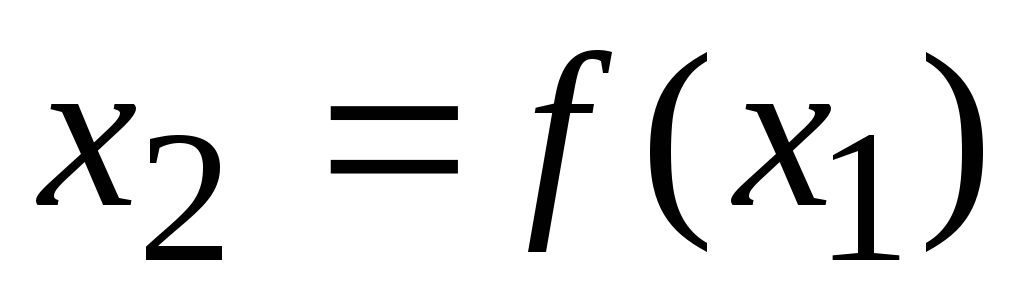находят, устанавливая точку пересечения функции с прямой параллельной оси абсцисс и проходящей через точкуf(x₁).

5. Процесс повторяется в том же порядке и дальше. На рис. 2.1 последовательность операций показана стрелками. Из рисунка 2.1 видно, что последовательные значения x сходятся к точке пересечения x = a. Процесс останавливается при выполнении условия 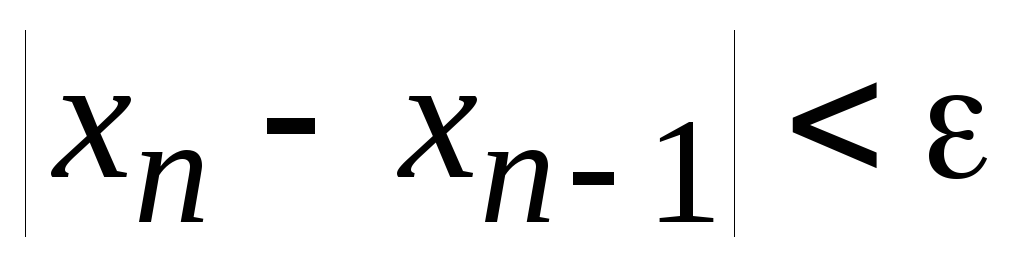, где - точность нахождения корня.

Достаточным условием сходимости метода последовательных приближений является накладываемое на значение производной функции ограничение

. (2.7)

Случай, когда производная функции положительна и меньше 1 иллюстрирует рис.2.1.a, а на рис.2.1.b показано нахождение корня методом последовательных приближений для функции, производная которой отрицательна и больше -1.

В случае методрасходится и значение корня найти невозможно. Следует обратить внимание, что неравенство (2.7) должно выполняться при всех значениях x_n, вычисляемых в ходе решения задачи. Если производная в некоторых точках x_i меньше, а в других точках x_j больше 1 по абсолютной величине, то процесс нахождения корня иногда будет сходиться, иногда расходиться, и в таком случае невозможно найти правильный корень.