1.1. Интегрирование методом левых прямоугольников

Пусть функцию, изображенную на рис.1.1, необходимо проинтегрировать численным методом на отрезке [A, E]. Разделим отрезок [A, E] на n равных между собой интервалов (рис.1.2, здесь n = 4). Проведем отрезки, соединяющие точки x₁, x₂ и x₃ c точками G, I и M соответственно. Это равносильно тому, что мы найдем значение функции f(x) в точках x₁, x₂ и x₃. Проведем прямые линии, параллельные оси x, из точек С, G, I и M слева направо до пересечения с перпендикулярными им линиями x₁G, x₂I, x₃M и EO. Сумму прямоугольников ACDx₁, x₁GJx₂, x₂Inx₃ и x₃MPE можно считать приближенным значением интеграла функции F(x) в пределах от A до Е. Площадь этих прямоугольников, а также сумму их площадей, найти очень легко. Достаточно ширину каждого прямоугольника, которая является постоянной величиной и равной , умножить на высоту (длину) прямоугольника, равную значению функцииF(x) в данной точке. Тогда приближенное значение интеграла функции F(x) равно

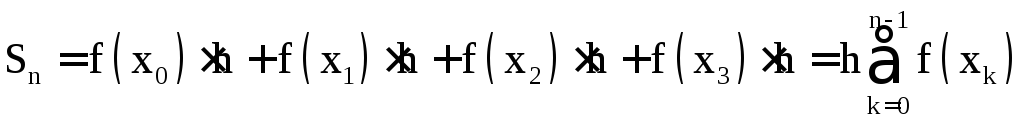. (1.3)

Данный метод численного интегрирования часто называют методом левых прямоугольников. Логично предположить, что раз есть метод левых прямоугольников, то должен быть и метод правых прямоугольников.

1.2. Интегрирование методом правых прямоугольников

Действительно, если мы проведем прямые линии, параллельные оси x, из точек G, I, M и О не слева направо, а справа налево до пересечения с перпендикулярными им линиями АС, x₁G, x₂I, и x₃M, и достроим получившиеся фигуры до прямоугольников, (удлинив отрезки АС, x₁G, x₂I, и x₃M до AF, x₁H, x₂K, и x₃L соответственно) то получим новое приближенное значение интеграла функции F(x) в пределах от A до Е (рис.1.3). Это значение рассчитывается следующим образом:

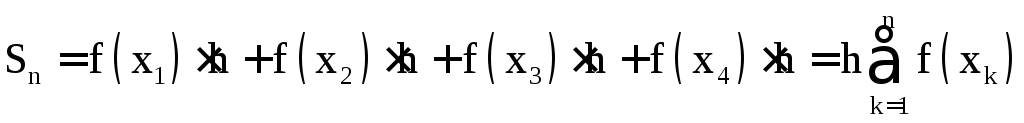. (1.4)

Очевидно, что расчеты значения интеграла для одной и той же функции F(x), проводимые по уравнениям (3) и (4) дадут разные результаты. Так, для реализуемого на рис.1.1-1.3 вида функции F(x), в задаваемых пределах интегрирования [A, E], приближенное значение интеграла, найденное методом левых прямоугольников всегда будет меньше истинного, независимо от количества разбиений n. Для метода правых прямоугольников, наоборот, приближенное значение интеграла всегда будет больше истинного. Поэтому чаще для численного нахождения значения интеграла пользуются методом средних прямоугольников или методом трапеций.

1.3. Интегрирование методом средних прямоугольников

При численном интегрировании функции f(x) методом средних прямоугольников высота прямоугольника находится как половина суммы значений функции f(x) в точках A и x₁, x₁ и x₂, x₂ и x₃, x₃ и Е. На рис.1.4 пунктирными линиями обозначены искомые высоты прямоугольников. Ширина прямоугольников остается неизменной и равной, как и в предыдущих методах, h.

Таким образом, для нахождения площади прямоугольника FFDx₁ необходимо вычислить значения функции в точках A и x₁ (f(А) и f(x₁)), затем сложить их и поделить пополам. Полученное число является значением функции F(x) в точке G и является высотой прямоугольника. Умножением высоты на ширину h получаем площадь рассматриваемого прямоугольника. Просуммировав площади всех прямоугольников, найдем приближенное значение интеграла функции F(x). В итоге получаем следующую формулу:

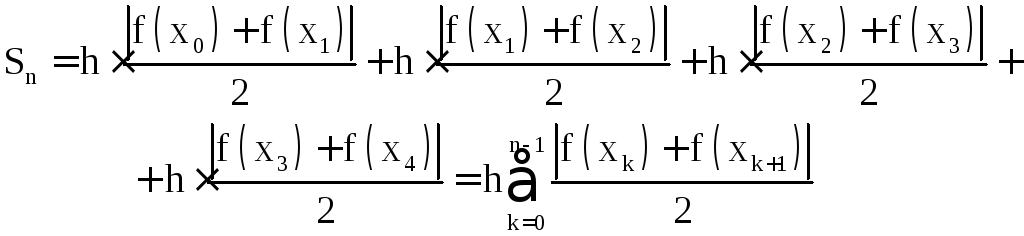. (1.5)

Как видно из рис.1.4, приближенное значение интеграла функцииf(x), найденное методом средних прямоугольников, будет точнее соответствовать истинному значению интеграла.