5.1. Метод Эйлера решения обыкновенного

дифференциального уравнения первого порядка

Пусть дано дифференциальное уравнение и начальное условие. Надо найти такую функцию, которая удовлетворяла бы как дифференциальному уравнению, так и начальному условию.

Выбирают число x настолько малым, чтобы для всех x в интервале (x₀,x₁), где , значения функции мало отличались от y₀ (функция непрерывна). Тогда для указанного интервала изменения x можно производную в левой части дифференциального уравнения заменить на близкое ей по величине отношение конечных приращений зависимой и независимой переменной: .

Из полученного соотношения выражают формулу, по которой находят y:

,

где есть значение производнойy в точке . Иными словами, на этом участке кривая заменяется отрезком прямой (касательной к ней в начале участка).

Таким образом, при заданных значениях x₀ и y₀ можно вычислить искомое значение функции, двигаясь с малым шагом по x вплоть до заданного значения:

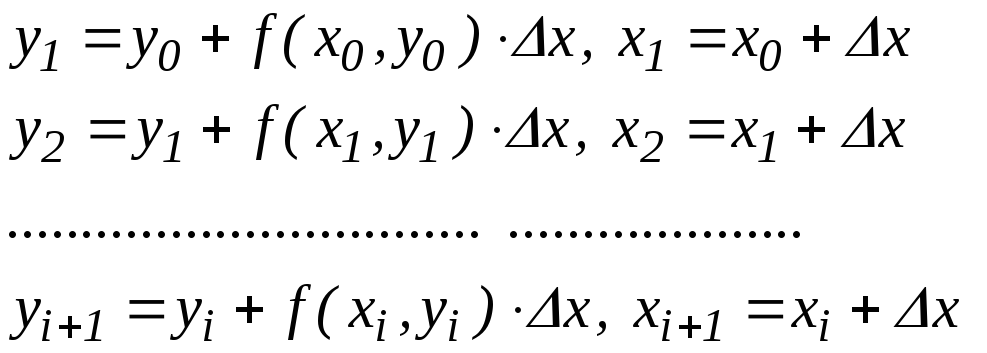. (5.5)

Геометрический смысл метода Эйлера представлен на рис.5.1. Ошибка определенияy прямо пропорциональна длине шага и будет тем меньше, чем меньше выбрана длина шага x.

Из уравнения (5.3) можно записать:

.(5.6)

Если в интеграле (5.6) функцию принять постоянной и равной значению в точкеx_i, то величина интеграл будет равна , так что формула (5.6) обращается в формулу (5.5).

Метод Эйлера не всегда дает практически требуемой точности вычислений, однако некоторая модификация алгоритма вычислений повышает точность искомых результатов. Рассмотрим вновь дифференциальное уравнение (5.3) с начальным условием (5.4). Если опять принять функцию постоянной и равной, но равной значению функции не в начале, а в середине участка.

Учитывая, что теперь x₁ является серединой отрезка (x₀,x₂), можно найти значение y₂ по формуле:

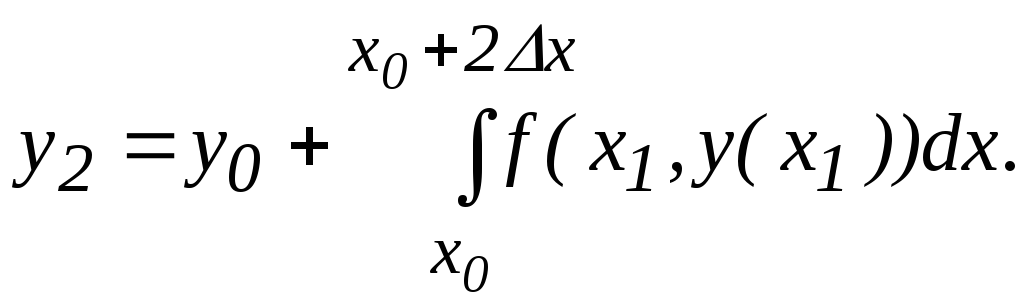
Так как , то. По найденному значениюнаходят, после чего можно найти, рассматривая участок (x₁,x₃) и т.д.

Таким образом, получают формулу улучшенного метода Эйлера для i  1:

(5.7).

По этой формуле нельзя, однако, отыскать y₁. Для его нахождения используют соотношение (5.5).

5.2. Метод Рунге-Кутта четвертого порядка

для решения уравнения первого порядка

Методы Рунге-Кутта обладают следующими отличительными признаками: 1) одноступенчатые; 2) согласуются с радом Тейлора до членов порядка h^P, где P – степень, различная для различных методов и называется порядком метода, а h = x – расстояние между точками; 3) не требуют вычисления производных, а требуют только вычисления значений самой функции. Следует отметить, что рассмотренный ранее метод Эйлера является одним из методов Рунге-Кутта первого порядка, так как он согласуется с разложением в ряд Тейлора вплоть до членов порядка h.

Одним из наиболее часто используемых методов интегрирования дифференциальных уравнений является метод Рунге-Кутта четвертого порядка. Из-за своего широкого применения его просто называют методом Рунге-Кутта. Для случая решения дифференциального уравнения первого порядка (5.3) этот метод сводится к следующим соотношениям:

,

где

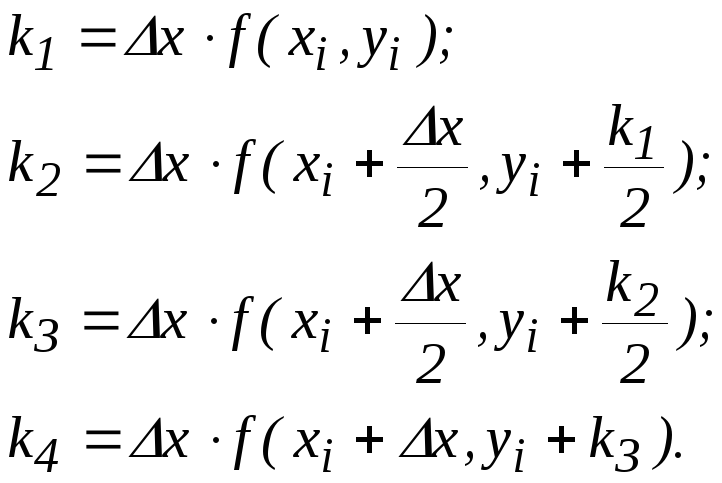
Решение уравнения методом Рунге-Кутта приводит к уменьшению ошибки вычисления значения функции в точке x. Ошибка метода прямо пропорциональна четвертой степени шага по x: