
Metody_optimizatsii
.pdf3
М И Н И СТ Е РСТ В О О БРА ЗО В А Н И Я РО ССИ Й СК О Й Ф Е Д Е РА Ц И И В О РО Н Е Ж СК И Й ГО СУ Д А РСТ В Е Н Н Ы Й У Н И В Е РСИ Т Е Т
Т .В. А за р но в а , И .Л . К а ш ир ина , Г .Д . Ч ер ны ш о в а
М Е ТОД Ы ОП ТИМ ИЗ А Ц ИИ
У чебноепособи е
ВО РО Н Е Ж
2003
4
У тверждено научно-методи чески м советом факультетаПМ М В ГУ .
Рец ензент: зав. кафи сследовани я операц и й Ростовского госуни верси тета, д.т.н., профЖ акС.В .
А з арнова Т . В . , К аш и ри на И . Л . , Ч ерны ш ова Г . Д . М етоды опти ми зац и и : У чеб. пособи е. – В оронеж: И зд-во В ГУ , 2003.- 86 с.
В |
пособи и |
рассматри вается |
ш и роки й |
круг |
задач |
математи ческого |
|
программи ровани я. |
И зложены анали ти чески е и |
чи сленны е методы |
реш ени я задач |
||||
безусловной и |
условной опти ми зац и и . |
При менени е каждого метода и ллю стри руется |
|||||
реш ени ями ти повы х при меров. При ведены задачи для самостоятельного реш ени я. |
|||||||
Пособи еподготовлено накафедрематемати чески х методови сследовани я операц и й |
|||||||
факультетаПМ М |
В оронежского государственного уни верси тета. Рекомендуется для |
||||||
студентов3 курсад/о и 5 курсав/о, обучаю щ и хся по спец и альности “ При кладная математи каи и нформати ка”.
5
§ |
1. |
П о ста но в ка |
за да чи ма тема тическо го |
|
|
||||||
|
|
пр о гр а ммир о в а ния |
|
|
|
||||||
Под задачей математи ческого программи ровани я пони мается задача |
|
||||||||||
нахождени я |
в векторном пространстве Rn |
такого вектора x *, |
которы й |
|
|||||||
обеспечи вает опти мальное |
(ми ни мальное |
и ли |
макси мальное) |
значени е |
|
||||||
функц и и |
f (x) и при этом при надлежи тнекоторой области Ω Rn . |
|
|
|
|||||||
Рассмотри м следую щ ую |
постановку задачи : |
|
|
|
|
||||||
|
|
|
|
→ min |
, |
) x(f |
|
|
(1) |
|
|
|
|
|
|
|
xΩ Rn |
|
|
|
|
|
|
где = |
1 |
n ) −( n -,мерны.., xx й xвектор, f (x) - функц и я, назы ваемая функц и ей |
|
||||||||
ц ели , |
Rn − допустиΩ моемножество. |
f (x) |
|
|
|
|
|||||
Задача пои ска макси мума функц и и |
своди тся к задаче пои ска |
|
|||||||||
ми ни мумапутем умножени я ц елевой функц и и на-1: |
|
|
|
||||||||
|
|
Ω |
n |
|
= − |
n |
− |
)) x( f ( min |
) x( f |
max |
|
|
|
|
|
Ω R |
x |
x R |
|
|
|
||
Задачапои сками ни мумаи макси муманазы вается задачей пои ска |
|
|
|||||||||
экстремума: |
|
|
( |
) → extr |
|
f x |
|
|
|
||
|
|
|
|
|
|
|
|
||||
xΩRn
Если Ω = R n , тои меетместо задачабезусловной опти ми зац и и . В проти вном
случае, т.е. если Ω Rn – задачаусловной опти ми зац и и .
О пред ел ение1. Т очка x*ÎW назы вается точкой глобального ми ни мума
функц и и |
f (x) намножествеΩ , если функц и я дости гаетвэтой точкесвоего |
||||
наи меньш его значени я, т.е. f (x*) £ f (x), |
"x ÎW . |
|
|||
При этом и спользуется обозначени е = |
).x(f min |
arg x* |
|||
|
|
|
|
xΩ |
|
О пред ел ение2. Т очка x*ÎW назы вается точкой локального ми ни мума |
|||||
функц и и |
f (x) намножествеΩ , если ε > 0, такое |
|
|||
что "x : (x ÎW) Ç (|| x − x* ||< ε ), справедли во неравенство f (x*) £ f (x) . |
|
||||
Замечани е1. В качественормы векторав R n и спользуется евкли дова |
|
||||
|
|
n |
|
|
|
норма: |
x ||= ||å xi2 |
|
|
||
|
|
i=1 |
|
|
|
О пред ел ение3. М ножество W Í Rn |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
назы вается вы пуклы м, если оно |
|
|
||||||||||||||||||||||||
содержи т отрезок, соеди няю щ и й лю бы едветочки и з множества Ω , т.е. |
|
|
||||||||||||||||||||||||
если x1 , x2 Ω и λ [0,1] справедли во: λ 1 ( |
λ)x2 |
|
|
Ω1. |
+ |
− |
|
|
||||||||||||||||||
О пред ел ение4. Ф ункц и я f (x), |
определенная навы пуклом множествеΩ |
|
|
|||||||||||||||||||||||
назы вается вы пуклой , если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− λ + x2f), |
λ≤(λ1 )+ |
1−x(1λf ) ( x |
|||||||||
1 2 Ω λ 1]0.,, [ |
, x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Замечани е1. В дальнейш ем будем назы ватьтакую функц и ю |
вы пуклой |
|
|
|||||||||||||||||||||||
вни з. Д ля вы пуклой вверх функц и и справедли во обратное неравенство: |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
1 2 |
1 1 λ 12]0Ω., [ |
|
, x λ,x −),x f+ λ( |
||||||||||||
О пред ел ение5. Задача(1 ) назы вается задачей вы пуклого программи ровани я |
|
|||||||||||||||||||||||||
(ЗВ П) , если |
f (x) -вы пуклая функц и я , аΩ - вы пуклоемножество. |
|
|
|
||||||||||||||||||||||
Д ля задачбезусловной опти ми зац и и необходи моеуслови еэкстремума |
|
|||||||||||||||||||||||||
сформули ровановтеоремеФ ерма. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Т ео р ема 1 (Ф |
ерма). Е сли |
х* - точкалокального безусловного экстремума |
|
|||||||||||||||||||||||
непреры вно ди фференц и руемой в т. х* |
функц и и f (x) , то всееечастны е |
|
||||||||||||||||||||||||
прои зводны епервого порядкавэтой точкеравны нулю . (В |
векторны х |
|
|
|||||||||||||||||||||||
обозначени ях,Ñf (x*) = 0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Замечани е2.Т очки , удовлетворяю щ и етеоремеФ ерма, |
|
назы ваю тся |
|
|
|
|||||||||||||||||||||
стац и онарны ми . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т ео р ема 2 (Дост ат очное условие экст ремума). |
Е сли встац и онарной |
|
|
|||||||||||||||||||||||
точке х* Î R n функц и я f (x) дважды ди фференц и руемаи матри ц аеевторы х |
|
|||||||||||||||||||||||||
частны х прои зводны х H(x*) (матри ц аГессе) положи тельно определена(т.е. |
|
|||||||||||||||||||||||||
всеееглавны еми норы Hk >0, k = |
|
) , |
то х* - точкалокального ми ни мума. |
|
||||||||||||||||||||||
1, n |
|
|||||||||||||||||||||||||
П р имер 1. Реш и тьзадачу |
|
|
|
|
|
|
|
|
|
|
x→ minx |
− |
|
+− x |
− |
2= x f+ x |
||||||||||
|
|
2 |
2 |
|
|
2 |
|
|
x |
|
x |
|||||||||||||||
|
|
1 |
|
2 |
|
|
3 |
|
|
|
|
3 1 2 |
|
|
|
3 |
|
|
|
|
|
|||||
Р ешение. Запи ш ем си стему: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ì df |
x1 |
= = 2,-0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
ï |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï df |
|
|
|
|
|
|
|
æ 1 |
|
2 |
|
4 |
ö |
|
|
|
|
|
|||||||
|
í |
|
|
|
x2 |
x == , 0- Þ x* = ç |
|
|
, |
|
|
, |
|
|
÷ |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
3 |
|
|
|
|
è 2 |
|
3 |
|
3 ø |
|
|
|
|
|
|||||||
|
ïdx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
ï df |
x3 |
|
|
|
x2 = 0 = 2- 2 - 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
îdx3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Провери м, вы полняю тся ли вполученной стац и онарной точкедостаточны е |
|
|||||||||||||||||||||||||
услови я экстремума. М |
атри ц авторы х частны х прои зводны х вданной задаче |
|
||||||||||||||||||||||||
|
|
æ |
|
02ö |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ç |
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
является постоянной: H = ç |
|
|
- 1÷0. В ы2 чи сли м главны еми норы : |
|
|
|||||||||||||||||||||
|
|
ç |
- 02 |
÷ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
è |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= > |
|
= |
× = |
> |
H 3 |
= |
H× 1 |
× |
+ |
|
|
|
=H2 > 0 Þ матри10 )1ц а 2 |
2( 2 |
, 0 |
4 2 |
|||||||||||||||
положи тельно определена, т.е. x * − точками ни мума. |
|
fmin |
= - |
19 |
. |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
Д ля задачсограни чени ями -равенствами |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
f0 |
x |
→ min, |
|
|
|
|
( |
) |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= i |
|
|
= |
|
|
|
, i (b)f x |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
, m1 |
|
|
|
|
|||||||||||||
необходи моеуслови еэкстремумаформули руется вви депри нц и паЛ агранжа. |
|
|
||||||||||||||||||||||||||||||
Т |
ео р ема |
|
3 (принципЛагранж а). Пусть х* - точкалокального экстремума |
|
|
|||||||||||||||||||||||||||
функц и и f0 (x) , при чем |
|
|
= |
|
|
0непреры( i),f x |
вно ди фференц и руемы |
в |
|
|
||||||||||||||||||||||
i |
|
|
, m |
|
|
|||||||||||||||||||||||||||
окрестности точки х* и векторы Ñ i |
|
|
|
= |
|
|
си мы . Т огда |
|
|
|||||||||||||||||||||||
|
|
|
, m1- ли(iнейнонезави*),f x |
|
|
|||||||||||||||||||||||||||
сущ ествуеттакой векторy* Î Rm , что для функц и и Л агранжа |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
− |
|
x))f (+Φ b y (= x )f (x y )( , |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å |
|
|
|
|
|
|
i |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
0 |
|
i i |
|
|
|
|
|||||
вы полняю тся следую щ и еравенства: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
*) =)10 *, Ñy( Fx |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
ì |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
í |
|
|
|
|
|
|
|
*) =)20 *, Ñy( Fx |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
î |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
При проверкедостаточны х услови й экстремумав некоторы х задачах |
|
|
|||||||||||||||||||||||||||||
условной опти ми зац и и можно пользоваться кри тери ем В ейерш трасса. |
|
|
||||||||||||||||||||||||||||||
Т |
ео р ема |
|
4 (крит ерийВейершт расса). |
Пусть f (x) |
- непреры вная функц и я, |
|
|
|||||||||||||||||||||||||
а множествоΩ представляетсобой компакт. Т огдасущ ествую тточки |
|
|
|
|||||||||||||||||||||||||||||
|
|
max |
min |
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
|||||
x |
, x |
|
|
|
|
= |
|
|
|
|
|
|
|
|
x),f ( |
|
min=(f |
x ) |
x) f. ( |
|
max (f |
|||||||||||
|
|
Ω , таки ечто |
|
|
|
|
|
ΩRn |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
ΩRn |
|
|
|
|||||
П р имер 2. Н айти условны й экстремум в задаче |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
( |
) = |
|
|
+ |
2 |
® extr |
|
|
x |
x f |
x |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 ( ) |
|
|
2 |
|
|
2 |
= 2 |
|
|
|
+ x |
|
x f x |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||
Р ешение. |
|
Ф ункц и и |
0 |
1 x) f( данной(x), |
задачи |
|
являю тся |
непреры вно |
|
|
||||||||||||||||||||||
ди фференц и руемы ми . |
О грани чени е здесь еди нственно, |
поэтому ли нейная |
|
|
||||||||||||||||||||||||||||
незави си мостьгради ентовограни чени й можетбы тьнаруш енали ш ьв случае, |
|
|
||||||||||||||||||||||||||||||
когда Ñ |
1 |
= 0,f |
(тx.е). |
|
|
|
= |
, |
) Þ( |
|
()= |
|
2 |
,= 0 . Oднакx оx точк0а0(0,0) xне2 2x |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
2 |
|
|
|
|||||
является |
|
допусти мой |
в |
данной |
задаче и , |
|
|
следовательно, |
не является |
|
|
|||||||||||||||||||||
реш ени ем. В оспользуемся при нц и пом Л агранжа. Ф ункц и я Л агранжаи меет |
|
|
||||||||||||||||||||||||||||||
ви д |
|
|
|
|
2 |
− x2 )− x |
|
|
2+Φy +( x= x x y )( , |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
1 |
2 |
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В ы пи ш ем необходи мы еуслови я экстремума
|
|
|
8 |
|
|
|
ì1) |
¶F x y)( , |
1 1 |
= 0, =x1 -y 2 |
|
|
|
ï |
¶x1 |
|
|
|
|
|
ï |
|
|
|
|
|
|
ï |
¶F x y)( , |
1 2 = 0, , =x1 -y 2 |
|
|
|
|
í |
¶x2 |
|
|
|
||
ï |
|
|
|
|
|
|
ï |
¶F x y)( , |
12 - 22 = 0 =x2 -x |
|
|
|
|
ï2) |
¶y1 |
|
|
|
||
î |
|
|
− |
(= 0. Равенствоx) x 2 y |
||
В ы чи тая и з первого уравнени я второе, получаем |
||||||
y1 = 0 |
|
|
|
|
1 1 |
2 |
невозможно, |
так как в проти вном случае |
первы е два уравнени я |
||||
си стемы несовместны . Значи т, x1 = x2 . И спользовавэто услови евпоследнем уравнени и , находи м подозри тельны енаэкстремум точки :
A: |
* |
= |
* |
yB:1, x x 1 |
|
|
* |
|
* |
|
1 |
2; 1=/, |
|
|
1 |
= , / 2 .-1= , y =1-x x 1 |
|||||
|
|
2 |
|
|
|
|
|
2 |
||
Д опусти моемножество в и сходной задачепредставляетсобой окружность, а, |
||||||||||
следовательно, компакт. |
К ак следует и з |
кри тери я |
В ейерш трасса, среди |
|||||||
подозри тельны х |
на экстремум точек данной |
задачи |
должны |
бы ть точка |
||||||
макси мума и точка ми ни мума. |
Т ак как |
0 |
− − |
< |
0 1)1,, |
тf(о fточк1() 1а, В |
||||
является точкой |
ми ни мума и f0min = -2 , а точка А - |
|
точкой макси мума и |
|||||||
f0max = 2 . |
|
|
|
|
|
|
|
|
|
|
П р имер 3. Н айти условны й экстремум в задаче
0 |
2 |
1 |
2 |
1 |
x2 ® minx x+4 = |
x3f+ x |
|||
2 |
|||||||||
1 |
|
2 |
|
|
|||||
1 ( ) |
1 |
2 = 4 + x |
x f x |
|
|||||
Р ешение. Ф ункц и и |
0 |
1 x) f(данной(x), |
задачи |
являю тся непреры вно |
|||||
ди фференц и руемы ми . О грани чени ездесьли нейное, |
Ñf1 x |
= )1,-1(ли( )нейно |
|||||||
незави си мая си стема. |
|
|
|
|
|
|
|
|
|
1. Запи ш ем функц и ю Л агранжа: |
|
|
|
|
|
|
|
||
2 |
|
|
1 |
2 |
|
1 |
1 |
2 |
2 |
2 |
1 |
2. В ы пи ш ем необходи мы еуслови я экстремума
ì1) |
¶F x y)( , |
|
|
|
|
xy |
= x, 0-= |
||
ï |
|
¶x1 |
|
|
|
|
1 1 |
2 |
|
ï |
|
|
|
|
|
|
|
||
ï |
|
¶F x y)( , |
4 |
|
|
yx1 = x,2=0- |
|||
í |
|
¶x2 |
|
|
|
||||
ï |
|
|
|
|
|
|
|
||
ï |
|
¶F x y)( , |
4 x |
x |
|
= 0 -= |
|||
ï2) |
|
|
|
2 |
|||||
|
|
|
|||||||
î |
|
¶y1 |
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|||
|
1 - x2 )- x |
+ y 4( +x |
||
6 + |
4 |
|
|
|
|
ìx* |
= , |
12 |
|
Þ+ |
ï |
1 |
|
|
íx2* = -8, |
|
|||
|
ï |
|
= 40 |
|
|
ïy* |
|
||
- |
î |
1 |
|
|
|
|
|
|
|
Д опусти моемножество в и сходной задачепредставляетсобой прямую , т.е. неявляется компактом.
3. Посчи таем вторы е частны е прои зводны е по х для функц и и Л агранжа :
2 Fd y)(x, |
2 Fd y)(x, |
2 Fd y)(x, |
|||||
|
= 6, |
|
= 1, |
|
|
|
= 4. |
dx2 |
dx2 |
|
dx |
|
|||
|
|
1 |
2 |
dx |
|||
1 |
|
2 |
|
|
|
||
( )
Fx+x =4x
9
4. Состави м второй ди фференц и ал |
|
|
|
2 |
|
|
|
|
|
2 |
8 |
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
6+ dx*). F( *,+dx |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
2 |
|
Проди фференц и ровавуравнени есвязи |
x1 + x2 = 4, получи м |
1 = −dx2 . |
|
dx |
|||||||||||||||||
Подстави м это вы ражени евди фференц и ал: |
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
2 |
2 |
2 |
-dx= |
2 |
. Т а+ккаdxFк- |
2 |
Fdxd=8y |
x<dx06, то*)*)точкd((y*,а*,x* |
|
|||||||||
|
|
|
2 |
2 |
2 |
2 |
|
|
|||||||||||||
является точкой макси мума. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При |
реш ени и |
больш и нства |
|
|
задач проверка |
услови я |
ли нейной |
||||||||||||||
незави си мости |
векторов Ñ i |
|
= |
|
|
точка х* |
|||||||||||||||
|
, m1 затруднена(i *),f x , так как |
||||||||||||||||||||
заранее неи звестна. |
О днако |
это |
|
требовани е |
является |
сущ ественны м. |
|||||||||||||||
Прои ллю стри руем это наследую щ ем при мере. |
|
|
|
|
|
|
|
|
|
||||||||||||
П р имер 4. Н айти условны й экстремум в задаче |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
0 |
= x1f →xmin |
|
|
( |
) |
|
|
|
|
|
||||||
|
|
|
|
|
1 ( ) |
|
3 |
2 |
= 0 +x= - x f x |
|
|
|
|||||||||
Р ешение. |
|
|
|
|
1 |
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. Запи ш ем функц и ю |
Л агранжа: |
|
|
|
3 |
|
2F) x+ y =( x x y )( , |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
- x |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
11 |
1 |
2 |
|
|
|
|
|
|
|
|
|
2. В ы пи ш ем необходи мы еуслови я экстремума |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
ì |
¶F x y)( , |
|
|
1 12 = 0, =x1 +y 3 |
|
|
|
|
|||||||||
|
|
|
|
ïa) |
|
|
|
|
|
|
|||||||||||
|
|
|
|
ï |
¶x1 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
ï |
¶F x y)( |
|
|
2 = 0, |
=x2-y |
|
|
|
|
|
|||||||
|
|
|
|
í |
|
¶x2 |
|
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
¶F x y)( |
, |
3 |
|
2 |
|
|
-x |
|
|
|
|
|
|
|||
|
|
|
|
ïb) |
¶y1 |
|
|
|
1 |
|
2 = x0 |
|
|
|
|
|
|
|
|||
|
|
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
И з второго равенстваследует, что ли бо y1 =0, ли бо x2 |
= 0 . |
|
|
|
|
||||||||||||||||
При y1 |
=0 первое равенство невозможно (1=0), |
значи т x2 = 0 . Н о и з |
|||||||||||||||||||
третьего |
равенства |
получаем |
x2 = 0 |
и |
первое равенство снова |
|
не |
||||||||||||||
вы полняется (1=0). |
В и тоге получаем, что си стема несовместна и точек, |
||||||||||||||||||||
подозри тельны х наэкстремум, нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
О днако, |
проанали зи ровав и сходную |
постановку задачи , нетрудно |
|||||||||||||||||||
убеди ться, что онаразреш и ма. И з ограни чени я следует, |
что x1 ³ 0 (таккак |
||||||||||||||||||||
x1 = (3 |
|
)2 ). |
Поэтому точка x*=(0,0) является реш ени ем данной задачи. |
||||||||||||||||||
x2 |
|||||||||||||||||||||
При нц и пЛ агранжа неработает, потому что вточке x* наруш ено требовани е
ли нейной незави си мости гради ентов: 1 |
|
* 2 |
* |
Ñ( x) 2- =, |
|
1 |
2 = ,0)0. |
||
Ч тобы и збежатьпроверки ли нейной незави си мости гради ентов в |
|
|||
рассмотрени евводи тся такназы ваемая расш и ренная функц и я Л агранжа: |
||||
~ |
m |
- x))f F(+ b y ( |
= x )f (y |
|
å |
||||
ii i 0 0 0
i=1
Тео р ема 5 (расширенныйпринципЛагранж а). Пусть х* - точкалокального
dx=
x) 3( f( (x
yx )y , ( ,
экстремума функц и и f0 (x) , при чем i |
= |
|
0непреры( i),f x вно |
, m |
ди фференц и руемы в окрестности ненулевой вектор( y0* ,y*) Î R m+1 , функц и и Л агранжа
~
вы полняю тся следую щ и еравенства:
10
|
точки х.Т огдасущ ествуеттакой |
|
|||||
= |
* |
y* |
) , чтy о ,дл...,я расш* ( и ренной |
|
|||
|
1 |
m |
|
|
|
|
|
|
|
m |
- |
|
x))f F(+ b y ( |
= x )f (y yx )y , |
|
|
|
å |
i |
||||
|
|
i=1 |
|
i i |
0 |
0 0 |
|
|
|
|
|
|
|
|
|
ì
ï
í
ï
î
*
x 0
*
y 0
*) = 0, )1 *,y Ñy( Fx *) = 0, )2 *,y Ñy( Fx
В результатеоты скани е подозри тельны х наэкстремум точекможет |
|
||||||
осущ ествляться по следую щ ему алгори тму: |
|
|
|
|
|
||
Ш аг1. |
Состави тьрасш и ренную |
функц и ю Л агранжа: |
|
|
|
|
|
|
~ |
m |
- |
|
x))f F(+ b y ( |
= x )f (y yx )y , ( , |
|
|
å |
i |
|||||
|
|
i=1 |
|
i i |
0 |
0 0 |
|
Ш аг2. |
|
|
|
|
|
|
|
Запи сатьнеобходи мы еуслови я экстремума |
|
|
|
|
|||
ì
ï
í
ï
î
0
x
0
y
) =),0 1, y( Ñy Fx ) )=,02 , y( Ñy Fx
Шаг3. Реш и тьси стему для двух случаев
1)y0=0;
2)y0=1
В результатенайти подозри тельны енаэкстремум точки x*.
В озврати мся кпр имер у4.
1. Состави м расш и ренную функц и ю Л агранжа.
|
|
|
3 - x 2F) x+ y ( x= y y x y) , ( , |
||||
|
|
|
1 0 |
1 |
2 |
1 |
0 |
2. В ы пи ш ем необходи мы еуслови я экстремума |
|
|
|
|
|||
ìa) |
¶F x y)( , |
0 |
2 |
= 0,= yx +y 3 |
|||
ï |
¶x1 |
1 |
1 |
|
|
|
|
ï |
|
|
|
|
|
|
|
ï |
¶F x y)( , |
|
= 0, |
=x2-y |
|
||
í |
1 |
2 |
|
||||
ï |
¶x2 |
|
|
|
|
|
|
ï |
¶F x y)( , 3 |
2 |
=x0 |
-x |
|
|
|
ïb) |
1 |
2 |
|
|
|||
î |
¶y1 |
|
|
|
|
|
|
3. Положи м y0=0. |
|
|
|
|
|
точку (0,0). |
|
Реш ая полученную си стему, находи м еди нственную |
|
||||||
При y0=1, какмы ужевы ясни ли , си стеманесовместна. |
|
||||||
За да чи для са мо сто ятельно го р еш ения
1.Д оказать, что всякая точкалокального ми ни мумав задачевы пуклого программи ровани я является точкой глобального ми ни мума.
2.Н айти точки безусловного экстремумафункц и й.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
1 |
2 1 |
|
2 → extr+ |
− − |
x + x 2 |
|
x |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|||||||||
|
2) |
4 |
4 |
|
|
|
|
|
|
|
2 |
® extr ++ |
|
-) |
x |
x(x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
2 |
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3. |
Н айти условны й экстремум в задачах: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
12 + |
22 ® extr |
|
x |
|
x |
12 - 22 ® extr |
x |
|
|
x 1 |
+ |
2 → extr |
|
x3 |
4x |
|
|
|
||||||||||||||
|
1) |
( 1 |
) |
2 |
|
|
2 |
|
|
|
|
|
2) |
2 |
+ |
2 |
=x1 |
x |
|
3) |
|
2 |
+ |
2 |
=x1 |
x |
|
|
|
|
|
|
||
|
|
|
|
|
2 |
-= 4 + x x |
11 |
2 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|||||||||||||||
4. Реш и тьзадачу спомощ ью |
расш и ренной функц и и Л агранжа |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
x |
® extr |
|
|
|
|
|
|
|
|
x 2 |
® extr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1) |
|
23 |
3 |
|
|
|
|
|
= 0 + |
|
2) |
1 |
2 |
|
2 |
|
|
|
=+0 |
|
x-x |
x2 |
2x |
|
|
|
|
|
|||||
|
|
|
1 |
2 |
|
|
1 |
2 |
x -x3x |
|
x |
|
2 |
1 |
2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
5. |
Д оказ ать, |
что ограни чени еви да |
i ( |
) ≤ bif можнx о экви валентно |
|
|
|
|
|
|
||||||||||||||||||||||||
перепи сатькакограни чени е-равенство спомощ ью |
введени я новой |
|
|
|
|
|
|
|||||||||||||||||||||||||||
переменной u |
i |
: |
i |
( |
) + |
|
2 |
= b . |
u f |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
i |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
Получи тьнеобходи мы е услови я экстремумадля задач |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
3 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) |
|
( |
) → extr ; |
|
f x |
b) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ³ 0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ( |
) ® extr |
|
f |
x |
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4,2) |
|
|
1 ( |
) £ bf |
x, |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
cведя и х кзадачам с |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
.X* |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ограни чени ями -равенствами . |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
7. (З адача Аполлония) Провести и з |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
данной точки кданному элли псу |
|
|
|
|
||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
отрезокми ни мальной дли ны . |
|
|
|
|
|
||||||||||
|
|
1 |
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
8. (З адачаШ т ейнера) Н айти |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
такую |
|
точку вплоскости , чтобы |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Ри с.1 |
|
|
|
|
|
|
|
|
|
|
суммарасстояни й отнеедо трех |
|
|
|
|
||||||||||||||
ми ни мальной. |
|
|
|
|
|
|
|
|
|
|
|
|
заданны х точекбы ла |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
9. Н айти расстояни еотточки впространстве Rn |
до заданной прямой. |
|
|
|
|
|
||||||||||||||||||||||||||||
|
§ 2. Гр а фическо е р еш ение за да ч нелинейно го |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
пр о гр а ммир о в а ния. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Е сли |
допусти мое множество |
W Ì R2 , |
|
то задача опти ми зац и и , |
как |
|
|
|
|
|||||||||||||||||||||||
прави ло, можетбы тьреш енаграфи чески . |
|
|
|
|
|
|
|
|
|
|
2 )(= C, , |
|
|
|
|
|||||||||||||||||||
|
|
Опр еделение. |
|
К ри вы е, |
задаю щ и еся |
|
уравнени ями |
1 |
xf |
x |
|
|
||||||||||||||||||||||
назы ваю тся ли ни ями уровня функц и и |
|
1 xf2 )(x. , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
П р имер 1. Реш и тьграфи чески задачу нели нейного программи ровани я |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
2 |
2 |
2 →x min,− 4 |
+=x |
) −yf |
x ( |
) |
|
( |
)( |
, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
2 |
£ |
1, ) |
( |
3x |
|
x |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
2 £ 2), 4( x x2 |
|
|
|
|
|
|
|
|
|
|
||||||||
12
1 , 2 ³ 0x x
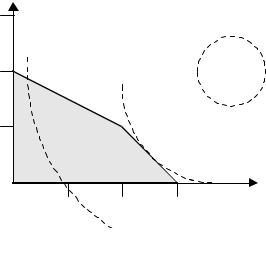
Р ешение: Д опусти моемножество задачи и зображено нари с.1 Л и ни ями уровня ц елевой функц и и являю тся конц ентри чески еокружности с
ц ентром в |
точке (4,2). |
М |
и ни мальному значени ю |
ц |
елевой функц и и |
соответствует окружность |
ми ни мального ради уса, |
пересекаю щ ая |
|||
допусти мую |
область. Т акая окружностьбудеткасаться |
грани ц ы области на |
|||
прямой (1). Д альнейш ееуменьш ени еради усапри води ткли ни ям уровня, не и мею щ и м общ и х точексобластью .
К оорди наты точки касани я можно найти , при равни вая значени я прои зводны х
(x2 )'x |
и з уравнени й прямой |
и |
|
окружности . Д и фференц и руя |
уравнени е |
|||||||||||||||||||
1 |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
окружности |
|
1 |
2 |
= C, |
|
− 2и )рассматри+x (x ( 4 вая) |
x2 |
как неявную |
||||||||||||||||
функц и ю от x1, |
получи м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(x2 )'x |
|
|
( |
1 |
− 4) 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 )'x |
|
|
|
||
= - |
|
|
|
. И з |
уравнени я |
|
прямой |
|
находи м |
=-1. В и тоге |
||||||||||||||
|
( |
|
|
|
|
|||||||||||||||||||
1 |
|
|
2 - 2) 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вы пи сы вается |
равенство: |
1 -- = |
( |
1 |
− 4) 2 x |
т.е. |
|
2 − |
= 1 − 4 . |
xxД обави2 |
в |
|||||||||||||
|
|
, |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
( 2 - 2) 2 x |
|
|
|
|
|
|
|
|
|
|
|||||
уравнени епрямой, которой при надлежи тточкакасани я, |
получи м си стему: |
|||||||||||||||||||||||
ì 1 + |
2 = x3, |
|
x |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
1 |
|
|
|
|
|
|
|
í |
1 -x2 |
. Е ереш ени ем является точка X* = ( |
|
, |
|
) . |
|
|
|
|
|
|||||||||||||
2 |
2 |
|
|
|
|
|
||||||||||||||||||
î 2 = |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
П р имер 2. |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 ® extr-, |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
2 2 |
|
|
=+ |
4) - x ( |
2) |
|||||||
|
|
|
|
|
|
|
− 1 + 2 ≤ |
, |
|
1) ( |
|
|
x4 |
|
x |
|
|
|
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 ³- 2),+0( |
|
|
x 25 |
9x |
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 , |
|
2 ³ 0x |
x |
|
|
|
|
|
|
|
|
|
|||
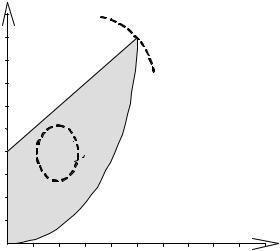
Р ешение: Д опусти моемножество задачи и зображено нари с.2. Л и ни ями уровня ц елевой функц и и являю тся конц ентри чески е элли псы с ц ентром в
точке(2,4) и задаю щ и еся уравнени ем
x2 |
. |
Xmax |
.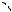
Xmin
x1
Ри с 2.
1 |
2 |
2 |
)2 = C( .( Поскольку− 4) +x |
|
точка |
(2,4) |
при надлежи т |
||
допусти мому множеству, |
то она и |
|||
будет |
являться |
точкой |
ми ни мума |
|
задачи . |
И з |
графи ка ви дно, что |
||
макси мальному |
значени ю |
функц и и |
||
соответствует |
|
элли пс, |
||
пересекаю щ и й |
грани ц у |
области в |
||
точке X max .
К оорди наты этой точки находятся и з услови я пересечени я прямой и
параболы : |
ì- |
1 + 2 |
= x4 |
x |
í |
2 |
|
, |
|
|
î |
2 |
=-0 x+ 25 |
|
|
1 |
|||
откуда 1 = |
, 2 |
= 9. x |
x 5 |
|
x 2( |
)(x |
2 2 x
9x
