
Metody_optimizatsii
.pdf
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
15.Положи м k = 4 . Перейти кш агу 2. |
|
|
|
|
|
|
|
|
|
|
||||||
16. В ы чи сли м f ¢ x4 = |
×10−8(.9 ) |
|
|
|
|
|
|
|
|
|
|
|||||
17. Поскольку |
|
f ′ x3 |
|
|
< ε = 10−7 , (проц) есспои сказаканчи вается. В |
качестве |
|
|||||||||
|
|
|
||||||||||||||
реш ени я задачи при ни мается точка x* |
x4 |
|
|
−8 » 0. =×9 10= |
|
|
|
|||||||||
Бы страя |
сходи мость метода Н ью тона для |
|
рассмотренного |
при мера |
|
|||||||||||
объ ясняется |
|
хорош и м вы бором начального |
|
при бли жени я |
x0 . |
Е сли , |
|
|||||||||
напри мер, для данной функц и и в качественачального при бли жени я вы брать |
|
|||||||||||||||
x0 = 3 , то методом будетгенери роваться последовательностьточек |
|
|
|
|||||||||||||
|
|
|
|
|
|
4 |
|
|
|
8 |
x |
|
× |
18 ;-...x =, |
10 × 27xx, 1= |
|
которая расходи тся. |
|
|
|
13 5 |
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
З а да чи для са мо сто ятельно го р еш ения |
|
|
|
|
|
||||||||
1. Разли чны ми |
|
чи сленны ми методами |
одномерной |
ми ни ми зац и и |
(метод |
|
||||||||||
перебора, |
метод делени я отрезкапополам, метод золотого сечени я, |
метод |
|
|||||||||||||
хорд, метод Н ью тона) найти реш ени еследую щ и х задач. |
|
|
|
|
|
|||||||||||
1) |
3 |
|
|
|
|
|
x* = |
8241x; |
,Î0 |
x |
], ®1, 0[= x f- x |
min, |
||||
2) |
|
|
|
|
|
|
|
x |
* |
- =3855x; |
, 0- Î |
4 |
2 |
|||
|
|
|
|
|
|
|
|
x], 0, 1®x [ + x +=f x m+ |
||||||||
3) ( ) |
e xf |
|
x1 |
|
x |
x* = |
7035 ; |
, 0 |
|
], 15,,5=;→0[+ |
min, |
|||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||
4)
5)
6)
2 |
−x |
x* = 3517x ; ,Î0 |
],e ®1,=0[x |
f+ x |
min, |
|
2 |
|
x* |
- =8354x; |
, 0- Î x |
], |
0;1x®[ x =f+ x +mi |
2 |
− x |
x* = |
7388x. ,Î0 |
],e ®1;x0[ =+x f- x min, |
||
2. |
М ожет ли |
при менени е |
методов и склю чени я отрезков |
при вести к |
|
|
неверному |
определени ю |
x* , если функц и я |
f (x) |
не является |
|
уни модальной? О тветпоясни тьри сунком. |
|
|
||
3. |
Т ребуется |
найти точку ми ни мума уни модальной |
функц и и на отрезке |
||
|
дли ны 1 сточностью ε = 0,02 . И меется возможностьи змери тьнеболее10 |
||||
значени й функц и и f (x) . К акой и з прямы х методов ми ни ми зац и и можно
и спользоватьдля этого?
4.У казатьклассфункц и й, для которы х точноеопределени еточки ми ни мума гаранти ровано врезультатевсего одной и терац и и методаН ью тона?
М ето ды безусло в но йминимиза ции в Rn
Д ля чи сленного реш ени я задачбезусловной ми ни ми зац и и ви да
f x → min ( )
x Rn
разработано много алгори тмов, и спользую щ и х и терац и онны епроц едуры
+ |
= |
k |
k 1 k |
k |
-направлени епои скаточки x |
k+1 |
|
k |
|
|
+ α k yx , гдеx y |
|
|
и з точки x , а |
|||
чи сло α k |
- вели чи наш агаввы бранном направлени и . Работатаки х |
|
||||||
алгори тмовнакаждой и терац и и прои сходи тпо следую щ ей схеме: |
|
|||||||
34
Ш аг1. Провери тьуслови я остановаи , если они вы полнены , вы чи слени я
прекрати тьи взятьточку x k |
в качествеи скомого реш ени я. |
||
Ш аг2. |
Зафи кси роватьненулевой векторy k вкачественаправлени я |
||
|
пои ска. |
|
|
Ш аг3. В ы братьчи сло αk − вели чи ну ш ага. |
|||
Ш аг4. |
Положи ть + = k |
+kα1k yxk |
x |
Д ля проверки услови й останованаш аге1 напракти кечасто и спользую тся следую щ и екри тери и :
|
||xk+1 - xk||< ε |
, |f(xk+1) - f(xk)|<ε |
, |
||Ñf (x k ) |
||<ε , |
|
|
|
||||||
где ε - |
заданны й |
параметр точности . |
К роме того, |
при |
практи ческой |
|||||||||
реали зац и и эти |
|
алгори тмы |
полезно дополнять "дежурны м" |
кри тери ем |
||||||||||
останова k ≤ N max |
, |
где N max − задаваемое заранее макси мальное чи сло |
||||||||||||
и терац и й. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В качестве вектора y k |
на ш аге 2 |
могут вы би раться |
еди ни чны е |
орты |
||||||||||
(покоорди натны й спуск), |
анти гради ент в точке xk (гради ентны е методы ) и |
|||||||||||||
други е направлени я. |
В ели чи на ш ага |
αk , |
как прави ло, вы би рается так, |
|||||||||||
чтобы |
вы полнялось |
услови е |
|
+ |
≤ |
|
xkf) . (( kfВ 1x)частности , |
чтобы |
||||||
гаранти ровать |
вы полнени е |
этого |
неравенства, |
можно |
вы би рать |
|||||||||
αk = |
k |
+ α y k ) ( f будеx м (в |
дальнейшmin |
еargм это назы вать прави лом |
||||||||||
α |
|
|
|
|
|
|
|
|
|
α k |
|
|
|
|
наи скорейш его |
спуска). |
Д ля |
чи сленного |
оты скани я |
может бы ть |
|||||||||
и спользованоди ни з методов, опи санны х впреды дущ ем параграфе. Рассмотри м при меры алгори тмов, построенны х всоответстви и с
предложенной схемой.
Мето дпо ко о р дина тно го спуска .
Этотметод заклю чается впоследовательной ми ни ми зац и и ц елевой
функц и и f(x) сначалапо направлени ю первого бази сного векторае1 ,затем второго е2 и т.д. Т аки м образом, здесь y k = ek , α k вы би рается в
соответстви и справи лом наи скорейш его спуска. Послеокончани я
ми ни ми зац и и по направлени ю последнего бази сного вектораеn ц и клможет повторяться. М етод покоорди натного спускаможетбы тьметодом нулевого порядка, т.к. онможетнеи спользоватьвработепрои зводны х функц и и f(x). Т аки м образом, онможетпри меняться для опти ми зац и и неди фференц и руемы х функц и й.
Алго р итм.
Шаг0. В ы братьначальноепри бли жени ех0 впространствеRn , задатьпараметрточности ε . Н айти f(x0),положи тьj=1.
Шаг1. Pеш и тьзадачу одномерной ми ни ми зац и и
Ф (α )=f(x0+ α |
35 |
ej)→ min , т.е. найти α *. |
|
|
αR |
Положи тьх1=х0+ α *еj, вы чи сли тьf(x1).
Шаг2. Е сли j<n, то положи тьх0=х1, j=j+1 и перейти кш агу 1, и наче кш агу 3.
Шаг3. Провери тьвы полнени екри тери я останова (напри мер, ||x0-x1||< ε
или |f(x0)-f(x1)|<ε ). Е сли онвы полняется, то положи ть x*=x1, f*=f(x1) и
закончи тьпои ск. И начеположи ть х0=х1, f(x0)=f(x1), j=1 и перейти кш агу
1.
Замечани е. Д ля при бли женного реш ени я вспомогательной задачи одномерной ми ни ми зац и и наш аге1 алгори тманапракти ке, какправи ло, и спользую тся методы нулевого порядка(метод перебора, делени я отрезка пополам, золотого сечени я).
Э ффекти вностьметодапокоорди натного спуска сущ ественно зави си т отсвойств ц елевой функц и и . Е сли функц и я сепарабельная, т.е. представи ма
вви де |
n |
x |
)f, т(о череxз )nf(шxагов,.., алгори тма находи тся |
= å |
|||
|
i=1 |
i |
i 1 n |
|
|
|
опти мальноереш ени е.
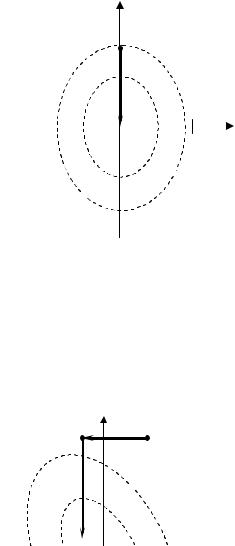
П р имер 1. Реш и тьзадачу покоорди натного спуска.
x1  x0
x0
x* 3
2 |
x2=→xmin+f методомx |
2( |
) |
|||
1 |
2 |
|
|
|
|
|
Реш ени е. |
|
|
|
|
|
|
Д анная |
|
функц и я |
|
является |
||
сепарабельной. |
|
В ы берем |
||||
прои звольную |
начальную |
точку, |
||||
напри мер, |
x0=(3,3). В |
результате |
||||
ми ни ми зац и и по направлени ю |
e1 , |
|||||
очеви дно, |
получается |
точка |
||||
x1=(0,3), а |
ми ни ми зац и я |
по |
||||
направлени ю |
e2 при води т |
к |
||||
опти мальному реш ени ю |
x*=(0,0). |
|||||
П р имер 2. Реш и тьзадачу |
2 |
2 |
1 x2x→ minx =+методомx +f x |
2( ) |
1 |
2 |
покоорди натного спуска. Реш ени е.
0.Задади м x0=(0.5,1), f(x0)=2. В качествекри тери я остановавы берем кри тери й |f(x0)-f(x1)|<ε и задади м ε =0.1.
1.В качествепервого направлени я вы би раем e1. Реш и м задачу одномерной
ми ни ми зац и и по α : |
2 |
α → + . |
αmin+ |
+ Φ) .=5 0( ) .5 |
|||
|
|||||||
x |
1 |
1 |
x0 |
|
α*=-0.75, х1=(-0.25,1), f(x1)=0.375. |
||
|
|
|
2. Полагаем х0=х1 . |
|
|
||
3. В качествеследую щ его направлени я вы би раем е2. Запи сы ваем задачу

36
одномерной ми ни ми зац и и :
|
|
|
2 |
α ®α + . |
minα- F+) |
= 1 |
|
|
|
|
|
||||
|
|
|
α *=-0.875. |
|
|
|
|
|
|
|
х1=(-0.25,0.125), f(x1)=0.11. |
|
|
|
|
0,5 |
|
|
|
|
|||
|
|
|
4. Проверяем кри тери й останова: |
|
|
|
|
|
|
|
|0.375-0.11|=0.265>ε |
|
|
|
|
|
|
|
5. В качестве направлени я снова |
|
|
|
|
|
|
|
вы би раем e1. Реш и м задачу |
|
|
|
|
|
|
2 |
одномерной ми ни ми зац и и по α : |
|
|
||
|
|
α ®α + . |
-min |
α+) |
+25 .F0-( |
=1 |
|
|
|
|
|||||
α* ≈ 0.22. х1=(-0.03,0.125), f(x1) ≈ 0.021.
6.Полагаем х0=х1 .
7. В качестве направлени я вы би раем е2. |
Запи сы ваем |
задачу одномерной |
|
ми ни ми зац и и : |
2 |
α |
®α + . min α- ) + F125 =. |
|
|||
α*=-0.11. х1=(-0.03,0.015), f(x1) ≈0.001.
4.Проверяем кри тери й останова: |0.021-0.001|=0.02<ε . Полагаем x*=(-0.03,0.015), f*=0.001.
Замечани е. И з графи ческой и ллю страц и и ви дно, что опти мальны м реш ени ем является ц ентрконц ентри чески х элли псовточка(0,0) .
М ето ды гр а диентно го по иска .
Представленны едалееметоды и спользую туслови еди фференц и руемости функц и и f(x) вRn. В качествекри тери я остановатаки х методов, какправи ло,
вы би рается услови е||Ñf (x k ) ||<ε . В качественаправлени я дви жени я для оты скани я ми ни мумавметодах гради ентного спусканакаждом ш аге
вы би рается векторанти гради ент k =y-Ñ (x k f) . К аки звестно, вмалой
окрестности точки xk анти гради ентобеспечи ваетнаи скорейш ееубы вани е функц и и . При ведем двавари антаметодовгради ентного спуска (отли чаю щ и еся способом оты скани я вели чи ны α ).
А лго р итм мето да др о бления ш а га .
Ш аг0. Задатьпараметрточности ε , начальны й ш аг α > 0, вы брать
х0 ÎRn ,вы чи сли тьf(x0).
Шаг1. Н айти Ñf (x0 ) и провери тькри тери й останова: ||Ñf (x0 ) ||<ε .
Е сли онвы полнен, то вы чи слени я заверш и ть, полагая x*=x0, f*=f(x0) .
Ш аг2. |
Положи тьх1=х0- α Ñf (x0 ) , вы чи сли тьf(x1). Е сли f(x1)<f(x0), |
||||||
|
то положи тьх0=х1 , f(x0)=f(x1) и перейти кш агу 1. |
|
|||||
Ш аг3. |
Положи тьα = α |
2 |
и перейти кш агу 2. |
|
|||
|
|
|
|
2 |
x2=®xmin+f методомx |
|
|
П р имер . Реш и тьзадачу |
гради2( ентного) |
||||||
спуска. |
|
|
|
|
1 |
2 |
|
|
|
|
x 2).x 4, f |
x( ( |
|
|
|
Реш ени е. Ñ |
= |
1 |
) |
|
|||
|
|
|
2 |
|
|
|
|
И т ерация1.

|
Задади м x0=(0.5,1), f(x0)=1.5. |
37 |
2. |
В ы берем ε =0.01, α = 1 . |
|
3. |
Ñf (x0 ) =(2, 2), ||Ñf (x0 ) ||>ε . |
|
4. |
Положи м х1=х0- Ñf (x0 ) =(0.5 -2, 1-2)=(-1.5,-1), f(x1)=5,5, f(x1)>f(x0). |
|
5.Положи м α = α 2 =1/2 и перейдем кш агу 2.
6.Положи м х1=х0- 12 Ñf (x0 ) =(0.5 -1, 1-1)=(-0.5,0), f(x1)=0.5. Т аккак
|
f(x1)<f(x0), то полагаем х0=х1=(-0.5,0) , f(x0)=f(x1)=0.5 и переходи м кш агу |
||||
|
1. |
|
|
И т ерация2. |
|
|
|
|
|
||
7. |
Ñf (x0 ) =(-2,0), ||Ñf (x0 ) ||>ε |
||||
8. |
Положи м х1=х0- |
|
1 |
Ñf (x0 ) =(-0.5 +1, 0)=(0.5,0), f(x1)=0.5, f(x1)=f(x0). |
|
2 |
|||||
|
Положи м α = α |
|
|||
9. |
2 |
=1/4 и перейдем кш агу 2. |
|||
|
|
|
|||
10.Положи м х1=х0- 41 Ñf (x0 ) =(-0.5 +0.5, 0)=(0,0), f(x1)=0, f(x1)<f(x0).
Полагаем х0=х1=(0,0) , f(x0)=f(x1)=0 и переходи м кш агу 1.
11.Ñf (x0 ) =(0,0), ||Ñf (x0 ) ||=0<ε - останов, найдено точноереш ени е.
Алго р итм мето да на иско р ейш его спуска .
Шаг0. Задатьпараметрточности ε , вы братьх0 ÎRn .
Шаг1. Н айти Ñf (x0 ) и провери тькри тери й останова: ||Ñf (x0 ) ||<ε .
Е сли онвы полнен, то вы чи слени я заверш и ть, полагая x*=x0, f*=f(x0) .
|
Ш аг2. Реш и тьзадачу одномерной опти ми зац и и |
|
|
|
|
|
|||||
|
Ф (α )=f(х0- α |
Ñf (x0 ) ) ® min , т.е. найти α *. |
|
|
|
|
|||||
|
|
|
|
α > |
0 |
|
|
|
|
|
|
|
Положи тьх0=х0- α *Ñf (x0 ) |
и перейти кш агу 1. |
|
|
|
||||||
П р имер 1. |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
Реш и тьзадачу |
1 |
x 2 ® minx 4 -методомx -= x f+ x |
( |
) |
||||||
|
|
|
1 |
2 |
2 |
|
|
|
|
|
|
наи скорейш его спуска. |
|
- 2) |
x2 4, |
x2 |
f( (x) |
|
|
|
|||
|
Реш ени е. Ñ |
= 1 - |
2 |
|
|
|
|||||
|
|
|
|
И т ерация1. |
|
|
|
|
|
||
0.Задади м x0=(4,5). В ы берем ε =0.01. |
|
|
|
|
|
|
|||||
1. |
Ñf (x0 ) =(4, 8), ||Ñf (x0 ) ||>ε . |
|
|
|
|
|
|
|
|
||
2. |
Реш и м задачу одномерной ми ни ми зац и и по α : |
|
|
|
|
|
|||||
|
f(х |
0 |
|
|
|
0 |
2 |
2 |
+ α(f x- )) |
=α( |
Ñ -F( |
|
|
|
|
|
8α)5 - |
( 4α- )4 |
|||||
|
|
α |
8α 5®2 |
-.4 4 min4− |
- ) |
( |
( ) |
|
|
|
|
α*=0.5. х0=х0- α *Ñf (x0 ) =(4-4·0.5, 5-8·0.5)=(2,1).
Ит ерация2.
3.Ñf (x0 ) =(0,0), ||Ñf (x0 ) ||=0<ε - останов, найдено точноереш ени е.
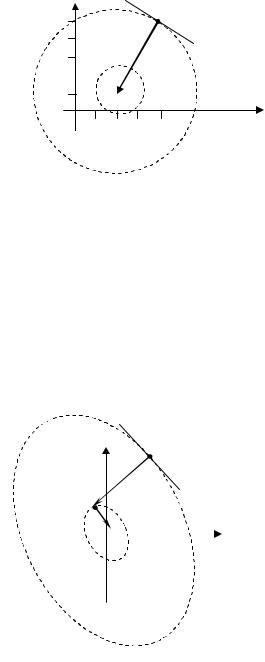
Графи ческая и ллю страц и я реш ени я при ведена на ри сунке. В данном случае ли ни и уровня являю тся конц ентри чески ми
38
x0
Ñf (x0)
.x*
П р имер 2. Реш и тьзадачу
наи скорейш его спуска. Реш ени е.
2 |
2 |
1 x2x® minx =+методомx +f x |
2( ) |
1 |
2 |
Ñ |
= |
+ |
+ x1 ) x122 x2, x 4 f x( ( ) |
|
|
|
|
|
||
|
|
|
|
И т ерация1 |
|
|
|
|
|
|
12.Задади м x0=(0.5,1), ε =0.4. |
|
|
|
|
|
|
||||
13. Ñf (x0 ) =(3, 2.5), |
||Ñf (x0 ) ||=3.9>ε . |
|
|
|
|
|
|
|||
3. Реш и м задачу одномерной ми ни ми зац и и по α : |
|
|
|
|
||||||
|
|
|
|
f(х |
0 |
0 |
2 |
α. f( -x )) |
=α( |
Ñ |
|
|
|
x0 |
|
|
3α)5 0+ 2 |
||||
|
|
|
|
2 |
|
α 5α2 ®1 min3α-5 0) .- 1 5 2)(+ |
+ |
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
α *=0.24.
х0=х0- α *Ñf (x0 ) =(0.5-3·0.24, 1-2.5·0.24)= =(-0.22,0.4).
0.5 |
И т ерация2. |
|
|
|
|
|
|
||
|
4. Ñf (x0 ) =(-0.48, 0.58), ||Ñf (x0 ) ||=0.752>ε . |
|||
|
5. Реш и м задачу одномерной ми ни ми зац и и . |
|||
f(х 0 |
|
058α)02 +4. 0 . ( - α48)2 0+ . 22 .0α+(2 |
||
α |
58α 0®4min0 -48) 0 |
.0 22 +. )(+ - . |
( . |
|
α *=0.546, х0=х0- α *, Ñf (x0 ) =(−0.22 + 0.48α,0.4 − 0.58α) =(0.04, 0.08) |
|
|||
|
И т ерация3. |
0 Þ= = |
|
|
14. Ñf (x0 ) =(-0.24, 0.2), ||Ñf (x0 ) ||=0.312<ε |
08).*0. |
04, . 0(x x |
||
Заданная точностьдости гнута, однако опти мальноереш ени я |
minx= ( |
,0)0за2 |
||
и терац и и найдено небы ло. И з графи ческой и ллю страц и и ви дно, что ли ни ями уровня вданной задачеявляю тся конц ентри чески еэлли псы и получаемы ев ходеалгори тманаправлени я непроходятчерез и х ц ентр.

39 |
|
|
|
|
|
|
|
|
|
Д ажедля квадрати чны х |
функц и й сходи мостьгради ентны х |
|
|
||||||
методовзаконечноечи сло и терац и й негаранти рована. О днако если |
|
|
|
|
|
||||
квадрати чная функц и я n переменны х при веденакви ду суммы полны х |
|
|
|
||||||
квадратов, то ееопти мум можетбы тьнайденврезультатереали зац и и n |
|
|
|
||||||
одномерны х пои сковпо преобразованны м коорди натны м направлени ям. |
|
|
|
||||||
Проц едурапреобразовани я квадрати чной функц и и |
( ) |
T + |
1=xHx+T |
к |
|||||
|
|
|
|
|
2 |
|
|
|
|
ви ду суммы полны х квадратовэкви валентнанахождени ю |
такой матри ц ы |
|
|
|
|||||
преобразовани я Q, которая при води тматри ц у квадрати чной формы к |
|
|
|
||||||
ди агональному ви ду. Т аки м образом, заданная квадрати чная форма xHxT |
|
|
|
||||||
путем преобразовани я x=zQ при води тся кви ду xHx |
T |
= |
= |
|
z |
T |
|
T |
|
|
|
|
,zD |
||||||
где D -ди агональная матри ц а. Пусть q j |
− j - тая строкаматри ц ы Q. Т огда |
|
|
||||||
преобразовани еx= zQ позволяетзапи сатькажды й векторx в ви дели нейной
комби нац и и векторов q j : x= zQ= |
1 |
1 |
2 + .. + +qnz. Д руги миq zсловамиz q , |
|
2 |
n |
осущ ествляется переход кновой си стемекоорди нат, задаваемой векторами q j ( замети м, что это преобразовани енеявляется еди нственны м). Т аки м образом, спомощ ью преобразовани я переменны х квадрати чной функц и и
о о р дина т , со в п а да ю щ их с гла в ны мио сям и
квадрати чной функц и и . Следовательно, одномерны й пои скточки ми ни мума впространствепреобразованны х переменны х экви валентенпои ску вдоль каждой и з главны х осей квадрати чной функц и и . Д ля полученной си стемы
векторов q j будутвы полняться равенства i |
j |
T = |
¹ j. i |
, 0( |
|
) qq H |
||||||
О пред ел ение. Си стемали нейно незави си мы х векторов q j , для которой |
|
|
||||||||||
вы полняю тся равенства i |
j |
T = |
, 0(¹ j), назыi |
ваетсяqсиq стемойH |
H- |
|
|
|||||
сопряженны х направлени й. |
|
|
|
|
|
|
|
n1 |
2 |
|||
И так, если заданы лю бы еn H-сопряженны х направлени й |
, ..q |
|||||||||||
|
, qто |
|||||||||||
проц едура + = |
k |
+kα1k qxk , гдеxα k = |
α |
k |
+ α qk ) ,f kx= 1,2...(n , |
|
min |
|||||
|
|
|
|
|
|
|
|
|
|
|
||
позволяетнайти ми ни мум квадрати чной функц и и . |
|
|
|
|
|
|||||||
Т аккакдостаточно больш ой классц елевы х функц и й можетбы ть |
|
|
||||||||||
представленвокрестности точки ми ни мумасвоей квадрати чной |
|
|
|
|||||||||
аппрокси мац и ей, опи санная и дея при меняется и для неквадрати чны х |
|
|
||||||||||
функц и й. |
|
|
|
|
|
|
|
|
|
|
|
|
Построени е си стемы H- сопряженны х направлени й возможно |
|
|
||||||||||
разли чны ми способами . Рассмотри м некоторы еи з ни х. |
|
|
|
|
||||||||
М ето дсо пр яжённы хна пр а в ленийП а уэлла |
|
|
|
|||||||||
И терац и онны й |
проц есс |
в |
методе |
Пауэлла |
органи зуется |
|
без |
|||||
предвари тельного |
|
построени я |
H- |
сопряженны х |
векторов, |
которы е |
||||||
последовательно |
находятся |
в |
проц ессе ми ни ми зац и и |
с и спользовани ем |
||||||||
свойствапараллельного подпространства.
bx a
T HQz
arg
У т верж д ение ( |
40 |
|
|
свойст во парал- |
лельного подпрост ранст ва). |
Е сли |
|
точка y1 найденав результатепои скаи з точки x1 вдолькаждого и з m (m<n) |
|||
сопряженны х направлени й, а точка y 2 получена в результате пои ска и з |
|||
точки x2 вдолькаждого и з тех же m сопряженны х направлени й 1 , |
2 ..qm ,q |
||
то вектор y 2 − y1 |
задаетнаправлени е, |
сопряженноесо всеми вы бранны ми m |
|
направлени ями . |
|
|||
А лгори тм может бы ть органи зован следую щ и м образом. |
И значально |
|||
полагается |
q j = j ,= |
|
|
|
, 1ne (затj ем эти направлени я будут последовательно |
||||
заменяться |
построенны ми сопряженны ми направлени ями ). |
В води тся |
||
вспомогательноенаправлени е q0 = en . Н аходи тся ми ни мум функц и и f (x) при последовательном дви жени и и з некоторой начальной точки x0 по (n+1)
направлени ям , ,.., q q, прqи этом каждая получаемая точкаи спользуется в
n 0 1
качестве и сходной для пои ска по следую щ ему направлени ю . По свойству параллельного подпространства, направлени е, проходящ ее через точки , полученны епри первом и последнем пои ске, будетHсопряжено сqn . Д алее
заменяется q1 на q2 , q2 на q3 и т.д. В качественаправлени я qn вы би рается полученное сопряженное направлени е, после чего повторяется пои ск по
(n+1) направлени ям (уже не содержащ и м старого направлени я |
q1 ). Д ля |
квадрати чны х функц и й последовательность n2 одномерны х |
пои сков |
при води ткточкеми ни мума. |
|
Алго р итм мето да со пр яжённы хна пр а в лений.
Шаг0. Задатьпараметрточности ε , вы братьх0 Rn , положи тьк =0, i=0 ,
q |
j |
|
|
|
j |
|
n |
00 |
0 |
. j |
|
|
|
|
|
|
|
|
|
||
, , |
, |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
= e=, |
yq |
==nex1 |
|
|
|
|
|
|
|
|
|
||||||||
Ш аг1. Н айти yi+1=yi+ α i qi , где α i = |
α |
i + α qi ) |
f |
y |
( |
min |
|
arg |
|||||||||||||
Ш аг2. Провери тьуслови еi=n . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
а) Е сли оно вы полняется, то вы ясни тьуспеш ностьпои скапо n |
|
|
|
||||||||||||||||||
последни м направлени ям. Е сли yn+1=y1, пои скзаверш и ть, полагая |
|
|
|||||||||||||||||||
x*= yn+1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b) Е сли i<n, |
положи тьi=i+1 и перейти кш агу 1. |
|
|
|
|
|
|
|
|||||||||||||
Ш аг3. Положи тьхk+1=yn+1 и провери тькри тери й останова |
|
|
|
|
|
|
|||||||||||||||
(напри мер, ||x0-x1||< |
ε и ли |
|f(x0)-f(x1)|<ε ). |
|
|
|
|
|
|
|
|
|
||||||||||
Е сли онвы полнен, то вы чи слени я заверш и ть, полагая x*=xk+1 . |
|
|
|
||||||||||||||||||
|
|
|
j |
|
|
+ |
|
|
|
|
|
n+ |
n 1 |
|
1 |
|
1 0 +1 k |
0 |
|
|
|
Ш аг4. Положи ть q |
|
|
|
j |
, 1, |
, 1 |
, |
|
qn= |
j |
|||||||||||
|
|
|
|
|
|
|
|
− y |
|
y= y= x= q,= |
q− |
||||||||||
i=0 , к =к +1 и перейти кш агу 1.
П р имер 2. Реш и тьзадачу |
|
|
|
|
2 |
|
2 |
|
1 x2x→ minx =+методомx +f x |
|
|
|
||||||||||||||
|
|
|
|
1 |
2 |
|
|
|
|
|||||||||||||||||
сопряженны х направлени й. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Р ешение. |
|
|
0 |
= |
|
|
|
|
|
|
|
|
0 |
= e |
2 |
|
= , |
= e |
2 |
102 |
=e |
10 |
= |
|
||
|
В ы берем x |
1 |
1() , положи м |
|
|
1 |
||||||||||||||||||||
0. |
|
q |
|
|
, |
|
, q q |
|
||||||||||||||||||
|
2 |
|
|
|
|
2 |
||||||||||||||||||||
|
1 |
|
|
|
α |
|
|
|
|
+ α |
|
)1.=0y |
= , ( 1+) , ( |
|
|
|
|
|
|
|||||||
1. |
1 |
|
|
0 |
|
|
1 |
1 |
0 |
() , |
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2( )
1() .,y x

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Реш и м задачу одномерной ми - |
|
|
|
|
|
|
|
ни ми зац и и : |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
1 |
|
|
|
|
α ®α min+ |
|
|
α+) |
F+( |
= |
) |
(( |
) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
α0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
) (.= , |
|
|
|
|
Þ= - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
2. Т аккакi<2, |
положи м i=1 и перейдем кш агу 1. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3. |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α1 |
0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α1 - |
|
|
|
) . +, = ( |
|
) =,+( - ) ( , |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Реш и м задачу одномерной ми ни ми зац и и : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
αα® min+ |
|
α-) |
|
|
|
|
|
+F( |
=) |
( |
( |
) |
|
||||||||||||||||||||||||||||||||||||||||
|
|
α1 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
1 |
|
- |
1 |
)(. =, |
|
Þ= - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
4. Т аккакi<2, |
положи м i=2 и перейдем кш агу 1. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5. |
|
|
3 |
y |
1 |
|
|
|
|
1 |
|
|
|
|
|
α2 |
1 0 |
|
1 |
|
|
α2 - |
1 |
). |
=, |
|
( |
)=,+( - )( |
|
, |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
16 |
|
4 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Реш и м задачу одномерной ми ни ми зац и и : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
α ®α min+ - |
|
|
|
)α+ |
(+F - =) |
|
|
|
(( |
) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
4 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
α2 |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
) (.= =, |
|
|
Þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
6. |
|
Т аккак i=2 и y3 ¹ y1 , положи м х1= y3 = |
1 |
|
- |
1 |
) (. |
, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
16 |
|
32 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Положи м q1 = e2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
|
yq-30 |
|
|
|
q(72 |
|
0 = |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7= |
|
)-=, y, |
1 |
- |
1 |
|
) (, |
, |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
32 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i=0 , к =2 и перейдем кш агу 1. |
16 |
|
32 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
y |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
α0 |
7 7 |
|
|
|
|
|
|
|
|
|
|
|
1−7α0 |
|
−1+7α0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
- |
32=+ |
) . |
|
- , |
|
( |
) , |
|
|
( |
) ( , |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
16 |
|
|
|
|
|
|
|
32 |
|
|
|
|
|
16 |
32 |
|
|
|
16 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Реш и м задачу одномерной ми ни ми зац и и : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
α |
2 |
|
|
|
1−7α |
2 |
|
|
|
|
|
|
|
|
|
|
−1+7α |
2 |
|
|
1−7α |
|
|
−1+7α0 |
|
|
0 0 |
|
|
|
|
0 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
® min |
) |
|
|
|
+ )( |
( + ) F ( = |
||||||||||||||
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
32 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
α |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 =y(=,0)Þ0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9. Т аккакi<2, |
положи м i=1 и перейдем кш агу 1. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
10. 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α1 |
|
|
|
|
|
|
|
|
|
= =0 α1)1. 0+, |
(y ) 0, |
0( ( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
Реш и м задачу одномерной ми ни ми зац и и : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
α |
|
|
|
|
|
|
|
α 2 F® min= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
α1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 = = 0()0Þ.0, |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
11. Т аккакi<2, положи м i=2 и перейдем кш агу 1. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
y 0 0 α |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7α 2 |
|
7α 2 |
=) .- , |
+ ( |
|
) , |
|
( ( , ) |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
16 |
|
|
32 |
|
|
|
|
32 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Реш и м задачу одномерной ми ни ми зац и и :
α |
7 |
2 |
7 |
2 |
7 |
7α |
2 |
αα |
α |
2 |
|
|
|||
2 |
|
|
|
|
|
|
|
|
® min |
- |
+ ) F-( = ) |
( ( ) |
|||
16 |
|
32 |
|
16 |
32 |
||||||||||
α2 |
3 = (=,0)Þ0.0 |
y |
|
|
|
|
|
|
|
|
|
|
|||
12. Т аккак i=2 и y3 = y1 , положи м x*= y3 =(0,0).
Графи ческая и ллю страц и я реш ени я при веденанари сунке
x0
1
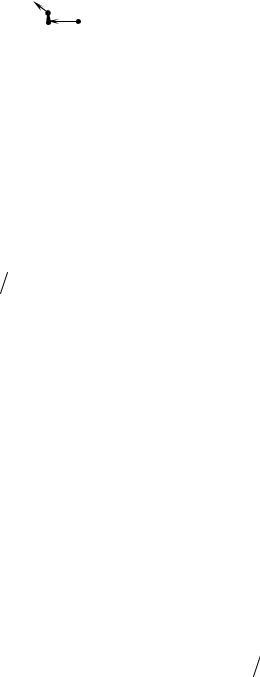
42
x* |
x1 0.5 |
|
y1 |
y2
М ето дсо пр яжённы хгр а диенто в
Д анны й метод позволяетполучать сопряженны енаправлени я pk для
квадрати чной функц и и f(x) си спользовани ем еепрои зводны х. В качестве p0 вы би рается вектор-анти гради ент, аостальны е направлени я вы чи сляю тся по
формуле |
|
pk+1= |
-Ñf (xk +1 ) + |
β k |
pk, |
k = |
|
|
, 0, |
где |
||||||
|
|
n -1 |
||||||||||||||
β k |
k + |
Ñ |
x |
k |
f || |
2 |
|
1 2 |
|
|
|
k +1 |
и меет ви д |
|||
|
|
|
).=Ф(Ñормулf ||x а||пересче) ( та||точки x |
|
||||||||||||
хk+1=хk+ α k pk , при чем ш аг |
α k и щ ется по прави лу наи скорейш его спуска. |
|
||||||||||||||
При |
отсутстви и |
вы чи сли тельны х погреш ностей метод сопряжённы х |
||||||||||||||
гради ентов обеспечи вает оты скани е ми ни мума квадрати чны х функц и й |
не |
|||||||||||||||
болеечем заn и терац и й. Д ля неквадрати чны х функц и й сходи мостьметодаза конечноечи сло и терац и й негаранти рована.
Алго р итм мето да со пр яжённы хгр а диенто в .
Шаг0. Задатьпараметрточности ε , вы братьх0 ÎRn ,вы чи сли тьf(x0).
Шаг1. Положи тьк =0, p0= -Ñf (x0 ) ;
Шаг2. Реш и тьзадачу одномерной ми ни ми зац и и
Ф (α )=f(х |
0 |
k → min |
, т.е. найти α k. |
|
|
|
|
|
|
|
|
|
|
|
+ α p ) |
α >0 |
|
|
|
|
|
|
|
|
|
||
Ш аг3. Положи тьхk+1=хk+ α k pk . |
|
|
|
|
|
|
|
|
|
|
|||
Провери тькри тери й останова: ||Ñf (xk +1 ) |
||<ε . |
|
|
|
|
|
|
|
|
||||
Е сли онвы полнен, то вы чи слени я заверш и ть, полагая |
|
|
|
|
|
||||||||
x*=xk+1, f*=f(xk+1) . |
|
|
|
|
|
|
|
|
|
|
|||
Ш аг4. Провери тьуслови ек +1=n . Е сли оно вы полняется, то положи ть |
|
|
|||||||||||
x0=xk+1, |
f(x0)=f(xk+1) |
и перейти кш агу 1 (обновлени еметода). |
|
|
|||||||||
|
|
|
|
k + |
Ñ |
x |
k |
f |
|| |
2 |
1 |
2 |
( || |
Ш аг5. В ы чи сли тькоэффи ц и ент β k |
|
|
) =и (Ñf ||x |
|| ) |
|||||||||
найти новоенаправлени епои скаpk+1= -Ñf (xk +1 ) + β k |
|
pk . |
|
|
|||||||||
Положи тьк =к +1 и перейти кш агу 2. |
|
|
|
|
|
|
|
|
|
||||
Замечани е1. О пи санны й метод является методом первого порядка, поэтому для реш ени я задачи одномерной ми ни ми зац и и наш аге2 ц елесообразно и спользовать, напри мер, метод хорд, вы би рая вкачествеи нтервалапои скаα отрезок[0,1].
