
Metody_optimizatsii
.pdf
|
|
|
|
Ñf (x) = (2x - 8, 2 y - 4) |
53 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И т ерация1. |
|
|
|
|
|
|
|
|
|||||||
Ω |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
Ñ- 4)-(. 8Рас=, смотри( f )x м задачу |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
.x* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x0. |
|
|
|
|
|
|
|
|
|
ли нейного программи ровани я |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
T |
1 |
x2 ®Ñminx - |
x-f =x4 |
8 |
( |
) |
|||||||
|
|
|
|
|
|
|
|
|
.x1 |
Реш и вееграфи чески , получаем |
Ω |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
0 |
= |
|
|
|
0 |
= |
,0)3, |
1 |
α0),3(x0(,), где3, α |
|
= |
|
min f |
αrg) .0, |
(3 |
|
|
|
|
|
||||||||||
min |
|
|
|
|
|
(x =l |
0 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0£α£1 |
|
|
|
|
|
|
|
|
|||
Запи ш ем задачу одномерной опти ми зац и и |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
α - |
2 ® min |
|
) 4 |
(3 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 £ α £1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Реш ени ем этой задачи будетα 0 |
|
|
тогда , 1 = |
min0 = |
0)3=, |
(1 |
x |
x |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
И т ерация2 |
T |
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
Ñ- 4)-. Ра2=,ссмотри(f x) м задачу |
|
|
1 |
|
1 |
x2 ® minÑx - |
|
x-f =x4 |
2 |
( |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
Реш ени ем этой ЗЛ П является отрезок, соеди няю щ и й точки (2,1) и (0,2). |
|
|
|
|
|
|||||||||||||||||||||||||
В ы берем одну и з ни х, напри мер, |
xmin1 |
=(2,1). Т огда l0 |
|
|
− =1)1,, |
(−,0)3 |
(2 1() , |
|
|
|||||||||||||||||||||
x2 = 3 -α1 (α1) . |
Запи, |
ш ем задачу одномерной опти ми зац и и |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
α |
2 |
|
|
α |
2 ® min- |
+ -) 2- |
|
(( |
|
|
)1 |
|
|
|
|
|
|
|
|
||||||||
|
0 £ α £1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
Реш ени ем этой задачи будетα0 = |
тогда |
= |
2) 1/2, 5/ ( |
x |
1 / 2, |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
И т ерация3. |
T |
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
Ñ- 3)-. Ра3=,ссмотри((f x) м задачу |
|
|
2 |
|
1 |
x2 ®Ñxmin- |
x-f =x3 |
3 |
( |
) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
Реш ени ем этой ЗЛ П является отрезок, соеди няю щ и й точки (2,1) и (3,0). |
|
|
|
|
|
|||||||||||||||||||||||||
В ы берем одну и з ни х, напри мер, |
xmin2 |
=(3,0). Т огда |
|
|
|
|
|
|
|
|
||||||||||||||||||||
l2 |
|
|
|
α2 |
|
|
|
α2 |
|
− 2) .1=/ 2, 1=/ ( 2)−1/2, 5/ ((3,0) |
|
|
|
|
|
|
|
|
||||||||||||
x2 = (5 |
+ |
, 1 − |
|
) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Запи ш ем задачу одномерной опти ми зац и и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
3 |
2 |
α |
|
|
3 |
|
2 ® min-+ |
+ ) |
( ( |
) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
0 £ α £1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Реш ени ем этой задачи будетα 2 |
|
0, тогда= 3 |
x 2 = |
= |
) .2/О 1,станов2/ 5( . |
|
x |
|
|
|||||||||||||||||||||
Получено опти мальноереш ени ех*=(5 / 2,1/ 2) . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
М ето дсекущ ихпло ско стей
Д анны й метод при меняется для реш ени я задач вы пуклого программи ровани я сли нейной ц елевой функц и ей :
cxT ® max |
54 |
||
(1) |
|||
i |
i W = |
,m1 |
£,i :b)f (x |
Замечани е 1. Л ю бая задача вы пуклого программи ровани я может бы ть запи санавви де(1).
Действи тельно, если естьзадачаснели нейной ц елевой функц и ей
ϕ(x) → max
|
|
|
|
|
i |
|
£ i |
= |
|
m |
, ,i1 b,f x( ) |
|
|
|
|
|||||||
то онаможетбы тьперепи санаследую щ и м образом |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
μ → max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
μ - ϕ x £ 0( ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
£ i |
= |
|
|
,i (b)f x |
|
|
|
|
||||||||
|
|
|
|
|
i |
, m1 |
|
|
|
|
||||||||||||
М етод секущ и х |
плоскостей |
основан на при бли жени и |
всех |
нели нейны х |
|
|||||||||||||||||
функц и й |
fi (x) |
ли нейны ми |
|
|
с и спользовани ем разложени я по формуле |
|
||||||||||||||||
Т ейлора. |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 T |
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x f )f x( |
( ) |
|||||||
|
|
|
|
|
|
|
i |
i |
|
|
- x |
») x |
xÑ+)(f |
|||||||||
Рассмотри м задачу |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||||||
cxT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
® max |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
||||
|
|
|
|
|
|
|
0 0 T |
|
|
|
i 0 = |
|
|
|
|
|
|
|
||||
|
1 |
i |
i |
|
|
|
|
|
|
, m1 |
£,i |
b -W) |
x )(x Ñ+x( f |
:)f x( |
||||||||
Е сли |
множество Ω1 ограни чено, то задача(2) всегдаразреш и ма(в |
|
||||||||||||||||||||
проти вном случаеможетоказаться, что sup cxT |
= +¥, дажеесли задача(1) |
|
||||||||||||||||||||
разреш и ма) |
|
|
|
|
|
|
|
Ω1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
fi (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т аккакфункц и и |
вы пуклы вни з, справедли во неравенство |
|
|
|
||||||||||||||||||
|
|
i i |
0 |
0 |
) |
T |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
- |
|
|
|
i |
|
|
£ bi . )(Следовательно-x(£ x )xÑ+f(Ω ( )Ωx1 . fПустьf x x |
|
|
|||||||||||||||
реш ени езадачи (2).
1)Е сли точка x1 допусти мавзадаче(1), то онаявляется опти мальны м
реш ени ем этой задачи (поскольку это экстремум той жец елевой функц и и наболееш и роком множестве).
2) Е сли |
x1 ÏW, то взадаче(2) добавляю тся новы ели нейны еограни чени я: |
|||||
|
T |
1 |
|
1 1 |
1 |
+тxÑ)(f (f x( ) |
i |
i |
|
> b }.Э xти) fограни( i {:£чениb , |
я -обладаюx ) x |
||
|
ii |
i |
|
|
||
следую щ и ми свойствами :
a)точка x1 неудовлетворяетэти м ограни чени ям;
b) во всех точках множестваΩ они вы полняю тся.
Т аки м образом, получаем новоемножество Ω2 , такоечто Ω Ω2 Ω1.
Д алееи терац и онны й проц ессповторяется. Д оказано, что генери руемая таки м
образом последовательность{ xk } реш ени й ЗЛ П сходи тся копти мальной точкеи сходной задачи . А лгори тм методаи меетследую щ и й ви д.
|
|
|
55 |
|
|
|
|
|
|
А лго р итм мето да секущ ихпло с- |
|
|
ко стей |
||||||
Ш аг 1. Задать x0 (не обязательно допусти мое), |
ε |
(точность попадани я в |
|||||||
допусти мую область). |
|
|
|
0 |
0 T |
|
0 = |
|
|
Ш аг2.Положи ть |
|
|
|
|
|
} £,i1 b, - x) x Ñ |
|||
1 |
i |
i |
i |
m |
|||||
Ш аг3. Н айти |
|
xk - реш ени езадачи ли нейного программи ровани я |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
cxT ® max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ÎWk |
|
|
|
|
|
|
|
|
|
|
Ш аг4. |
Е сли |
|
|
|
k"): |
b( |
£ ε xi -,f то останов x* = xk |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
Ш аг5. Положи ть |
k |
|
k |
T k |
|
|
|
k > b }; x) f (i |
|||||||||||
|
|
|
+1 |
|
|
|
i |
ki |
|
|
i |
||||||||
|
|
|
|
|
|
k |
|
i |
|
|
i |
|
|
|
|
||||
|
|
|
k=k+1 . Перейти кш агу 3. |
|
|
|
|
|
|
|
|
|
|
||||||
П р имер 1. Реш и тьметодом секущ и х плоскостей задачу |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
ϕ |
= 1 + x2 ®xmax |
|
|
( |
) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
x2 |
x-1£ f +x = -2 ( ) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
x= £ 9 x + 2f x .8 0( ) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
Р ешение. В ы берем x0 = |
x1, x2 ³ 0 |
|
|
|
|
|
|
|
|
|
|
||||||||
) .4,(В5ы чи сли м Ñ 1 |
= - |
x2 ) , |
2;f 2 x( ( ) |
|
|
|
|||||||||||||
Ñ |
2 |
|
= |
x |
|
)f.2;Т xогда6. 1( ( |
) |
|
|
|
|
T |
|
x |
2 |
-16x |
1 |
+ |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
x 2 |
- 20x 1 2 + |
2 = |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
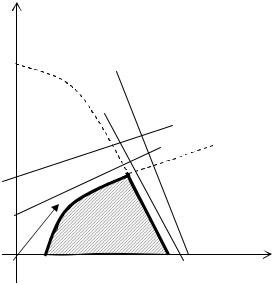
Реш и м графи чески задачу ли нейного |
|
|||||||||
|
|
|
|
|
|
|
|
|
программи ровани я |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
x1 + x2 → max |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
x2 £-15ü2 + 8 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
x + |
x |
2 |
£ 29 8ý W12 |
|
|
|
|
|
|
|
|
|
|
|
· x1 |
|
|
|
1 |
|
|
þ |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x1, x2 ³ 0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
x2 |
|
Е ереш ени ем является точка |
|
|
|
|
|||||||
|
|
|
|
|
|
· |
|
|
x1 = |
) . О62днак. 2; о97вэтой.(2 точке |
|
||||||||
|
|
|
|
|
|
· |
|
|
|
||||||||||
Ñϕ |
|
|
x* |
|
наруш аю тся первоеи второе |
|
|
|
|
||||||||||
|
|
|
|
|
|
ограни чени е, при чем вели чи на |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
невязокдостаточновели ка, поэтому |
|
|
||||||||
|
|
|
|
|
|
|
|
|
строи м отсекаю щ и еплоскости : |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
£: b , -x)
8 - = 2x2 -
x8 - |
) x4 |
1 |
2 |
|
x |
|
x |
T £ 15 |
)- 62 . 2 - ; 97 . 2+ - |
||
1 |
|
|
2 |
|
|
|
x |
x |
2 |
T £ 9 +) 62- . 2 |
;- 97 . 2 |
)( |
|
1 |
|
|
|
|
|
|
Д обавляем эти ограни чени я кзадачели нейного программи ровани я и |
|
|
||||
находи м следую щ еереш ени е x2 = |
) , которое05 . 2; 52уже.(2является |
|
|
|||

|
|
|
56 |
|
|
|
|
|
|
|
|
|
|
хорош и м при бли жени ем копти - |
мальной точке. Х отя вэтой точкепо- |
|
|||||||||||
прежнему обаограни чени я наруш ены , вели чи наневязокнепревосходи т0.1, |
|
||||||||||||
поэтому положи м x* = x2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
П р имер 2. |
Реш и тьметодом секущ и х плоскостей задачу |
|
|
|
|
|
|
||||||
|
|
ϕ |
= 1 - x2 ®xmax |
|
|
|
|
|
( |
) |
|
|
|
|
|
1 |
= 12 + x22 ≤ 9x f x |
( ) |
|
|
|
|
|
|
|||
Р ешение. |
В ы берем x0 = |
),3.(В2ы чи сли м Ñ |
= |
1 |
|
x |
2 |
) . xТ 2;огдаf 2(x( |
) |
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
||
|
|
|
T |
|
x |
2 |
−13x |
11 |
+ 6 = x4 − )x3 − ; 2 ≈ f )+ |
||||
|
|
|
|
|
|
|
|
|
|
2 |
1 |
||
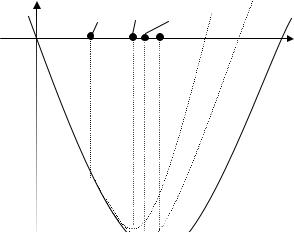
Реш и м графи чески задачу ли нейного программи ровани я
x1 − x2 → max
x |
xW £ 22 + 6 : 4 |
|
|
21 |
1 |
И з графи кави дно, что внаправлени и вектора-гради ентац елевой функц и и допусти моемножество неограни чено,
supϕ(x)
Ω1
= +¥ , т.е. ЗЛ П реш ени я неи меет.
О днако и сходная задачаразреш и ма,
x* = ( |
3 |
|
,− |
3 |
|
) .Э тотпри мер |
|||
|
|
|
|
|
|
||||
2 |
2 |
||||||||
|
|
|
|
|
|||||
и ллю стри руетсущ ественностьтребовани я ограни ченности множества Ω1.
М ето д гла дкихш тр а фо в
Д анны й метод относи тся к методам последовательной безусловной ми ни ми зац и и .
Рассмотри м задачу
f (x) → min
|
|
|
j |
≤ |
= |
|
|
; m, 1 j |
, 0 xg) ( |
|
|
||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
g x |
|
||
|
|
|
j |
|
|
|
|
, 1 + p=. +m, 0=( )m j |
|
||||
Реш ени езадачи своди тся креш ени ю |
|
последовательности задачпои ска |
|
||||||||||
безусловного ми ни мумавспомогательной функц и и |
|
|
|
||||||||||
|
|
|
F(x, r k ) = f (x) + P(x, r k ) ® min, |
|
|
|
|||||||
где P(x, r k ) |
- |
ш трафная функц и я, r k - |
параметрш трафа, задаваемы й на |
|
|||||||||
каждой |
k -й и терац и и . Н а ш трафную |
функц и ю |
наклады ваю тся следую щ и е |
|
|||||||||
ограни чени я |
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
Prkx) =( |
ì |
выполнении |
|
|
|
|
йпри, |
ограничени |
|
0, |
||
, |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
í |
|
|
|
|
|
й |
ограничени |
ии |
|||
|
|
î> 0, |
|
|
|
|
|||||||
|
|
|
|
|
|
57 |
r k → ∞, k → ∞ должно вы полняться |
||||||
2) при невы полнени и ограни чени й и |
|
||||||||||||
услови е P(x, r k ) ® ¥ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
качествеш трафны х функц и й и спользую тся, напри мер, функц и и ви да |
||||||||||||
|
k |
|
r k |
é |
m+ p |
|
2 |
m |
+ |
2 ù |
|
g |
)gx( |
|
|
) =r, Px(ê |
å |
j |
|
+ å |
j |
ú, ) x( |
|||||
|
|
|
2 |
ë j=m+1 |
|
|
j=1 |
|
û |
|
|
|
|
где |
g +j (x) = max{0, g j (x)}. |
Д анная |
функц и я |
удовлетворяет |
всем |
||||||||
требовани ям, предъ являемы м |
|
к |
ш трафны м |
функц и ям, |
и |
является |
|||||||
ди фференц и руемой. Ч то |
позволяет |
при |
безусловной |
опти ми зац и и |
|||||||||
использоватьгради ентны епроц едуры .
Алго р итм
Ш аг 1. Задать начальную |
точку |
x0, |
начальное значени е параметра |
||||||||||||||
ш трафа r 0 , чи сло C > 1 для увели чени я параметра, |
характери сти каточности |
||||||||||||||||
алгори тмаε > 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ш аг2. Положи ть k = 0. |
|
|
|
|
|
|
F(x, r k ) . |
|
|
|
|
||||||
Ш аг3. |
Состави тьвспомогательную функц и ю |
|
|
|
|
||||||||||||
Ш аг 4. И спользуя заданны енаш аге1 |
параметры |
данного алгори тма, |
|||||||||||||||
реш и ть |
задачу |
безусловной |
ми ни ми зац и и |
|
F(x,r k ) → min одни м |
и з |
|||||||||||
чи сленны х методовбезусловной ми ни ми зац и и . |
|
|
|
|
|
|
|
||||||||||
Ш аг 5. В ы чи сли ть значени е функц и и |
|
P(x* (r k ), r k ) в полученной на |
|||||||||||||||
ш аге 4 точке ми ни мума x* (r k ). |
|
|
|
|
|
|
|
|
|
|
|||||||
Ш аг 6. Е сли |
P(x* (r k ),r k )£ ε , |
то |
|
проц есс пои ска закончи ть и |
|||||||||||||
положи ть x* = x* (r k ), f (x* ) = f (x* (r k )) . |
В |
проти вном случае положи ть |
|||||||||||||||
r k +1 = Cr k |
xk +1 = x* |
r k |
k = k + 1 и перейти кш агу 3. |
, |
|
( |
), |
||||||||||
В |
данном |
методе, |
как прави ло, |
вы би раю т |
r 0 = 0; 0,01; 0,1; 1, |
а |
|||||||||||
C [4;10]. |
При |
этом |
не |
рекомендуется |
пы таться |
реш и ть |
одну |
||||||||||
вспомогательную |
задачу, |
беря |
сразу очень больш ое значени е параметра |
||||||||||||||
ш трафа |
r0 , |
поскольку |
при |
больш ом |
значени и |
данного |
параметра |
||||||||||
вспомогательная |
функц и я |
при обретает |
явно |
|
вы раженную |
овражную |
|||||||||||
структуру. |
|
|
|
x* (r k ), k = 0,1,..., |
|
|
|
|
|
|
|
||||||
Последовательность |
генери руемая |
данны м |
|||||||||||||||
методом невсегдасходи тся креш ени ю |
x* . |
Д ля частны х случаев, |
напри мер, |
||||||||||||||
когда x* |
- |
локальное еди нственное реш ени е и |
функц и и |
f (x) |
и |
g j (x) |
|||||||||||
непреры вно ди фференц и руемы в окрестности точки x* , последовательность
x* (r k ), k = 0,1,... |
сходи тся к x* . |
С ростом параметра r k генери руемы е |
алгори тмом точки |
при бли жаю тся |
к x* и звне множества допусти мы х |
реш ени й. При реш ени и задачпроц едурарасчетовзаверш ается при некотором
|
|
58 |
ш трафа r k . Полученное при этом |
конечном |
значени и |
параметра |
|
при бли женное реш ени е, |
как прави ло, |
не лежи т в множестве допусти мы х |
|
точек. |
|
|
|
Пр имер 1. Н айти ми ни мум в задаче
x2 - 4x ® min
x− 1 ≤ 0
Реш ени е. |
Запи ш ем в |
общ ем |
ви де |
(при |
прои звольном r k ) |
||
вспомогательную |
задачу для данной задачи сограни чени ями неравенствами |
||||||
|
k |
2 4x |
r k |
x[) ( |
, {Fr xx - )}}]12 . (, 0 |
=+max- |
|
|
2 |
||||||
Н айдем в общ ем ви де |
ми ни мум функц и и |
Fr kx) ( с, |
помощ ью |
||||
необходи мы х и достаточны х услови й:
ì |
r kx) ( |
dF, |
|
|
ï |
|
|
x |
|
dx |
|
|||
ï |
|
|
||
í |
r kx) ( |
dF, |
|
|
ï |
k |
|||
ï |
|
|
|
|
dx |
|
|
||
î |
|
|
||
x |
£ 0- 1 |
==2,0 - 4 |
|
|
. |
x |
> 0x- 1 x r=, 0 -)1 =(+2 - 4 |
|
|
|
|
О тсю да x* (r k ) = |
4 + r k |
|
, при чем x* |
r k |
- > 0 пр(1и )r k |
³ 0 . Полученная |
|||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 + r k |
|
услови ю |
ми ни мума, так |
как |
|||||||
точка удовлетворяет |
достаточному |
|||||||||||||||||||
2 ( * ( |
k ), r k ) r |
|
dx F |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
r k |
>=0 . + |
|
|
|
|
|
|
|
||||
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По |
полученной |
формуле |
проведем |
чи сленны е |
расчеты |
при |
|||||||||||
r k = |
|
|
|
|
; ¥ |
1000 ; |
100 |
; 10 ; 2;1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rF x |
|
|||
|
|
|
k |
|
|
|
|
r k |
|
|
|
x* (r k ) |
|
|
( * ( k ), r k ) |
|
||||
0 |
|
|
|
|
1 |
|
|
|
|
|
5/3 |
|
|
|
-3,66 |
|
|
|||
1 |
|
|
|
|
2 |
|
|
|
|
|
3/2 |
|
|
|
-3,5 |
|
|
|||
2 |
|
|
|
|
10 |
|
|
|
|
|
7/6 |
|
|
-3,166 |
|
|
||||
3 |
|
|
|
|
100 |
|
|
|
|
52/51 |
|
|
-3,019 |
|
|
|||||
4 |
|
|
|
|
1000 |
|
|
502/501 |
|
|
-3,002 |
|
|
|||||||
5 |
|
|
|
|
∞ |
|
|
|
|
1 |
|
|
|
-3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

59
При |
r k ® ¥ и меем |
lim |
|
|
4 + rk |
|
= 1 = x* . |
Е сли |
бы в этой задаче положи ть |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
2 + rk |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
r k →∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r k |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ε = 0,01, |
то |
алгори тм |
|
закончи т свою |
|
работу |
при |
|
= 1000 , |
|
так как |
|
|||||||||||||||||||||||||||||||||||||||
|
P(x* (r k ), r k )£ ε . |
|
|
В |
качестве реш ени я будет при нята недопусти мая точка |
|
|||||||||||||||||||||||||||||||||||||||||||||
* |
= ( ,00199) . |
|
|
1 |
|
|
|
|
|
x |
1000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
П р имер 2. Н айти ми ни мум в задаче |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x12 + x22 ® min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
1 + |
=x0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
|
2 − |
≤ 0 |
|
2x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Реш ени е. |
В |
|
|
данной |
задаче одно ограни чени е равенство |
|
и |
одно |
|
|
|||||||||||||||||||||||||||||||||||||||
ограни чени е |
неравенство, |
т.е. |
|
|
m = 1, p = 1. |
Состави м |
|
вспомогательную |
|
|
|||||||||||||||||||||||||||||||||||||||||
функц и ю : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
k |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
2 |
|
x |
|
|
[[ |
Fr x ] |
|
[ |
|
|
{ |
1 |
|
|
2 |
- 2)}]+ x]. |
|
|
|
x |
0(, |
+ xmax=- 1 + |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
С помощ ью |
необходи мы х |
|
|
|
|
|
|
|
|
|
|
|
услови й |
найдем |
|
безусловны й |
|
|
|||||||||||||||||||||||||||||||||
и |
достаточны х |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
ми ни мум |
|
|
Fr kx) .( |
, В ы пи ш ем |
|
|
необходи мы е |
|
услови я |
|
безусловного |
|
|
||||||||||||||||||||||||||||||||||||||
экстремума: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
¶ |
k |
|
|
ì |
|
1 |
|
|
k |
|
|
|
1 |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
), |
|
|
|
|
|
|
2(( |
|
1> )0 |
|
- 21 +x 2 |
x |
- 2 + |
|||||||||
Fr x) ( , |
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
= 0 |
= |
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
¶x |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
ï |
|
|
|
|
( |
|
|
|
|
|
), |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1£ 0 - 2 +x |
x |
|
|||||||||||||
|
|
|
|
|
î 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
¶ |
|
Fr kx) ( , |
|
ì |
|
|
2 |
|
|
|
k |
( |
|
|
|
|
|
|
|
), |
|
|
|
|
|
|
2 |
|
|
> 0 - 2 |
1 |
+x |
2 |
x + - 2 +x |
|||||||||||||
|
|
|
|
¶x |
|
|
|
= 0 = |
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
. |
|
|
x |
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
î |
|
|
, |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
+£ |
0 - 2 |
|
|
|
x |
|
||||||||||
|
|
|
|
1 + |
|
− |
|
|
> 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
При |
2 |
|
|
получи2x xм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
)r + |
|
|
k |
|
|
k |
|
2 |
|
|
|
|
( |
|
)r + |
|
k |
|
|
k |
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x* (r k ) = |
|
|
|
|
|
|
r 6 |
|
, |
|
x* |
(r k ) = |
|
r 4 |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
k |
|
2 |
|
|
|
|
|
|
k |
|
k |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
1 |
|
|
|
( |
|
) + |
|
|
|
|
|
2 |
|
|
|
|
( |
) + |
|
|
|
2 |
r 6 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+r4 |
|
|
r 6 |
|
|
|
|
|
+r4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
k |
|
|
|
* |
|
k |
|
|
|
|
|
- |
|
|
k - 8 |
2r |
|
|
|
|
|
|||||||
О днако при всех r |
|
|
|
|
и меем |
|
|
|
|
|
|
2( =( |
|
-r) |
|
x |
|
x |
|
kr |
|
|
|
|
0, |
что |
|
|
|||||||||||||||||||||||
|
³ |
0 |
|
|
1 |
|
|
|
|
|
|
2 |
|
+) |
|
) |
|
|
k |
<2 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
+ |
|
|
|
+r4 |
|
|
r 6 |
|
|
|||||||
проти воречи туслови ю |
|
1 + |
2 |
− |
|
|
> 0 дл2xя раxссматри ваемого случая. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
1 + |
|
|
− |
≤ 0 |
|
получи2x x м |
|
|
* |
|
k |
|
|
|
r k |
|
|
|
|
* |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
При |
2 |
|
|
|
x1 |
r |
|
= |
|
|
|
|
|
|
|
2 |
|
|
) = 0( .xПроведеr, м( |
) |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
+ r k |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
по этом формулам чи сленны ерасчеты .
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
r k |
|
|
|
x1* (r k ) |
|
|
|
|
|
|
x2* (r k ) |
|
|
|
|
( * ( k ), r k |
rF x |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
5/9 |
|
|
|
|
|
|
-2/3 |
|
|
|
|
||
1 |
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
3/4 |
|
|
|
|
|
|
-1 |
|
|
|
|
||
2 |
|
|
|
|
|
|
10 |
|
|
|
0 |
|
|
|
|
|
|
|
|
35/36 |
|
|
|
|
|
-5/3 |
|
|
|
|
||||
3 |
|
|
|
|
|
100 |
|
|
|
0 |
|
|
|
|
|
|
|
2600/2601 |
|
|
|
|
|
-100/51 |
|
|
|
|||||||
4 |
|
|
|
|
|
1000 |
|
|
|
0 |
|
|
|
|
251000/251001 |
|
|
|
-1000/501 |
|
|
|
||||||||||||
5 |
|
|
|
|
|
|
∞ |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
-2 |
|
|
|
|
||
|
|
|
k |
|
|
|
|
|
|
|
|
* |
|
k |
|
= |
|
|
r k |
|
|
= |
|
* |
|
|
k |
|
= 0( , |
|
|
|
|
|
При |
|
r |
|
® ¥ |
|
и меем |
|
|
x1 |
r |
|
|
|
|
|
|
|
|
2 |
|
|
|
) |
1,r |
т.еx. |
) ( |
||||||||
|
|
|
|
|
|
|
|
|
+ r k |
|
|
|
|
|
||||||||||||||||||||
последовательность точек, |
|
rk →∞ |
|
|
|
2 |
|
|
|
|
|
|
|
|
сходи тся к |
|
||||||||||||||||||
генери руемы х данны м алгори тмом, |
|
|||||||||||||||||||||||||||||||||
реш ени ю |
задачи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
З а да чи для са мо сто ятельно го р еш ения |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1. М |
етодом секущ |
и х плоскостей реш и ть следую щ и езадачи : |
|
|
|
|
|
|
||||||||||||||||||||||||||
1) |
1 - 2 |
® min |
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x1 + x2 £ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x2 |
|
|
x |
2 |
4+£ 0 - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 + 2 |
→ max |
|
x ) |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x2 |
+ x |
2 £ 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1x x,2 |
³ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 . М |
етодом ш трафны х функц и й реш и ть следую щ и езадачи : |
|
|
|
|
|
|
|||||||||||||||||||||||||||
1) |
|
1 |
|
2 |
|
x24-®x maxx 2+ |
|
2) |
|
|
|
|
|
2 |
|
1 |
|
2 3 ® maxx+ |
x-+8 |
|
4x- |
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||||||||||
|
|
- |
|
1 - |
2 = 6 ; |
x 2 3x |
|
|
|
- 1 - 2 = 2x ; |
x |
|
|
|
|
|
|
|
|
|
||||||||||||||
3) |
( |
|
1 |
|
)2 |
( |
2 |
)2 → extr+− |
4)+ |
|
4x |
1 |
-xxx ®4min |
|
|
|
|
|
ln |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 - 2 £ 2 |
x 2x |
|
|
|
|
|
- 1 £ 01 x |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 ³ , |
2 ³ 0 ;x x 0 |
|
|
|
|
2 |
|
2 |
|
+= 0 .-x4 |
|
|
x |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||
3.М |
етодами |
возможны х и подходящ и х направлени й реш и ть следую щ и е |
|
|||||||||||||||||||||||||||||||
задачи : |
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
) |
2 |
( |
|
2) |
2 |
|
|
|
|
|
|
|
|||||
1) |
|
2 |
|
|
|
|
|
2 |
|
|
|
3x |
2) |
|
|
|
|
|
→x minx − 4 |
+ |
|
|
||||||||||||
|
1 |
|
|
|
|
|
x+5 ® minx x+4 |
1 |
|
|
|
2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 + 2 ³ x4 |
|
x |
|
|
|
|
|
|
|
1 + |
2 £ 4x x2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 ³ , |
2 ³ 0 ;x x 0 |
|
|
|
|
|
|
|
1 + 2 ³ x3 |
|
x |
|
|
|
|
|
|
|
|
|
||||||||||||
3) - x1 - x2 ® min |
|
|
|
|
|
|
|
|
|
|
|
1 ³ |
, |
|
2 ³ 0 ;x x |
|
0 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
12 + |
|
22 £ 25x. |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. Реш и тьметодом ли неари зац и и : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
|
|
|
|
|
61 |
|
|
xx2+®xmin+ |
|
|
|
||
1 |
xx |
2 |
®- xmin+ |
|
3 |
2 |
1) |
|
2 |
2) |
|||||
1 |
|
|
|
|
|
|
1 2 |
2 |
|
|
|
|
|||
x + x |
2 |
£ , 804 |
5 |
|
|
|
xx += x |
,+80 |
4 |
5 |
|
||||
1 |
|
|
|
|
|
|
|
|
13 |
2 |
|
|
|
|
|
x1 +2x2 £ , 34 |
|
|
|
2 |
x4x1=+ x,2 +34 |
|
|
|
|||||||
x1, x2 ³ 0 |
|
|
|
|
|
xi ³ 0, "i |
|
|
|
|
|
|
|||
§ 7. За да ча |
кв а др а тично го |
|
пр о гр а ммир о в а ния |
|||||||||||||||
Задачей квадрати чного |
программи ровани я |
назы вается |
задача |
|||||||||||||||
вы пуклого программи ровани я |
ми ни ми зац и и квадрати чной |
функц и и |
на |
|||||||||||||||
допусти мом множествеΩ , |
|
заданном ли нейны ми ограни чени ями |
|
|
||||||||||||||
|
|
|
|
T |
|
T |
+ |
® min+ |
, |
|
|
c |
bx |
x |
Qx |
|
||
где = |
|
|
|
|
x Ω , |
|
|
|
|
|
|
|
|
|
|
|
||
ijQ) -q(си мметри чная положи тельно определенная матри ц а размера |
||||||||||||||||||
n × n , b - фи кси рованны й векторразмераn , c - заданноечи сло. |
|
|
|
|||||||||||||||
В |
данном |
параграфе рассмотри м |
|
задачу |
квадрати чного |
|||||||||||||
программи ровани я ви да |
1 n n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x) f=( |
|
å å |
|
+ å |
|
|
+ |
® min |
c |
x b |
q x |
|||||
|
|
|
|
|
|
|||||||||||||
|
|
|
2 i 1 j 1 |
j |
|
ijj=1 |
j j |
|
= = |
|
|
|
|
|
||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i å |
j |
|
ij i |
|
|
|
= |
,m1 |
£i ,b0-= a x |
( g) x |
||||
|
|
|
|
j =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x= |
|
. £j0, |
|
|
|
|
|
||||
|
|
|
|
|
j |
|
,-1n |
|
|
|
|
|
||||||
Д ля |
данной |
задачи |
условной |
опти ми зац и и |
можно |
рассмотреть |
||||||||||||
функц и ю |
Л агранжа ви да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n |
n |
n |
|
|
|||
|
|
|
|
|
j |
ij |
j |
j |
|
2 i |
|||||||
|
j |
j |
|
|
||||
При этом услови я |
К уна - |
|||||||
си стемы равенстви неравенств: |
||||||||
|
|
|
|
∂L = å |
i |
ij |
||
|
|
|
|
|
|
n |
|
|
|
|
|
|
¶x j |
i=1 |
|
|
|
m |
|
|
|
n |
x j ) = ( - xm g) +( |
|
|
|||||
å i |
i |
|
å j |
xl f ) +( |
L)x=l,( |
|||||||
i =1 |
|
|
|
j =1 |
|
|
|
|
|
|
|
|
m |
|
æ n |
|
j -ij |
ö |
+ |
|
n |
λx ( |
α +å å x |
||
|
|
ç |
i |
i ÷ |
å μ j -=+j )β+. |
|||||||
i |
|
è j |
|
|
ø |
|
|
j =1 |
|
=1 |
=1 |
|
Т аккера запи ш утся |
в ви де следую щ ей |
|
||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
å |
|
a+l |
|
+ |
|
= |
|
n,1 =j- m, 0 |
|
|
b q x |
|
i=1 |
j |
ij |
i |
j |
|
|
|
|
|
|
|
|
∂L = åα |
|
β x |
= -, m1 £0i, |
|||||||
|
|
n |
j |
ij i |
|
|
|
|
|
|
¶λi j=1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
∂L |
|
|
|
|
|
|
|
|
|
|
j |
|
x= , n1 £j0,= - |
||||||
|
|
¶μ j |
|
|||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
62 |
|
||
æ n |
ö |
|
|
|
|
|
|
|
ç |
å |
÷ |
|
a |
l= ,lm1= 0ig, |
x |
||
ç |
b - = |
i |
||||||
|
j ij i ÷ |
|
i i |
|
||||
è j =1 |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- m j |
j = |
|
|
x= |
|
|
|
|
|
|
|
|
j0, |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
,n1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
li ³ |
= |
|
|
|
m j ³ |
|
|
|
|
|
|
|
|
= |
|
|
. j , 0 |
i , ,m1 |
0, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,n1 |
||||||||||||||||||||||
По теореме К уна - Т аккера реш ени е этой си стемы |
является и скомой |
|||||||||||||||||||||||||||||||||||||||
точкой ми ни мума функц и и |
f (x) |
на множестве Ω . |
В ведя дополни тельны е |
|||||||||||||||||||||||||||||||||||||
переменны е |
|
|
|
, |
|
|
, |
полученнуюi |
|
си стему перепи ш ем в ви деси стемы |
||||||||||||||||||||||||||||||
n+i |
=x ,m1 |
|
||||||||||||||||||||||||||||||||||||||
равенств |
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
å |
|
|
j |
ijå +i aijl |
|
j |
|
|
|
|
|
|
|
j |
|
|
= |
|
n,1 |
j- =,- mb |
|
|
|
|||||||||||
|
|
|
|
|
|
i=1 |
|
n |
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å |
j |
ij + |
|
|
i |
|
n, i= |
,m1 |
b =ia |
|
+x |
x |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
j =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
³ |
|
|
= |
|
|
|
|
|
|
|
0,n |
|
|
j |
|
|
|
|
|
(1) |
|||||||||
|
|
|
|
|
|
|
|
|
|
j |
|
|
, 1 +xm |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
l |
+ii =n |
|
x = |
|
|
|
, ,i1 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0m |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
m j |
j = |
|
|
x= |
|
|
|
|
|
|
j0, |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
,n1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
λi |
³ 0 |
|
|
|
|
|
|
, m, , |
|
|
i |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
μ j ³ 0 |
|
|
|
|
, |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
=1 n, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Реш ени е |
|
|
|
|
x |
x |
xλ |
λ |
μ |
μ |
n |
) данной,..., |
|
си стемы, |
,n...+, |
m ли, |
нейны х,..., |
|||||||||||||||||||||||
|
|
|
|
|
|
+ |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
m |
1 |
|
2 n |
m |
|
|
|
|
|
||||||
уравнени й |
|
содержи т, |
по крайней мере n + m нулевы х коорди нат. |
Задачу |
||||||||||||||||||||||||||||||||||||
нахождени я |
реш ени я |
си стемы |
|
без |
|
|
|
услови й |
|
l |
+ii =n |
x = |
|
, |
,iи1 |
|||||||||||||||||||||||||
|
|
|
|
|
0m |
|||||||||||||||||||||||||||||||||||
m j j = |
x= |
|
|
можнj0, о свести кнахождени ю |
допусти мой бази сной точки |
|||||||||||||||||||||||||||||||||||
,n1 |
||||||||||||||||||||||||||||||||||||||||
методом и скусственного бази сав спец и ально построенной задачели нейного программи ровани я
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
|
+m n→ min |
1 |
n |
nz 1... |
2 |
|||||||||||
n |
|
n |
+iaijl |
|
|
|
|
|
|
|
|
|
|
|
=j |
|
|
|
j- =, |
b+- m z |
|
|||
å |
j |
ijå |
|
|
|
|
|
|
|
|
j j |
|
n,1 |
|
||||||||||
i=1 |
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å a |
j |
ij |
+ |
|
|
+ |
|
|
i |
= |
|
m,1b+i= , |
+ |
z x |
x |
|||||||||
j=1 |
|
|
|
|
|
i |
n n |
i |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
³=n,1 |
j ³ 0 x z, 0 |
|
|||||||
|
|
j |
|
j |
|
|
|
|
|
|
+ m |
|
|
|||||||||||
li ³ |
|
= |
|
|
m j ³ |
|
|
|
|
|
= |
|
. |
j , 0 |
i , ,m1 |
0, |
||||||||
|
|
|
|
|
|
|
|
,n1 |
||||||||||||||||
При реали зац и и методаи скусственного бази саследуетучи ты ватьуслови я |
|
|||||||||||||||||||||||
|
|
l |
+ii =n |
x = |
|
|
|
, ,i1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0m |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
m j |
j = |
|
|
x= |
|
, |
j0, |
|
|
|
|
|
|
|||||||||
|
|
|
|
,n1 |
|
|
|
|
|
|
||||||||||||||
т.е. невклю чатьв бази сны епеременны еодновременно λi |
и |
xn+i |
содни м и |
|||||||||||||||||||||
тем женомером i и переменны еμ j |
и x j соди наковы м номером j . |
|
||||||||||||||||||||||
П р имер 1. Реш и тьзадачу квадрати чного программи ровани я: |
|
|||||||||||||||||||||||
2 |
|
|
|
|
2 |
1 12 |
|
|
|
x2 |
® minx - x-x- 6x x+2 2 |
2 |
||||||||||||
1 |
|
|
|
|
2 |
|
|
|
||||||||||||||||
q x
( ,
z z ...
q
