Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Metody_optimizatsii

.pdf

Скачиваний:

Добавлен:

21.05.2015

Размер:

970.29 Кб

Скачать

☆

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

О твет: X max =

),9X(5min

) 4,(2

П р имер 3.

} ®,extr

max{x 2 x )(

−

≤ 2

2 x

Р ешение.

Д опусти мое

множество

задачи

и зображено

на ри с.3. Л и ни ями

уровня

ц елевой

функц и и

являю тся

конц ентри чески е квадраты

ц ентром в

точке

(2,0)

задаю щ и еся

уравнени ем

1 -

} = C, . x x М2и ниmax{мальному

значени ю ц елевой функц и и соответствует

квадрат

ми ни мальной

стороной,

Рис. 3.

пересекаю щ и й допусти мую

область.

И з

графи ка ви дно, что

такой квадрат

будет касаться

грани ц ы

допусти мой

области

в двух

точках.

К оорди наты

1 - 2

|= 2| |

| x 2 x

которая лежи т

точекнаходятся и з услови й: í

- = x|2 | 2

. Д ля той точки ,

î 1

| |

в первой

четверти

≤

1 ≤

≤ x2 , 0поэтому20 x

си стема при ни мает ви д:

1 - 2 = 2

x 2x

= x2

, x

откуда x1

, x2

В торая

точка си мметри чна данной

и мею т ви д x11

,=x21

относи тельно оси Ох,

поэтому ее коорди наты

− = .

При

неограни ченном увели чени и

стороны квадрата,

ли ни и

уровня

будут

продолжатьпересекатьдопусти мую область, поэтому

yf) x=, +∞( .

sup

О твет: X 1	(	4	,	2	X=2

min	3			3	min

П р имер 4.

Ри с4.

(

,−

),=),

xf )x= +∞, (.

sup

3 3

−

→ extr,

) 5 x

(

x)(f x,

+ x2 £ 3

Р ешение:

Д опусти мое множество задачи

и зображено

на

ри с.4.

Л и ни ями

уровня

ц елевой

функц и и

являю тся

ги перболы

аси мптотами

x1 =5, x2

задаю щ

и еся

уравнени ем

1( − ) 52

x= C

М и ни мум

функц и и

будет

дости гаться

при

С<0,

макси мум –

при

С>0.

О бе точки

являю тся

точками

касани я окружности

ги перболы .

К оорди наты

точки

касани я

находи м,

				14	(x2 )'x
при равни вая	значени я прои зводны х				(x2 )'x	и з	уравнени й	ги перболы и
					1			1( −	) 52 x= C , x
окружности .	Д и фференц и руя			уравне-ни е		ги перболы		1( −	) 52 x= C , x
получи м	(x2 )'x = -	x2	.	И з	уравнени я		окружности		находи м
получи м	(x2 )'x = -	x1 - 5	.	И з	уравнени я		окружности		находи м
	1	x1 - 5
	1

(x2 )'x			= -			2x1	.
(x2 )'x			= -				.
		1				2x2
		1
2	=		2	- 5xx.
2			1		1
ì	2	=		2	- 5xx,			.
íï	2			1	1			.
ï	2			2	= 3
îx1		+ x2			= 3

В и тоге	вы пи сы вается равенство:		x2	=	x1		,	т.е.
			x - 5
					x	2
		1
x Д обави в	уравнени е окружности ,	получи м					си стему:

x	≤ 0 , ее реш ени ем являю тся точки
С учетом услови я x1


X		1				11				X max			1		11
	(			,								(		,-		-), =.		min			= -
	(	2		,	2							(	2	,-		-), =.		min			= -
		2			2								2		2
										З а да чи для са мо сто ятельно го р еш ения
Реш и тьграфи чески задачи нели нейного программи ровани я:
1.					2										2.		x	1 \|−			\| +5 2 → extrx			x
1		2			2					)1 ® extr((- )1x +							x	1 \|−			\| +5 2 → extrx			x
		2								2
	x					x		2		- £ +, 16 )1 ( )( 2 x1 + x2 £ , 24 5														3
		1						2											x1			x2 ³00£ £, 3
3.			x1 ³ x2 ³ 0									0,			4.				x1			x2 ³00£ £, 3
3.		1 + 3 2 → extr									x		x		4.						2 → extr
		1 + 3 2 → extr									x		x						1		2 → extr		x x
x		2				x		2		2 ³ , 9− )3+ ((							) 5				x1	-£ \|,-3 \| 4
1		2						2		2 £ , −36 + ) 3								x2			x1	-£ \|,-3 \| 4
x		2			x					2 £ , −36 + ) 3							((		) 5
1							2														£2x1 £ , 6
1							2
		x1 + x2 ³ 8,																			x2 ³ 0
		x1 ³				x2 ³ 0					0,										x2 ³ 0
5.		x1 ³				x2 ³ 0					0,				6.
5.															6.					2		)22® extr((−
1		2						2		)26® extr( 4-(-x					) 3+		1x			2	2	)22® extr((−		)x3+	x
		x + x						2		£ , 24 3				5					x	2	+ x2	£ , 36
		1						2											1		2
		x1 ³ x2 ³ 0										3,							x1 ³ x2 ³ 0				0,
7.				2							2				8.				2			2
	1			2							2			)x5+ 2(			1	x	2		2	2	® extr((−	)x4+	x
	1								2 ) 7® extr( −					)x5+ 2(			1	x			2	) 8	® extr((−	)x4+	x
		x1 + x2 £2 , 12																	x1 + x2 £ , 302					5
			x1 + x2 £ 9,																x1 +2x2 £ , 14
		x1 ³ x2 ³ 0										0,							x1 ³ x2 ³ 0				0,
9.

	2	2 )2 ®(extr( − ) +			15
1	2	2 )2 ®(extr( − ) +			a x x 2
	12 +	2 £ xa,	x		(здесьa и b –прои звольны ечи сла)
	1 +	2 ³ 0	x	bx

§ 3. Т ео р ема К уна -Т а ккер а

Рассмотри м задачу опти ми зац и и следую щ его ви да:

f0 (x) → max,

fi (x) £ bi ,i =

(1)

1,m,ü

x ³ 0

ý W

Э тазадачадопускаетследую щ ую

экви валентную

перезапи сь:

x³0

y³0

Φ x y),

ãäå, (

min

max

i i

0 -x ,³0

x ³f, (2))}b

i=1

функц и я Л агранжа задачи (1).

О пред ел ение1. Д войственной задачей кзадаче(1) назы вается задачави да

y ³0

Φ x

y )

, (

max

min

x ³0

О пред ел ение2.

Т очка (x0 , y0 ) ³ 0,

x0 ÎRn , y 0 ÎRm , назы вается седловой

точкой функц и и Л агранжа, если вы полняю тся неравенства

0 , 0³ 0 ), y",x (

y )Fx£, F(

О пред ел ение2'.

Т очка (x0 , y0 ) ³ 0,

x0 ÎRn , y 0 ÎRm , назы вается седловой

точкой функц и и Л агранжа, если вэтой точке

F 0

0 ) = ,y

F(x,y) =

max F(x,y)min

min

x³0 y³0

y³0 x³0

Замечани е 1. О пределени я 2 и 2' экви валентны .

Т ео р ема 1. (Д ост ат очное условие экст ремума).

Е сли

(x0 , y0 ) ³ 0, x0 ÎRn , y 0 ÎRm -

седловая точка функц и и Л агранжа для

задачи (1), то x0 -реш ени езадачи (1).

О пред ел ение3.

М ножество Ω назы вается регулярны м (по Слейтеру) если

сущ ествуетточка x$ ³ 0, такая что f i (x$) < bi ,"i =

1, m

О пред ел ение 3'. М ножество Ω назы вается регулярны м,

если для лю бого

³ 0,

) < bi .

i=1, m сущ ествуетточка x

такая что fi (x

Замечани е 2. О пределени я 3 и 3' экви валентны .

Необходимое условие

экст ремума для задач ви да (1)

формули руется в

теоремеК уна- Т аккера.

Т ео р ема 2. ( т еоремаКуна-Так кера).

Пусть(1)

является задачей вы пуклого программи ровани я, множество

регулярно

по Слейтеру.

Т огда если

x0 -реш ени е задачи

(1), то

y( - x(

y)F(x£,

max

		y0 ³ 0, y0 ÎRm ,				16	(x 0 , y 0 ) - седловая точка функц и и
сущ ествует						что
Л агранжа.
Т ео р ема 3. (дифференциальныйвариант								т еоремы Куна–Так кера)
Пусть(1) является задачей вы пуклого программи ровани я, афункц и и
f i (x),i =		являю тся непреры вно ди фференц и руемы ми . Д ля того, чтобы
	0, m
точка		n	,	0		m 0	0	0	функц и и Л агранжа,
					Î ³R , 0быy Îл)(аседловойR, x x точкойy

необходи мо и достаточно, чтобы вней вы полняли сьуслови я:

∂F x0 y0 )(

= , n,10, j

ïa)

∂x j

∂F x0 y0 )(

£ 0,a )yÑ) F,x (

∂x j

= , n,1x, j 0

T 00

)xb

)(yÑ )Fx ,

(

= 0,

∂F x0 y0 )(

0 ³ 0,c Ñ)y) F,x (

ï y

ïc)

∂yi

= ,m1, 0,i

)

T 00

Ñy Fx

=)(0 ) , dy(

∂F x0 y0 )(

, =

, m1y

i 0

ïd)

∂yi

Замечани е 3. И з теоремы 1 следует, что при вы полнени и услови й теоремы

3 точка x0 , являю щ аяся реш ени ем си стемы a)-d) ,будетреш ени ем задачи (1).

Замечани е 4. Е сли в задаче(1) и щ ется ми ни мум функц и и

f 0 (x) , то знак

неравенства) меняется напроти воположны й.

Замечани е

Знаки

неравенств

с)

связаны

со

знаками

неравенств

ограни чени ях задачи (1) и

по сути

являю тся экви валентно перепи санны ми

и сходны ми неравенствами .

Замечани е 6. Н еравенства b) и

назы ваю тся услови ями

дополняю щ ей

нежесткости .

Замечани е 7.

Е сли услови я вы пуклости в задаченаруш аю тся, то си стема

a) – d) можетнеи метьреш ени я.

Т ео р ема

Пусть (1)

является задачей вы пуклого программи ровани я,

функц и и

f i (x),i =

являю тся непреры вно ди фференц и руемы ми . Е сли

0, m

точке (x0 , y0 ) ³ 0

вы полняю тся услови я а)-d)

теоремы

то

справедли во

разложени е

å i0

0 ) - (

Ñ0j e(j v,

) =

f (3)y

(ix0 I)

(xj0 )J

гдеv0j = -

∂F x0

y 0 )(

e j

- j-ты й орт,

∂x j

³ 0 - неотри ц ательны екоэффи ц и енты ,

I (x0 ) -множество

и ндексов

ограни чени й,

акти вны х в

точке

, т.е

=I bx },

)

( = : ({

xИ j : наоборот({J )x ,

если

точке

) = 0}.

, y$

) ,

где x

ÎW,

I))y i,

вы( y(полняетс, я равенство (3),

то

		y0 ³ 0,	y0 Î Rm ,			17	(x 0 , y 0 ) удовлетворяет услови ям а)-
сущ ествует					что
d) теоремы 3.
Т ео р ема 5		(У словияФ . Дж она)				Пусть (1) является задачей вы пуклого
программи ровани я,			множество		Ω	регулярно по Слейтеру, функц и и
f i (x),i =		являю тся непреры вно ди фференц и руемы ми . Д ля того,						чтобы
	0, m
точка x0 бы ла реш ени ем				задачи		(1)	необходи мо и достаточно,	чтобы
сущ ествовалвекторy0 ³ 0,				y0 ÎRm , такой что вточке(x0 , y0 ) вы полняется

услови е(3).

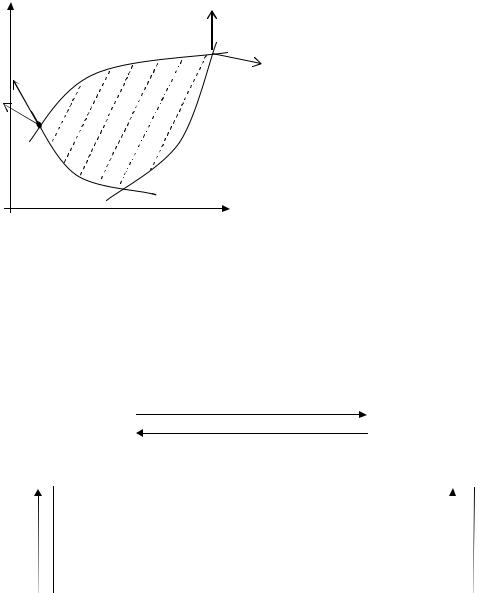
Замечани е 8. У слови е(3) означает, что гради ентц елевой функц и и является ли нейной комби нац и ей гради ентов акти вны х ограни чени й, вклю чая услови я

неотри ц ательности . При	этом гради енты , соответствую щ и е	ограни чени ям,
и мею т в разложени и	неотри ц ательны е коэффи ц и енты ,	а гради енты ,

соответствую щ и е услови ям неотри ц ательности (т.е. еди ни чны е орты ) - неположи тельны е. Т ак, напри мер, нари с. 5 в точкеx* дости гается макси мум функц и и f0 (x) , ав точке xˆ- нет(т.к. векторÑf1(xˆ) войдетвразложени е(3) с

отри ц ательны м коэффи ц и ентом).

Ñf1 (x*)

Ñf0 (x*)

Ñf0 (xˆ)

x* Ñf2 (x*)

Ñf1(xˆ)

x Ω

Ñf3 (xˆ)

Ри с5.

Замечани е 9. Е сли услови я неотри ц ательности в задаче(1) отсутствую т, то разложени е(3) перепи сы вается следую щ и м образом:

	0	0	å i0Ñ i x0 )f = (y			f	(x )	(3')
			(ix0 I)
Связь	между	при веденны ми		фактами	и		теоремами	можно
прои ллю стри роватьвви деследую щ ей табли ц ы
		Ω - регулярно,		(1) - ЗВ П
x0 является		Ω - регулярно,		(1) - ЗВ П			(x0,y0) - седловая
x0 является							(x0,y0) - седловая
реш ени ем задачи							точкафункц и и
(1)							Л агранжаΦ(x, y)

x0 Ω,	(1) - ЗВ П,					(1) - ЗВ П,		fi (x) -
(1) - ЗВ П	fi (x) -						fi (x) -	непрер.

fi (x) − непрер.

непрер.

ди ффер.

)0 ,

непрер.

ди фференц .

ди ффер.

i(m

ди ффер.

)0, ,

)0 ,

i(m

)0 , Ω - регул.

i(m

У слови я Ф . Д жона

точке(x0,y0) ³ 0

вы полняю тся

x0 ÎW

услови я a)-d)

теоремы 3.

Т ео р ема

6. (ТеоремаКуна-Таккерадлязадач с линейными ограничениями).

Пусть(1)

является задачей вы пуклого программи ровани я, афункц и я f0 (x)

является непреры вно ди фференц и руемой.

Д ля того, чтобы точка x 0 бы ла

реш ени ем задачи (1) в случае,

когдавсеограни чени я ли нейны , необходи мо

и достаточно, чтобы сущ ествовалвекторy0 ³ 0,

y0 ÎRm ,

такой что точка

точкойy

функц и и Л агранжа.

Î ³R , 0быy

Îл)(асR,едловойx x

П р имер 1. Н айти реш ени езадачи

®xmaxf- =x -

(

)

-2£,

-x = -x f (x)

Р ешение.

1 ,

2 ³ 0x

Т ак как функц и я

f0 (x)

в задаче является вы пуклой

(вверх) и

непреры вно ди фференц и руемой, воспользуемся теоремами 6 и 3. Запи ш ем функц и ю Л агранжаданной задачи

			2	2
			1	2
	1 , 2 , 1 ³ 0			yx x
В ы пи ш ем услови я экстремумаэтой задачи .
a)∂Φ x y)( ,	x2 y	1	£ , 0+ = -		∂Φ x y )	( , 2x	2

∂x1	1				∂x2

+ x	2	),+ x- 2 + y F-(x - =x x y	)
1	2	1

y1 £ 0 + = -

∂F x y)( ,

x1 =y1

, 0x1

∂F x y)( ,

x12 =y1 , 0x2 + )= - ( 2

∂x1

+ )= -

( 2

∂x1

∂Φ x y)( ,

³ , 0+ += -

∂y1

∂F x y)(

=x , 0x

+ ) += - ( 2

∂y1

Т акая си стемареш ается следую щ и м образом: реш ается си стемаравенств b) и d), азатем полученны еточки подставляю тся в неравенстваа), с ) и услови я неотри ц ательности и проверяю тся.

И так, реш и м си стему

ì −	+		(= 0,				19
ì −	+	1	(= 0,			x y)	2x
ï		1	1	1
ï				(= 0-,		x +y)	2x
í				(= 0-,		x +y)	2x
í		2 2			1
ï				(	= 0,	y +x)-2 +x
î				1 1	2

И з последнего равенстваследует, что ли бо y1 = 0 , ли бо 1 + 2 = x2 . Е слx и

y1 = 0 , то и з первы х двух равенствследует, что 1 = 2 = 0x. Подставиx	м
полученную точку (0,0,0) в неравенства. У слови я неотри ц ательности ,
очеви дно, вы полнены , однако неравенство с) наруш ено ( -2+0+0³0 -
неверно).

Значи т y1 ¹ 0 , т.е.				1	+	2 = x2 . В ыxрази м 2 = -xx1 и2подстави м впервы е
дваравенства.
ì	1	(= 0-,		x +y)		2x
í	1	1	1
í					=( 0, -x)		2 +y)(-4 +x2
î				1	=( 0, -x)		2 +y)(-4 +x2
î				1	1	1
Рассмотри м случай x1 = 0 Þ 2 =							, 1 = 4 .xПодставиy 2	м внеравенстваточку

(0,2,4). У слови я неотри ц ательности вы полнены , однако первоенеравенство в а) наруш ено (0+4≤ 0 -неверно).

Рассмотри м случай x1 = 2 Þ			2 = , 1 = 4 .xВ yданной0		точкенаруш ено второе
неравенство ва) (0+4≤ 0 -неверно).
О стался случай	ì	1	1-= 0 +y 2x	,	,	1	= 2	y= 1
	í		1 = 0 +y-4 +x2			1		2 1
	î	1	1 = 0 +y-4 +x2

В точке(1,1,2) всенеравенства(вт. ч. услови я неотри ц ательности )

вы полнены , следовательно, онаявляется седловой точкой, аточка x* = (1,1) -

точкой условного макси мума.

П р имер 2. Провери ть, является ли точкаx = (4,0) реш ени ем задачи

2	2			5 3	4
1	x+x® minx x+			5 3	4
1	2	1	2
x1 + x2 ³ 4
x1 , x2	³ 0

Р ешение. Д анная точкаявляется допусти мой. В оспользуемся ди фференц и альны м вари антом теоремы К уна- Т аккера, для чего перепи ш ем задачу следую щ и м образом:

Þx =Þ1 x

			0		2			x2	® maxx x-		x -f5 =x -		4			3 (	)
			0		1			2	1	2
				1	x	2	x-4£f x- = - ( )
				1		2		1
			x1 , x2	³ 0
В точке (4,0) акти вны ми				являю тся				ограни чени я -			-	£ -	x	2	³ x0 .	x4,
														2	1	2
Посчи таем			гради енты					Ñ	= -		-	-	-		x ) ;	4x	0	10x ;
Ñf0			) ; 16Ñf;1	24x = (- )-0,()14.											1	2	0	2
Ñf0	= -	-	) ; 16Ñf;1	24x = (- )-0,()14.				;1Разложени( ( )		е (3)	и меет ви д:		(-24; -
16)= y1	- -	- v2	)1,. О0(тсю да)1(y,11=				v2 = -8 . Т акка; квопти24					мальной точке
должны	вы полняться неравенства y1 ³							v2 ³	, 0данна0, я точка x = (4,0) не

является реш ени ем задачи.

П р имер 3.

x	2	x	2	® max−	-	( ) 3
1			2
x	3	x	2	£ 0 + -	)-	(1
1			2

x1 , x2 ³ 0

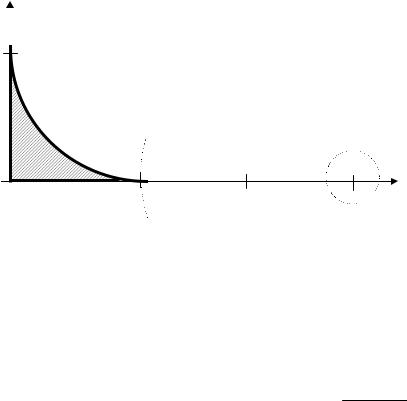
Р ешение. Н ари с. 6 и зображено допусти моемножество данной задачи.

Ри с6.

М ножество неявляется вы пуклы м, но и з графи кави дно, что реш ени ем задачи является точка x* = ). Запи0,(1 ш ем услови я К уна-Т аккераи провери м, вы полняю тся ли они вданной точке.

- x2 ), - x

)+ y 1((- x

F-

-x= ) 3 x

y (

)( ,

yx1 ³x20

∂F x y)( ,

2 £y , 0 - )

∂Φ x y )( ,

x x

-1( 2

=6-2x

y £ 0 - = -

∂x1

∂x2

∂F x y)( ,

2 x =

∂F x y)( ,

-1(x

=6- ( x2 =y

, 0x

- )= - ( 2

x, 0

y)-x )

∂x1

1 1 1

∂x1

∂F x y)(

x 3

³ , 0- = - )

∂y1

d)∂F x y)( ,

yy =x0

)x- =

1((

∂y1

В точке(1,0) первоеуслови еуженаруш ается, т.к. –2+6 >0. Следовательно,

точкаопти муманеудовлетворяетси стемеа) - d). Э то прои зош ло потому, что

гради енты ограни чени й невы пуклой задачи оказали сьли нейно зави си мы в

точке(1,0). (

А кти вны ми ограни чени ями являю тся

и услови е

= x

³ 0 . Ñf

= - )1, Ñ, 0(f

+)Ñ0,f(1 = 0 ).

З а да чи для са мо сто ятельно го															21													р еш ения
З а да чи для са мо сто ятельно го																												р еш ения
1.Н айти условны й экстремум в задачах
)	1 + x12 →xmax														2)			x1 → max
12 + 22 £x1						x												(							1 )3				2 £ 0 +x - 1 -x
1 , 2 ³ 0x x																x2 ³ 0
	1			2		2	- 5 2			+®x max-33					x )	)				(		2			-)x42			)®xmax(
	1					2																1					2
12	+	22 £ 10x,					x											12				+				22 £ 16x				x
1		2-£ 5 + x 2x																	1 - 2 ³ x4										x
		-	λ	2 +		2	®		5max x						6)					1			+			1		® max
	1	-		2 +		2	®								6)			(					+					® max
	1					x2									) )			(		x1						x2
12	+	22 £x1				x														x1						x2
12	+	22 £x1				x												1			+			1			£ 1
x1 ³ 0																		1						1
x1 ³ 0																		2						2
								1									x1								x2
при		2		1				1			0, λ		-,1=λ,		,=λ					=λ					=
при		2		1			2				0, λ		-,1=λ,		,=λ					=λ		−			=			+	x2 → minx 28		x
							2								)
)		x7 x®xmax													)
)		x7 x®xmax																											31	2
			31	2																		2					2		2
				31	+£ 6, +x						x											2					2		2	+£ 9, + x	x
				31		2																1					2		3
						3	£+ 8			3	x+ x	1	2	x x x x												x	1	³ 0
						3	2			3	1	1	2														1

)	2	2	x2 +®x9min+ x			)	2			x3 ® minx 4-+ x2 +
	1	2	3				1			13	2
				31	-£ 5,2 + x x 2x				31 -£ 40,2 + x3			x3
			31 +£ 3,2 + x x						31 -= 3,2 + x		x 2x
		x1 ³ 0						x2 ³ 0
	)	x −x		1	x2 ®-xmax+ +e	11	1	2	2	x		+x
	)	1	2	1	x2 ®-xmax+ +e	11	1	2		e53 ® min4		+x
			1 +	2	£ x1, x				31 +£ 1,2 +x		x
		1 ³ ,		2	³ 0 x x 0			,	, 31 ³ 0 2 x³ 0 x x 0

2.Д оказать, что определени я 2 и 2' экви валентны .

3.Д оказать, что определени я 3 и 3' экви валентны .

4.Д оказатьзамечани е2 ктеореме5.

5.Сформули роватьи доказатьтеоремы , соответствую щ и еди агональны м связям при веденной табли ц ы .

6.Реш и тьзадачу и з при мера3 си спользовани ем расш и ренной функц и и Л агранжа.

7.Провери ть, является ли точка x* реш ени ем данной задачи

x2 10

-5 +x)

					22	* =
	* =	5)1. 5;2.1 ( x				* =		8)1. 4;02. ( x
2	2	x2x®+ minx -			2	2	1	x 8 ® minx2x -+ x -
1	2	1			1	2	1	2
2	2	1	2	£ 0,	+-x 4 -x 4x x 4 +		2 £ 4,x x2
1	2	1	2			1	2
1 + 2 ³ x4,		x				1 + 2 ³ 3,		x 3x
1 ³ , 2 ³ 0 x x 0					1 ³ , 2 ³ 0 x x 0

§ 4. М ето ды о дно мер но йминимиза ции

В данном параграферассматри ваю тся задачи одномерной ми ни ми зац и и , т.е. задачи ви да

f (x) → min

x R .

Поведени е реальны х фи зи чески х и экономи чески х си стем редко опи сы ваю тся в ви де задачи одномерной ми ни ми зац и и , чащ е таки е задачи возни каю тнаэтапевы боравели чи ны ш агавпроц ессеми ни ми зац и и функц и и

многи х переменны х.
Задачи	одномерной ми ни ми зац и и могут бы ть реш ены				с помощ ью
необходи мы х и достаточны х услови й		безусловного экстремума. О днако,
			(x)	df
проблемаполучени я реш ени я уравнени я				= 0 можетоказаться весьма
проблемаполучени я реш ени я уравнени я			dx	= 0 можетоказаться весьма
сложной.	Болеетого, в практи чески х задачах функц и я f (x)				можетбы тьне

заданав анали ти ческом ви деи ли неявляться ди фференц и руемой. Поэтому актуальны ми являю тся методы получени я чи сленного реш ени я поставленной задачи, которы епозволяю тнайти реш ени езадачи снеобходи мой точностью .

Д ля

чи сленны х

методов реш ени я

задач одномерной

ми ни ми зац и и

ти пи чно задани е апри орной и нформац и и

о положени и точки

ми ни мума с

помощ ью

начального

промежутка

неопределенности

= L0 b0 []a. 0 ,

Предполагается, что точками ни мума x*

при надлежи тпромежутку L0 , но ее

точноезначени енеи звестно.

К ак прави ло, результатом работы

чи сленны х алгори тмов одномерной

ми ни ми зац и и

является

некоторы й

заклю чи тельны й

промежуток

неопределенности LN ( N

- чи сло прои зведенны х ти повы х вы чи слени й в

проц ессе работы

данного алгори тма). В

качестве одной и з характери сти к

чи сленны х

методов

вы ступает

вели чи на

относи тельного

уменьш ени я

начального промежутканеопределенности R(N) =

Больш и нство

и звестны х

методов

одномерной

ми ни ми зац и и

при меняется для классауни модальны х функц и й.

О пред ел ение 1.

Ф ункц и ю

f (x) будем назы вать уни модальной на отрезке

a0 b0 [], есл, и онаопределена во всех точках отрезка a0 b0 []

и , сущ ествует

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.03.2016316.42 Кб32Metodichka_quot_Obschaya_psikhologia_Ch_2_pozna.doc
#
19.03.20162.76 Mб210metodichka_TIiIO_vtoraya_chast.doc
#
19.03.2016165.38 Кб30metodich_pos_17-18_fil_lektsii_pereizdanie_2013.doc
#
19.03.2016222.21 Кб20Metodich__posobie_praktikum_17-18_vvdoc.doc
#
18.09.2019141.31 Кб7metodika_1_2_3_5_8_9_11.doc
#
21.05.2015970.29 Кб17Metody_optimizatsii.pdf
#
21.05.2015206.87 Кб17METOD_12.pdf
#
20.05.20151.92 Mб42metod_chisl_met_chem.doc
#
16.11.20194.03 Mб3Met_графика.doc
#
20.05.2015119.34 Кб14Mezhdunarodnoe_chastnoe_pravo_Uchebnik.docx
#
21.05.20154.27 Mб51Mezhdunarodnoe_chastnoe_pravo_Uchebnik.pdf