
Metody_optimizatsii
.pdf63
x1 + x2 £ 2
|
|
|
|
- x1 + 2x2 £ 2 |
|
|
||
|
|
|
|
x1 ³ x2 ³ 0 . |
0, |
|
||
Реш ени е. |
Ц елевая |
функц и я |
данной |
задачи |
является квадрати чной с |
|||
матри ц ей |
æ |
1 |
− 1ö |
Т ак как определи тели |
главны х ми норов данной |
|||
A = ç |
|
÷. |
||||||
|
ç |
-1 |
÷ |
|
|
|
|
|
|
è |
2 ø |
|
|
|
|
|
|
матри ц ы |
D1 = |
D2 =1 |
положи1, |
тельны , |
то |
данная матри ц а является |
||
положи тельно определенной, а ц елевая функц и я вы пуклой. |
Следовательно, |
|
||||||||||||||||||||
данная задача является задачей |
вы пуклого |
программи ровани я и |
|
для |
ее |
|
||||||||||||||||
реш ени я можно |
при мени ть опи санны й |
вы ш е метод |
реш ени я. |
Си стема |
|
|||||||||||||||||
равенств(1) запи ш ется для рассматри ваемой задачи вви де |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x - x + l - l - m1 = 2 2 |
11 |
|
|
2 |
2 |
|
|
2 |
|
|
||||||||||
|
- x + x + l + l - m2 = 6 2 |
|
|
11 |
|
22 |
|
2 |
|
4 |
|
|||||||||||
|
|
|
+ |
+ x31 |
= 2x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
+ 2 +xx |
= 2x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x lx lx m m |
2 |
³ 0 |
2 |
, |
1 |
, |
4 |
, |
13 |
, |
2 |
,, |
, |
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
m = m |
|
= l |
= l x4 =2 0. x3 1 |
|
x2 2 1 1 |
|
|
|
|||||||||||||
Н айдем допусти мое бази сное реш ени е этой |
|
си стемы , |
путем |
реш ени я |
|
|||||||||||||||||
вспомогательной |
задачи |
ли нейного программи ровани я |
с и скусственны ми |
|
||||||||||||||||||
переменны ми |
|
- x5 - x6 ® max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
- |
+ l - l - m + x5 = 21 |
|
|
2 x11 |
|
x2 |
2 |
|
2 |
|||||||||||
|
- |
+ |
+ l + l - m + x6 = 62 |
|
|
2 |
x11 |
|
|
2x2 |
2 |
4 |
||||||||||
++ x31 = 2x2
- + 2 +xx |
= 2x |
2 |
1 4 |
|
|
|
|
|
|
|
x lx lx m m |
2 |
³ 0 , |
2 |
, |
1 |
, |
4 |
, |
13 |
, |
2 |
,, , |
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
взяв |
в |
качестве |
первоначального |
бази сного |
множества |
|
J = { |
4,},3.56, |
||||||||||||||
При ведем последовательностьси мплексны х табли ц . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cB |
J |
|
xB |
x1 |
x2 |
x3 |
x4 |
|
|
l1 |
|
l2 |
|
|
m1 |
|
|
|
m2 |
|||
-1 |
5 |
|
2 |
2 |
-2 |
0 |
0 |
|
|
1 |
|
-1 |
|
|
|
-1 |
|
|
|
0 |
|
|
-1 |
6 |
|
6 |
-2 |
4 |
0 |
0 |
|
|
1 |
|
2 |
|
|
|
|
0 |
|
|
|
-1 |
|
0 |
3 |
|
2 |
1 |
1 |
1 |
0 |
|
|
0 |
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|
0 |
4 |
|
2 |
-1 |
2 |
0 |
1 |
|
|
0 |
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
-8 |
0 |
-2 |
0 |
0 |
|
|
-2 |
|
-1 |
|
|
|
1 |
|
|
|
1 |
|
|
-1 |
5 |
|
4 |
1 |
0 |
0 |
1 |
|
|
1 |
|
-1 |
|
|
|
-1 |
|
|
|
0 |
|
|
-1 |
6 |
|
2 |
0 |
0 |
0 |
-2 |
|
|
1 |
|
2 |
|
|
|
|
0 |
|
|
|
1 |
|
0 |
3 |
|
1 |
3/2 |
0 |
1 |
-1/2 |
|
|
0 |
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|
0 |
2 |
|
1 |
-1/2 |
1 |
0 |
1/2 |
|
|
0 |
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|

64
|
|
|
-6 |
|
-1 |
0 |
0 |
|
1 |
|
|
|
-2 |
|
|
|
|
-1 |
|
1 |
|
1 |
|
|||
-1 |
|
5 |
10/3 |
|
0 |
0 |
-2/3 |
|
4/3 |
|
|
1 |
|
|
|
|
-1 |
|
-1 |
|
0 |
|
||||
-1 |
|
6 |
2 |
|
0 |
0 |
0 |
|
-2 |
|
|
|
1 |
|
|
|
|
2 |
|
0 |
|
-1 |
|
|||
0 |
|
1 |
2/3 |
|
1 |
0 |
2/3 |
|
-1/3 |
|
|
0 |
|
|
|
|
0 |
|
0 |
|
0 |
|
||||
0 |
|
2 |
4/3 |
|
0 |
1 |
1/3 |
|
1/3 |
|
|
0 |
|
|
|
|
0 |
|
0 |
|
0 |
|
||||
|
|
|
-16/3 |
|
0 |
0 |
2/3 |
|
2/3 |
|
|
-2 |
|
|
|
|
-1 |
|
1 |
|
1 |
|
||||
-1 |
|
5 |
4/3 |
|
0 |
0 |
-2/3 |
|
10/3 |
|
|
0 |
|
|
|
|
-3 |
|
-1 |
|
1 |
|
||||
0 |
|
λ1 |
2 |
|
0 |
0 |
0 |
|
-2 |
|
|
|
1 |
|
|
|
|
2 |
|
0 |
|
-1 |
|
|||
0 |
|
1 |
2/3 |
|
1 |
0 |
2/3 |
|
-1/3 |
|
|
0 |
|
|
|
|
0 |
|
0 |
|
0 |
|
||||
0 |
|
2 |
4/3 |
|
0 |
1 |
1/3 |
|
1/3 |
|
|
0 |
|
|
|
|
0 |
|
0 |
|
0 |
|
||||
|
|
|
-4/3 |
|
|
0 |
|
0 |
2/3 |
|
-10/3 |
|
|
0 |
|
|
|
|
3 |
|
|
1 |
|
-1 |
|
|
0 |
|
4 |
4/10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
λ1 |
28/10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
4/5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2 |
6/5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
0 |
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
0 |
|
0 |
|
|||
|
В |
последней си мплексной табли ц емы получи ли допусти моебази сное |
||||||||||||||||||||||||
реш ени е |
|
|
|
|
|
|
|
|
|
4 |
|
6 |
2 |
14 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
ö |
|
|
|
|
||||||
|
|
|
( |
|
|
x |
|
x x |
, |
|
,) = ç, |
m,, |
|
ml,,,0l, |
|
|
|
0, |
÷0,.,0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
1è |
5 |
2 |
5 |
13 54 |
51 |
2 |
|
ø |
|
|
|
|
|||
Поэтому и скомое реш ени е задачи квадрати чного программи ровани я и меет
æ |
4 |
|
6 |
ö |
|
36 |
|
ви д x* = ç |
|
, |
|
÷ со значени ем ц елевой функц и и |
* =f (x*f) = |
|
. |
|
5 |
5 |
|||||
è 5 |
|
ø |
|
|
|||
За да чи для са мо сто ятельно го р еш ения
1.Реш и тьзадачи квадрати чного программи ровани я:
1) (x |
|
)2 (x |
2 |
)2 ® min4− |
+ 2 |
x1 + x2 £ 2 |
|
|||||
1 |
|
|
|
|
|
|
|
x1 ³ x2 ³ 0 |
0, |
|||
x + x |
2 |
£ 3 |
|
|
|
|
||||||
1 |
|
|
|
|
|
|
|
|
- x2 ® max |
|
||
x |
+ 2x |
2 |
£ 4 |
|
|
|
3) |
x |
20 |
|||
1 |
|
|
|
|
|
|
|
1 |
2 |
|
||
x1 ³ x2 ³ 0 |
0, |
|
|
x1 - x2 ³ 0 |
|
|||||||
2) |
|
|
|
|
xx2 |
®+ maxx - |
|
2 3 |
- x1 + 2x2 £ 2 |
|
||
x + 4x |
|
£ 4 |
21 |
2 |
|
|
x1 ³ x2 ³ 0 |
0, |
||||
2 |
|
|
|
|
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
||
§ 8. К ла ссическо е в а р иа цио нно е исчисление |
||||||||||||
|
1 |
|
П р о стейш а я за да ча в а р иа цио нно го исчисления |
|
||||||||
Пусть |
Ct1 []t- пространство, |
непреры вно ди фференц и руемы х наотрезке |
||||||||||
0 |
||||||||||||
t0 t1 [] функц, |
и й снормой |
|
|
|
|
|
||||||
63
|
|
|
|
|
1 = |
|
|
& t |
x|}.) (t |x|, |
) ( |
|
max{|t |
max |
|
|
|
|
|
|
0 ≤ ≤t t1 t |
|
|
|
|
|
|
|
|
|
Раздел опти ми зац и и , связанны й снахождени ем наи больш и х и наи меньш и х |
|
|||||||||||||
значени й |
функц и оналов, |
определенны х |
на |
1 |
0 Ct1 |
[]t, , |
назы вается |
|
||||||
|
|
|||||||||||||
вари ац и онны м |
|
и счи слени ем. В |
отли чи е от |
рассмотренны х |
ранее |
|
||||||||
экстремальны х |
задач, определенны х в конечномерном пространстве R n , |
|
||||||||||||
задача |
вари ац и онного |
и счи слени я |
стави тся |
в |
бесконечномерном |
|
||||||||
пространствефункц и й. |
|
|
|
|
|
|
|
|
|
|
||||
О пред ел ение |
1. |
|
Простейш ей |
задачей |
класси ческого |
вари ац и онного |
|
|||||||
и счи слени я назы вается следую щ ая экстремальная задачав |
1 |
Ct1 []t: |
, |
|
||||||||||
0 |
|
|||||||||||||
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ò |
|
& )) |
(®),extr( , |
( |
dt ))×( t(=x |
t x t F |
J x |
||
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
= |
|
= x1 , |
t 10x) (x0, x (t ) |
|
|
|
|
|||
|
& |
непреры вная функц и я трёх переменны х, |
ди фференц и руемая |
|
||||||||||
гдеF(t ,x, x ) - |
|
|||||||||||||
по двум свои м последни м аргументам. |
Э кстремум в задаче и щ ется среди |
|
||||||||||||
функц и й |
Î |
1 |
0 t1 ]t, |
удовлетворяю, C[x t ( ) |
щ и х краевы м услови ям |
0 |
= x0 , x (t |
) |
||||||
( 1 ) = x1 . xТ tаки ефункц и и назы ваю тся допусти мы ми .
О пред ел ение 2. Д опусти мая функц и я xˆ(×) назы вается слабы м локальны м ми ни мумом (макси мумом) задачи (1), если сущ ествует δ > 0 такое, что для
лю бой другой допусти мой |
функц и и x(×) , для |
которой x ×) (- xˆ|| × ||(1 )< δ , |
вы полняется неравенство |
× ³ (xˆ(×J)) ))( J( x × |
£ (xˆ(×J))))).( J( x |
Замечани е 1. И наче говоря, простейш ая задачавари ац и онного и счи слени я состои тв оты скани и слабого экстремумафункц и оналави да(1) намножестве всех гладки х кри вы х, соеди няю щ и х двезаданны еточки .
Н аряду со слабы м экстремумом в класси ческом вари ац и онном и счи слени и
тради ц и онно рассматри вается си льны й |
экстремум. |
При |
этом расш и ряется |
|||||||||
класс функц и й, |
среди |
которы х |
и щ ется |
реш ени е задачи. |
В ведем в |
|||||||
рассмотрени е пространство кусочно-непреры вны х |
функц и й |
|
1 |
|||||||||
|
0 t1 []t с, KC |
|||||||||||
нормой |
0 = |
t |
x| ). ( |
| |
maxx t |
|| |
) ( |
|| |
|
|
|
|
|
|
0 ≤ ≤t t1 t |
|
|
1 |
|
|
|
|
|
|
|
О пред ел ение 3. |
Ф ункц и я |
xˆ(×) Î |
|
|
|
|
щ ая краевы м |
|||||
|
0 t1 [],t ,удовлетворяюKC |
|||||||||||
услови ям |
0 |
= x0 , x (t , )( 1 ) = x1 , x tназы вается |
си льны м |
локальны м |
||||||||
ми ни мумом (макси мумом) задачи (1), если сущ ествует δ > 0 такое, что для |
||||||||||||
лю бой другой допусти мой функц и и |
x(×) , |
для |
которой |
x ×) (- xˆ|| × ||( )< δ , |
||||||||
|
|
|
|
|
(xˆ(×J)) ))( J( x × |
|
|
|
|
0 |
||
вы полняется неравенство |
× |
³ |
£ |
(xˆ(×J))))).( J( x |
||||||||
Замечани е 2. Поми мо поняти й си льного и слабого локального экстремума стандартны м образом вводи тся поняти еглобального экстремумазадачи (1), то естьфункц и и , доставляю щ ей ми ни мальное(и ли макси мальное) значени е функц и оналу J (x(×)) среди всех допусти мы х функц и й.
|
|
|
|
|
|
64 |
|
Т ео р ема . (Необходимое условие экст ремума). |
|
||||||
Е сли функц и я xˆ(×) |
доставляетслабы й локальны й экстремум в задаче(1), то |
||||||
для этой функц и и |
∂F |
|
1 |
Ct ][tи, |
вы полнено уравнени еЭ йлера: |
|
|
& |
|
|
|||||
|
|
|
0 |
1 |
|
|
|
|
∂x |
|
d ∂F |
∂F |
|
||
|
|
|
|
|
|||
|
|
|
|
|
& = |
∂x |
(2) |
|
|
|
|
dt |
|||
|
|
|
|
∂x |
|
||
Замечани е 3. Е сли |
xˆ(×) |
доставляет си льны й локальны й экстремум в |
|||||
задаче(1), то и з определени я следует, что онадоставляети слабы й. Поэтому |
|||||||
необходи мое услови е слабого экстремума является также необходи мы м |
|||||||
услови ем си льного экстремума. |
|
|
|
|
|
|
|
|
|
||||||||||
О пред ел ение 4. |
Реш ени я |
уравнени я Э йлера, |
являю щ и еся |
допусти мы ми |
|||||||||||||||
функц и ями , назы ваю тся допусти мы ми экстремалями задачи (1). |
|
|
|||||||||||||||||
А лго р итм р еш ения пр о стейш ейза да чи в а р иа цио нно го исчисления |
|
||||||||||||||||||
1. |
Запи сатьнеобходи моеуслови еэкстремума– уравнени еЭ йлера: |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
d ∂F |
= ∂F |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
dt |
|
∂x |
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
1 C2 )xCt. , |
|
|
|
||
2. |
Н айти общ еереш ени еуравнени я Э йлера |
( , |
|
|
|||||||||||||||
3. |
Н айти |
допусти мы е экстремали , |
т.е. |
реш ени я |
уравнени я |
Э йлера, |
|||||||||||||
|
удовлетворяю щ и езаданны м краевы м услови ям |
0 |
= x0 , x (t( 1) = x1 . x t |
||||||||||||||||
4. |
Д оказать, что реш ени ем является однаи з допусти мы х экстремалей, и ли |
||||||||||||||||||
|
показать, чтореш ени я нет. |
|
|
|
|
|
|
|
|
|
|||||||||
П р имер 1. |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
ò & |
|
|
|
|
|
|
= 1. |
1)x=( 0, |
0)x( |
® inf;×dt = x |
||||
1. |
У равнени еЭ йлера: |
|
dt |
0 |
= 0;2иxли 2x = 0. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
d |
& |
|
|
|
|
&& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
О бщ ее реш ени е: |
= |
1 + C2x.t |
C |
|
|
|
|
|
|
|
|
|||||||
3. |
= |
2 = |
|
|
= |
1 = 1. Т акиC |
м1)xобразом( 0; ,Cиxме(0)ется |
еди нственная |
|||||||||||
|
допусти мая экстремаль ˆ( ) = t .x t |
|
|
|
|
|
|
|
|
||||||||||
4. |
Покажем, |
что |
эта экстремаль доставляет глобальны й ми ни мум |
в |
|||||||||||||||
|
данной задаче. |
Д ействи тельно, |
возьмем прои звольную |
допусти мую |
в |
||||||||||||||
|
этой |
|
задаче |
|
|
функц и ю |
x(t) . |
|
В |
таком |
случае |
||||||||
|
|
1 |
|
|
Î |
|
= 1. |
1)x=( 0, |
0)x( 1],0 ,C[x t ( ) |
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
О бозначи м |
= |
|
) -( ˆ(t).xТ огдаt x h(0t ) = h(1) = 0 . |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 |
)2 |
1 |
|
1 |
1 |
&2 dt = h& |
+ dt+ h 2 + dt = |
|||||
|
|
|
( ˆ ))( ( |
|
( |
)) ( &( ) |
ò |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ò |
ò |
ò |
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ˆ |
|
ò &2 |
|
|
(xˆ(×J)) Следовательнdt³ (h=)) +J ×оx, |
функц и я |
ˆ( ) = t xявляетсt я |
|||||||||||
0
глобальны м ми ни мумом.

|
|
|
|
|
|
|
|
|
|
|
|
|
65 |
|
|
|
|
|
Замечани е 4. А налоги чны м образом можно сформули ровать алгори тм |
|
|||||||||||||||||
реш ени я |
|
простейш ей |
|
векторной задачи |
класси ческого вари ац и онного |
|
||||||||||||
и счи слени я. |
Пусть |
|
в |
задаче |
(1) |
× |
= |
1 × xn ×)), (x |
),... ( |
|||||||||
= |
|
|
|
|
& |
|
x |
|
) - xфункц,..x, иxFя, t 2Fn ,+..,1 переменны( , |
х. |
Н еобходи мы е |
|
||||||
|
|
|
|
|
|
& |
n |
1 1 |
n |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
услови я в простейш ей векторной задаче состоят и з си стемы |
уравнени й |
|
||||||||||||||||
|
d ∂F |
|
∂F |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Э йлера |
|
|
|
|
|
i, n .1 |
|
|
|
|
|
|
||||||
|
|
|
= |
|
|
, |
= |
|
|
|
|
|
|
|
||||
|
& |
|
¶xi |
|
|
|
|
|
|
|||||||||
|
dt ¶xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ча стны е случа и ур а в нения Э йлер а
Если функц и я F(t ,x, x& ) незави си тявно отодной и з свои х переменны х, то уравнени еЭ йлерадопускаетпони жени епорядка, то естьсводи тся кболее простому уравнени ю .
I. Е сли функц и я F(t ,x, x& ) незави си тявно отx, то уравнени еЭ йлерасводи тся куравнени ю :
|
|
|
|
|
|
∂F |
= const |
(3) |
|
|
|
|
& |
||||
|
|
|
1 |
|
|
¶x |
|
|
П р имер 2. |
|
|
2 & 2 |
|
|
= 1. 1)x=( 0, 0)x( ® inf;dt× =x t |
||
|
& |
ò |
|
|
||||
|
|
|
0 |
|
|
|
|
|
Поды нтегральная функц и я незави си тявно отx, поэтому уравнени еЭ йлера |
||||||||
и меетви д: 2t |
2 |
& |
|
|
|
|
|
|
|
x = C . |
C1 |
|
|
|
|
|
|
1. О бщ ее реш ени е: x = |
|
+ C2 . |
|
|
||||
t |
|
|
x(0) = 0 , несущ ествует |
|||||
|
|
|
|
|
|
|
||
2. Э кстремали , удовлетворяю щ ей краевому услови ю |
||||||||
3.Д анная задачанеи меетреш ени я.
II.Е сли функц и я F(t ,x, x& ) незави си тявно отt, то уравнени еЭ йлераможно перепи сатьвви де
|
|
& |
|
∂F |
- |
|
& |
) =,(const, |
x Fx t |
(4) |
|
|
|
& |
|
||||||||
|
|
x |
|
|
|||||||
|
|
|
|
¶x |
|
|
|
|
|
|
|
|
|
|
3π / 2 |
|
|
|
|
3π |
|
||
П р имер 3. |
& |
ò |
&2 |
2 |
|
|
|
= 0. ) x=( 0, 0)x( ® inf;dt- |
|||
|
|
|
|
2 |
|||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
1. |
Поды нтегральная функц и я не зави си т явно от t, поэтому уравнени е |
||||||||||
|
Э йлераможно запи сатьвви де: |
|
x × 2x - &x& 2 +& x 2 |
= C , |
и ли x&2 = C - x2 . |
||||||
2. |
О бщ ее реш ени е: |
= |
1 |
+ C2 )t . x C sin( |
|
|
|
||||
3.Е ди нственная допусти мая экстремаль xˆ= 0 .
4.Покажем, что этаэкстремальнедоставляет ми ни мумав данной задаче.
Рассмотри м последовательность функц и й |
x |
n |
t |
= |
1 |
sin |
2t |
. ( О) чеви дно, |
||||||||||
n |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||||
что xn − допусти мы ефункц и и и |
n → ˆx≡ 0 вxC1 0 3π 2], [ н,о при этом |
|||||||||||||||||
n |
1 |
|
3π |
4 |
|
5π |
|
(xˆ(×J)). |
0 = |
< |
) |
-1=( - |
())× (J= x |
|||||
n2 |
4 |
n2 12 |
||||||||||||||||
9 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
И з этого при мера ви дно, |
что уравнени е Э йлера – |
необходи мое, |
но не |
|||||||||||||||
достаточноеуслови еэкстремума. |
|
|
|
|
|
|
|
|
|
|
||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
66 |
|
|
|
|
|
|
|
|
|
||
О пред ел ение 5. |
|
|
|
|
|
З а да ча Б о льца |
|
|
|
|
|
|
||||||||||||||||
|
Задачей |
Больц а |
назы вается следую щ ая экстремальная |
|||||||||||||||||||||||||
задачабез ограни чени й в |
|
1 |
0 |
Ct1 |
[]t |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
))®( extr), |
|
( |
t+x)) t( x),f ( ,dt( × |
|||
|
|
|
|
ò |
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
0 |
1 |
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
|||||
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где ( |
0 |
t1)x)-((ft функц),x |
и я, ди фференц и руемая по каждой и з двух свои х |
|||||||||||||||||||||||||
переменны х. |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
О пред ел ение 6. |
Ф ункц и я |
|
xˆ(×) Î |
0 |
Ct []t назы, |
вается слабы м локальны м |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
ми ни мумом (макси мумом) задачи (5), если сущ ествует δ > 0 такое, |
что для |
|||||||||||||||||||||||||||
лю бой |
другой |
функц и и |
|
x(×) Î |
1 |
|
0 |
|
Ct []t ,для |
которой |
x ×) (- xˆ|| × ||( )< δ , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
вы полняется неравенство |
|
|
× |
³ |
|
|
|
(xˆ(×))B( ))( B x × |
£ (xˆ(×))B))).(B( x |
|
||||||||||||||||||
Т ео р ема . (Необходимые условияэкст ремума). |
|
|
|
|
|
|
||||||||||||||||||||||
Е сли функц и я xˆ(×) |
|
доставляетслабы й локальны й экстремум в задаче(5), то |
||||||||||||||||||||||||||
для этой функц и и |
|
∂F |
Î |
1 |
|
Ct ][tи, |
вы полнены : |
|
|
|
|
|
|
|||||||||||||||
& |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
¶x |
|
|
|
d ∂F |
|
|
∂F |
|
|
|
|
|
|
|
|
||||||||
|
a) уравнени еЭ йлера: |
|
= |
|
; |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
& |
|
|
¶x |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
dt ¶x |
|
|
|
|
|
|
|
|
|
|
||||||||
|
b) услови я трансверсальности : |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
∂F |
|
|
|
∂f |
|
|
|
|
∂F |
|
|
∂f |
|
|
|
|
|||||||
|
|
|
|
|
& (t0 ) |
= |
|
|
|
|
|
|
|
|
|
|
|
&; t1 ) =(- |
|
|
. |
|
|
(6) |
||||
|
|
|
|
|
¶x(t0 ) |
|
|
|
¶x(t1 ) |
|
|
|||||||||||||||||
О пред ел ение 7. |
|
|
¶x |
|
|
|
¶x |
|
|
|
|
|
|
|||||||||||||||
Реш ени я уравнени я Э йлера, удовлетворяю щ и е услови ям |
||||||||||||||||||||||||||||
трансверсальности , назы ваю тдопусти мы ми экстремалями задачи (5). |
|
|||||||||||||||||||||||||||
Алго р итм р еш ения за да чи Б о льца
1.Запи сатьнеобходи мы е услови я экстремума:
a)уравнени еЭ йлера: dtd ∂¶Fx& = ∂¶Fx
b) услови я трансверсальности : |
∂F |
(t0 ) = |
∂f |
∂F |
t1 ) =(− |
∂f |
|
|
& |
|
&; |
|
. |
||||
∂x(t0 ) |
∂x(t1 ) |
|||||||
|
∂x |
|
∂x |
|
|
|||
2. Н айти общ еереш ени еуравнени я Э йлера |
1 C2 )xCt. , |
( , |
|
|
||||
3.Среди всех реш ени й уравнени я вы брать те, которы е удовлетворяю т услови ям трансверсальности .
4.Д оказать, что реш ени ем является однаи з допусти мы х экстремалей, и ли
показать, чтореш ени я нет.
|
|
1 |
|
|
|
|
П р имер 4. |
& |
ò & 2 |
2 ® extr .+ |
1-) x( × =dt )x |
x ( |
))1) x( B( |
|
|
0 |
|
|
|
|

67
1. Поды нтегральная функц и я не зави си т явно от t, поэтому уравнени е
Э йлераможно запи сатьвви де: |
&& |
2 |
& |
& 2 |
+ =x C;.x |
x × 2x - x |
|
+ x = C , и ли |
|
У слови я трансверсальности вданной задачеи мею тви д:
|
ì |
2 |
= |
3 |
0) (x 4 0) (x (08)x |
|
|
|
|
|
|
|
|
|
|||||||
|
ï & |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
í |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï & |
) =( 8( ) 3 x 38x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. |
О бщ ее реш ени е: x |
|
t 2 |
1 |
+ CC2 .t+ |
= - |
|
|
|
|
|
|
|
|
|||||||
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Е ди нственная |
|
экстремаль, |
удовлетворяю щ ая |
|
|
услови ям |
|
|||||||||||||
|
трансверсальности : |
xˆ(t) |
t 2 |
3 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
+ |
= - |
|
|
|
|
|
|
|
|
|
|||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||
4. |
Покажем, |
что |
эта экстремаль доставляет глобальны й |
ми ни мум |
в |
|
|||||||||||||||
|
данной |
задаче. |
Д ействи тельно, |
возьмем |
прои звольную |
функц и ю |
|
||||||||||||||
|
Î |
1 |
1]0и, сравни[Ch (t )м значени я |
( ˆ× |
и |
( ˆ× (+))h ×)) |
(x |
B( ) |
B x |
|
|
||||||||||
|
( ˆ |
|
( ˆ |
|
)) |
1 |
& |
|
|
1 &2 |
1 |
|
ò |
+ |
2 |
1+) |
(h |
1-)h( |
hdt+ |
- dt= × |
|
|
|
|
( |
( ) |
|
|
|
ò ò |
|
|
|||||||||||
|
|
|
|
|
|
0 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
При мени ви нтегри ровани епо частям впервом и нтеграле, получаем:
( ˆ |
|
( ˆ |
|
|
1 1 |
1 &2 |
|
1 |
|
2 |
1) =(h |
1)h+( |
|
hdt+ |
|
||||
|
)) |
( ( ) |
ò ò |
ò |
|
- |
|||||||||||||
|
0 |
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
|
0 |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ò &2 |
2 ( )=³ 0 1 +h h dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xˆ(t) |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||
Следовательно, функц и я |
|
|
+ |
= -является глобальны м ми ни мумом |
|
|
|
||||||||||||
4 |
|
|
|
||||||||||||||||
вданной задаче. |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
З а да чи для са мо сто ятельно го р еш ения |
|
|
|
|
|
|
|
||||||||||
1. Н айти допусти мы еэкстремали в простейш и х задачах вари ац и онного |
|
|
|
|
|||||||||||||||
и счи слени я : |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
ò & |
|
|
|
|
|
|
= 0. 1)x=( 0, 0)x( ;®extr |
+ ) |
dt× |
= tx( |
) |
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
& 2 |
2 |
|
|
|
|
|
|
|
= 0. |
1)x=( 0, |
0)x( |
;®extr |
|
dt-× x=t |
|||
& |
ò |
|
|
|
|
|
|
|
+) |
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 / 2 |
&3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
& |
ò |
|
|
|
|
|
|
= 1. |
)x=( 0, |
0)x( |
|
;®extr |
+) |
dt× |
=x 2( |
||||
|
|
|
|
2 |
|
|
|||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π / 4 |
& 2 |
2 |
|
|
|
|
|
|
π4 |
= 0. |
)x=(1, |
0)x( |
;®extr |
-) dt |
× x= |
|||
& |
ò |
|
|
|
|
|
|
||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
68
|
π / 2 |
|
|
|
|
|
|
π2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
ò |
& 2 |
|
2 |
|
|
|
|
= 0. |
)x=( 0, |
0)x( |
;®extr |
- ) |
dt- |
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
& 2 |
|
|
|
|
|
= 2. |
|
e)x=(1, |
1)x( |
;®extr |
|
|
-dt× |
=x |
|
x |
|||
& |
ò |
|
|
|
|
|
|
+ |
) |
( |
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
ò & |
|
|
|
|
|
= 1. |
3)x=( 0, |
2)x( |
;®extr |
- |
) |
dt× |
=(1 |
t |
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
& 2 |
|
|
|
|
|
|
= 0. |
e)x=(1, |
1)x( |
;®extr |
|
|
dt× |
=x2( |
|
||||
& |
ò |
|
|
|
|
|
|
+) |
|
||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Н айти допусти мы еэкстремали взадачах Больц а. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
3 |
|
|
4 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
ò |
& |
|
® extr. |
- |
3) x+( 8 |
0) |
(x× = dt |
x x 4 |
|
))1 (x (B |
|
|||||||||
|
|
|
|
|
|
||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
22 |
2 |
|
- 1 ) x(+5 |
0×) |
x(=4 |
dt |
x |
|
))2) x( B( |
|
|
||||
& |
ò & |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
® extr . |
|
|
|
|||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
ò & 2 |
|
2 |
|
|
® extr . |
- 1 sh |
1)+ (x 2× |
=dt) |
x |
(x |
))3(x( B |
|
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
2 |
2 |
|
1 ) +x2( |
× dt= ) |
x |
x ( |
))4) x( B( |
|
|
|
|
||||
& |
ò |
& |
|
|
- |
|
|
|
|
||||||||||||
|
|
|
® extr . |
|
|
|
|
||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
|
2 |
|
2 t |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
ò |
& |
|
|
® extr+ |
. |
1 ) +0 )x (1 )(x +2 ( |
dt |
× )x=2 |
|
x |
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
2 |
2 |
|
1 ) +x( 2 |
× dt= ) |
x |
x ( |
( 6))) x |
B( |
|
|
|
|
|||
& |
ò |
& |
|
|
- |
|
|
|
|
||||||||||||
|
|
|
® extr . |
|
|
|
|
||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
− |
1)x(® extr .( 0) x+ |
|
x e2+32 |
|
|
|
|
|
|
|
|
|
|||
& |
ò |
& |
|
|
|
|
× |
e4= |
dt |
|
x |
e |
)) 7( x( |
||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ 9. Реш ение за да ч ма тема тическо го пр о гр а ммир о в а ния ср едств а ми EXCEL
В данном параграфепри водятся алгори тмы реш ени я задачли нейного и нели нейного программи ровани я средствами EXCEL.
Реш ение за да ч линейно го пр о гр а ммир о в а ния
Реш ени е задачи ли нейного программи ровани я в среде EXCEL осущ ествляется всоответстви и со следую щ и м алгори тмом
1.Ввод условийзадачи
1.1.Создание формы длявводаусловийзадачи. Ф ормадля вводауслови й задачи
+ |
2 +2 1 +1 n x nc→ |
(min)x c c x |
max |
... |
69
|
|
|
|
|
+ |
|
+ |
|
+ |
|
|
n |
n |
£ |
³ =) b1, |
( |
|
|
x |
a1 ... |
x2 |
a12a |
x 1 |
|
11 |
|||||
|
|
|
|
|
+ |
|
+ |
|
+ |
|
|
n |
n |
£ |
³ =) b, |
( |
|
|
x |
a ... |
x |
a a |
x |
|
1 |
2 |
||||
|
|
|
|
|
|
|
|
|
… . |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
2 |
22 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
³ =) b, |
( |
|
|
x |
a ... |
x |
aa |
|
x |
|
|
|||||
|
|
|
|
|
+ |
|
+ |
|
+ |
1 |
|
|
£ |
|
|
m |
|
|
||||||||||||
|
|
|
|
|
|
|
2 2 |
|
1 |
, … x, |
|
|
|
|
m |
|
|
|
n |
mn |
m |
|
|
|
|
|||||
|
|
|
|
≤ ≤ dl , |
x≤ ≤ dl |
2 |
2 |
≤ ≤ dl |
n |
x |
n |
|
|
|
|
|
|
|
|
|||||||||||
|
и меетследую щ и й ви д |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
ПЕР ЕМ ЕННЫ Е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
им я |
|
им я 1 |
им я 2 |
… |
им я n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зна че ние |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ниж н. гр |
|
l1 |
l2 |
… |
ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в е р х. гр |
|
d1 |
d2 |
… |
dn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф ункция, |
|
|
|
|
на п р а в ле ние |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
р е а лизую |
щ |
а я |
|
|
о п т им иза ции |
|
|
|
|
|
|
|
|
|||||||||
|
ко эф.в Ц Ф |
|
с 1 |
с 2 |
… |
c n |
|
це ле в ую |
функцию |
|
(m ax , m in) |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
О ГР |
А НИ ЧЕНИ Я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
в ид |
|
|
|
|
|
|
ле в а я |
ча |
с т ь |
|
|
|
зна к |
|
|
|
п р а |
в а я ча с т ь |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Ф ункция,р е а лизу- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
на зв а ние |
|
|
|
|
|
|
ю |
щ |
а я |
ле в ую |
ча |
с т ь |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
о гр а ниче ния 1 |
a11 |
a12 |
… |
a1n |
|
1-го |
о гр а ниче ния |
|
|
|
|
|
|
b1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Ф ункция, р е а лизую |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
на зв а ние |
|
|
|
|
|
|
щ |
а я ле в ую |
ча с т ь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
о гр а ниче ния 2 |
a21 |
a22 |
… |
a2n |
|
2-го |
о гр а ниче ния |
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
||||||||
|
… |
|
… |
… |
… |
… |
|
… |
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
… . |
|
|
|
|
|
|
|
|
на зв а ние |
|
|
|
|
|
|
Ф ункция, р е а лизую |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
о гр а ниче ния |
|
|
|
|
|
|
щ |
а я ле в ую |
ча с т ь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
m |
|
a31 |
a32 |
… |
a3n |
|
m -го о гр а ниче ния |
|
|
|
|
|
|
b3 |
|
|
|
|
|
|
|
||||||||
|
Ввод исходных данных. Заполняю тся |
|
ячейки , |
|
содержащ и е: |
ни жни е и |
|
|
|
|
|
|
||||||||||||||||||
|
верхни е |
грани ц ы переменны х, |
|
коэффи ц и енты |
ц елевой |
функц и и , |
|
|
|
|
|
|||||||||||||||||||
|
коэффи ц и енты |
ограни чени й, |
|
знаки |
|
ограни чени й, направлени е |
|
|
|
|
|
|||||||||||||||||||
|
опти ми зац и и ц елевой функц и и . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2. Ввод зависимост ей из |
мат емат ической модели. |
Заполняю тся ячейки |
|
|
|
|
|
|
||||||||||||||||||||||
|
содержащ и е: функц и ю , |
реали зую щ |
ую ц елевую |
функц и ю |
задачи, |
функц и и |
|
|
|
|
|
|
||||||||||||||||||
|
реали зую щ и елевы ечасти ограни чени й задачи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2.1. Ввод зависимост и дляцелевойфункции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2.1.1. П омест ит ь курсор в ячейк у, |
от веденную |
под значение целевой |
|
|
|
|
|
||||||||||||||||||||||
|
функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
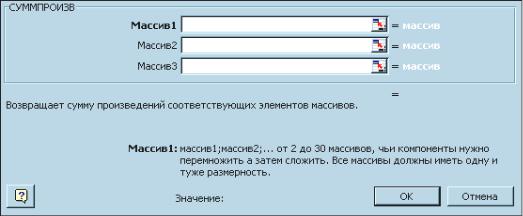
2.1.2.Выбрат ь кнопк у М аст ер ф ункций.
2.1.3.Выбрат ь в окне К ат егориякат егорию мат емат ические
2.1.4.Выбрат ь функцию СУ М М ПР О ИЗВ.
70
2.1.5. З аполнит ь диалоговое окнофункции СУ М М ПР О ИЗВ.
В масси в 1 нужно занести ди апазон ячеек, содержащ и х значени я
переменны х. В масси в 2 – ди апазон ячеек, содержащ и х коэффи ц и енты
целевой функц и и .
3.2.Ввод зависимост ейдлялевых част ейограничений.
3.2.1. П омест ит ь курсор в ячейк у, от веденную под левую част ь ограничения.
3.2.2.Выбрат ь кнопк у М аст ер функций.
3.2.3.Выбрат ь в окне К ат егориякат егорию мат емат ические.
2.1.6.Выбрат ь функцию СУ М М ПР О ИЗВ.
2.1.7. |
З аполнит ь |
диалоговое окно для функции СУ М М ПР О ИЗВ. |
Занести |
в масси в 1 |
ди апазон ячеек, содержащ и х значени я переменны х |
(и спользовать при |
этом абсолю тны е ссы лки ), в масси в 2 – ди апазон |
|
ячеек, содержащ и х коэффи ц и енты данного ограни чени я. |
||
2.1.8. |
Копироват ь содерж имое ячейк и в буфер |
|
2.1.9. |
Вст авит ь содерж имое буфера в ячейк и, от веденные под левые |
|
част и ост альных ограничений.
4. Ввод основных парамет ров модели в диалоговомокне Поиск решения. 4.3. Войт и в меню Сервис и выбрат ь пунк т Поиск решения.
