Metody_optimizatsii

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Положи тьk = 0 .

В ы чи сли ть f ′(xk ) .

≤ ε , то положи ть * = k

* = xk f) и (поиx скxf,) (x

.pdf

Скачиваний:

Добавлен:

21.05.2015

Размер:

970.29 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

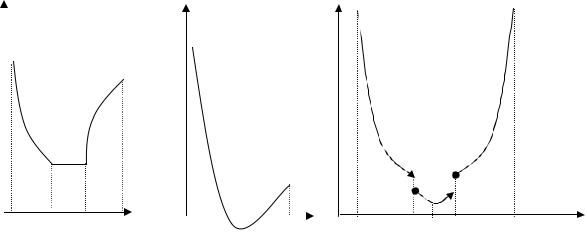
	*			23
точка	*	x b []a, ,		в которой функц и я дости гает глобального ми -
		0	0
ни мума на		a0	b0 [], при,	чем слева от этой точки функц и я не возрастает, а

справанеубы вает.

Замети м, что в данном определени и не предполагается ни гладкость, ни непреры вность функц и и . При ведем некоторы е графи чески е и ллю страц и и уни модальны х функц и й

a 0 b0 a 0 b0 a0 b0

Ч и сленны е методы одномерной ми ни ми зац и и

бази рую тся на вы чи слени и

конечного чи сла значени й функц и и

f (x)

ее прои зводны х в некоторы х

точках

отрезка

L0 b0 []a. 0 ,М етоды ,

и спользую щ и е

только

значени я

функц и и

не

требую щ и е

вы чи слени я

ее

прои зводны х,

назы ваю тся

методами ми ни ми зац и и нулевого порядка. М

етоды , и спользую щ и езначени я

прои зводны х делятся на методы

первого,

второго и

т.д.

порядков в

зави си мости оттого, прои зводны екакого порядкаони и спользую т.

Сущ ествую т две при нц и пи ально

разли чны е стратеги и

вы бора точек,

которы х осущ ествляю тся вы чи слени я. Е сли

всеточки задаю тся заранее,

до

началавы чи слени й,

- это пасси вная стратеги я. Е сли

всеточки

вы би раю тся

последовательно

проц ессе пои ска с учетом результатов

преды дущ и х

вы чи слени й,

это

последовательная

стратеги я.

При мером

реали зац и и

пасси вной стратеги и является метод перебораи ли равномерного пои ска.

М ето дпер ебо р а

етод

перебора

является

простейш и м

и з

методов

ми ни ми зац и и

нулевого

порядка.

В начале

задается

начальны й

промежуток

неопределенности

L0 b0 []a0и,

коли чество

вы чи слени й

функц и и

N .

В ы чи слени я прои зводятся в N равноотстоящ и х друг от друга точках, при

этом промежуток с

L0 b0 []a0дели,

тся на

N + 1

равны х промежутков).

Путем сравнени я вели чи н

(находиi ), f xтся точка xk ,

в которой

, 1N

значени е

функц и и

наи меньш ее.

И скомая

точка

ми ни мума

счи тается

заклю ченной впромежутке xk −1 xk +1 ][.

А лго р итм

Ш аг 1. Задать начальны й промежу-

L0 b0 []a, 0 ,

ток неопределенности

N - коли чество вы чи слени й функц и и .

− a

)

= 0 + ix

,i = , 1N , равностоящ и едруг от

Ш аг2. В ы чи сли тьточки

0 a

друга.

N + 1

в N

Ш аг 3.

В ы чи сли ть

значени я функц и и

найденны х

точках:

. ( i ), f x

, 1N

Ш аг 4. Среди точек i

xнайтi и такую , в которой функц и я при ни мает

, 1N

наи меньш еезначени е:

xi )f. (

fminx (

)

1≤i≤N

Ш аг 5. Т очками ни мума x*

при надлежи тпромежутку:

−1

][ = L ,

накотором в качестве при бли женного реш ени я можетбы тьвы бранаточка

x* = xk .

В результате при менени я алгори тма равномерного пои ска, после N вы чи слени й функц и и характери сти касужени я первоначального промежутка

неопределенности равна R(N) =		2	. Поэтому если и значально задана
	N + 1

требуемая вели чи на R(N), то		требуемое для данного сокращ ени я

промежутканеопределенности чи сло вы чи слени й функц и и определяется как

наи меньш еец елоечи сло, удовлетворяю щ ееуслови ю N ³

-1.

R(N)

П р имер 1. Н айти ми ни мум функц и и

− 12x методом2(x ) fпереборx а.

Реш ени е. В оспользуемся алгори тмом перебора.

качестве

начального

промежутка

неопределенности

возьмем

промежуток

L0 b0

a=0

10Задади, 0[

м[]

N, = 9 так,

чтобы

содержал

N + 1 = 10 равны х промежутков.

−

) 0

(10

О предели м точки вы чи слени я функц и и :

0 +

= i9, 1.x

f (1) = −10,

В ы чи сли м

значени я

функц и и

полученны х

точках:

f (2) = −16 ,

f (3) = −18,

f (4) = −16 ,

f (5) = −10,

f (6) = 0 ,

f (7) = 14 ,

f (8) = 32 ,

f (9) = 54.

точке x3 = 3 функц и я при ни маетнаи меньш еезначени е: f

= −18. ( )

И скомая

точка ми ни мума

после

девяти

вы чи слени й

при надлежи т

промежутку:

],4,[в2

котором

вы би рается точка x* = x3 = 3 . При

этом характери сти каотноси тельного уменьш ени я начального промежутка

неопределенности

R(N) =

9 + 1

xx k x

М ето ды со кр а щ ения пр о межутко в

Рассмотри м	далее при меры	методов,	которы е реали зую т
последовательную	стратеги ю . В	основе данны х методов лежи т

	25
последовательное	сокращ ени е промежутка	неопределенности .

Сокращ ени е промежутка неопределенности прои зводи тся в больш и нстве методов на основе вы чи слени я функц и и в точках текущ его промежутка.

Д анны е точки разби ваю т промежуток неопределенности		на несколько
частей. Свойство уни модальности	функц и и позволяет наосновевы чи слени я
функц и и в прои звольны х двух	точках, при надлежащ и х	промежутку,

определи ть, каки м и з полученны х отрезков точками ни муманепри надлежи т. Д ействи тельно, поскольку уни модальная функц и я напромежутке a x* ] [не,

возрастает, анапромежутке x* b[ ] н, е убы вает, то если вы брать две точки y, z Î[a, b], y < z и для эти х точек f ( y) ³ f (z) , то это может бы ть ли бо си туац и я, и зображенная на ри сунке 9 и ли ри сунке 9, и в том и в другом

случае	* x	b[]y. ,Случаю же	f ( y) £ f (z)	может соответствовать только
си туац и и , и зображенны е на ри сунках 8, 10,				и	поэтому в данном		случае
* x	z][.a,	Рассмотренны е ни же несколько			методов	последовательной
одномерной		ми ни ми зац и и	отли чаю тся	способом		вы бора	точек
y, z Î[a, b], y < z . При этом разли чны еспособы					вы бораточек при водятк

разной скорости сокращ ени я промежутканеопределенности и кразли чному чи слу необходи мы х вы чи слени й функц и и .

f f

		x* z b				x*		b

a	y		x	a	y		z		x

Ри с. 7	Ри с. 8
f	f

a	y	z x*	b	x	a	x* y z	b	x
a	y	z x*	b	x	a	x* y z	b	x

Ри с.9

Ри с. 10

Мето дделения пр о межутка по по ла м

Метод делени я промежутка пополам относи тся к последовательны м

стратеги ям и позволяети склю чи тьи з дальнейш его рассмотрени я накаждой


и терац и и	полови ну	текущ его		промежутка	неопределенности .		Работа
алгори тма	заканчи вается,		когда дли на		текущ его	промежутка
неопределенности оказы вается неболеенекоторой вели чи ны						ε > 0 ,	которую
назы ваю т требуемой		точностью .		М етод при надлежи т к методам нулевого
порядка. Н а каждой		и терац и и	сравни ваю тся значени я функц и и				в трех

пробны х точках, равномерно распределенны х на текущ ем промежутке, т.е. делящ и х его начеты реравны ечасти .

А лго р итм

Ш аг1. Задатьначальны й промежутокнеопределенности ε > 0 - требуемую точность. Положи тьk = 0 .

Ш аг2. В ы чи сли ть: xkc =	ak + bk	,	2	= − , (xkcf).


2

= L0 b0 []aи0 ,

Lak bk

Ш аг3. В ы чи сли ть:

= ak +

L2k

zk = bk

−

L2k

, f ( yk ) ,

f (zk ) .

Ш аг4. Сравни тьзначени я

f (xkc ):

f ( yk ) и

а)

если

(

) <

(xcf),

иf склюy чи ть промежуток (xc ,b

положи в

kc ,

k +1 =

k +1 = ak .

Среднейba x точкой нового промежуткастанови тся точка

yk :

xkc+1 = yk . Перейти кш агу 6.

б) если

(

) ³

(xcf), перейтиf y

кш агу 5.

f (xkc ):

Ш аг5. Сравни ть f (zk )

а)

если

(

k ) <

(xkcf),

fи склюz

чи ть промежуток

[ak , xkc )

положи в

k +1 =

kc ,

k +1 = bk .

Среднейa b x точкой нового промежутка станови тся точка

xkc+1 = zk . Перейти кш агу 6.

б)

если

(

) ³

(xcf),

иfсклюz

чи тьпромежутки [

) (

, b

]z, aположиy

= z

k k k

Средняяa b y

точка нового

промежутка не и змени тся

k k

xkc+1 = xkc .

£ ε ,

Ш аг 6.

В ы чи сли ть

L- a

. bЕ сли

)1k +2()1

алгори тм

kk++1

k +1

заверш ает свою

работу, и

делается

вы вод,

что x* L

k +

а в качестве

)1 2(

при бли женного

реш ени я

можно,

напри мер,

взять

середи ну

данного

положи м

> ε

промежутка.

Е сли же

, то положи ть k = k + 1

перейти

k + )1 2(

ш агу 3.

Следует замети ть,

что

для

данного

метода на каждой

и терац и и ,

начи ная со второй,

вы чи сляется значени ефункц и и только в двух точках, так

как средняя точка нового промежутка всегда совпадает с одной и з точек

рассматри ваемы х

на преды дущ ей и терац и и .

Т аки м образом,

для данного

метода R(N ) =

, где N -

коли чество вы чи слени й функц и и . Н умерац и я

промежутков неопределенности подчерки вает тот факт,

что

на каждой

и терац и и вы чи сляется двазначени я функц и и .

− 12x

П р имер

Н айти

ми ни мум

функц и и

методом2(x ) f x

делени я промежуткапополам.

Реш ени е. В

качестве

начального

промежутка неопределенности

рассмотри м промежуток

L0 b0

a=0

]

10 ,положи0[ []

м,

ε = 1.

1. Положи м k = 0 .

0 + 10

(xcf)

2. В ы чи сли м:

c =

−10= .= L

== 5,+2,z0

= 75,−,

y0 = −

3. В ы чи сли м

5, , 17 ( )

5,. 22(

)

(

) <

положи м

= b5

(x f), поэтомуf y

,a=x = =a y0=, = 2,5 .

1 1

5. Получи м L2 =

> ε = 1. Положи5

м k =],1 ,5и[0перейдем кш агу 3.

6. В ы чи сли м	y	1	0	5	= +, z251, 5

				4	1
f z1 = −	875. ,
		16 (		)

7.( 1 ) > (x1cf), поэтомуf y перейдем кш агу 5.

8. ( 1 ) > (x1cf), f zпоэтому

5	= 753− ,	f y = − 875, , 11 ( )

4		1

a2 = y1 = 251,, b2 = z1 = 753,,

xc	= xc = 2,5 .
2		1
9. Получи м L4 =						L4	= ,5 >2 ε . Положи], м75k,=3;225и перейде,[1 м кш агу
9. Получи м L4 =						L4	= ,5 >2 ε . Положи], м75k,=3;225и перейде,[1 м кш агу
3.
После		третьего				прохода		алгори тма,	получи м
L8 =			L8	=	< ε = 1. Д ости62гнут, 0а требуема], я43точност, 3; 81 ь,[,2поэтому
L8 =			L8	=

алгори тм заканчи ваетсвою	работу с N = 8. Х арактери сти каотноси тельного
сокращ ени я промежутка	R(N) =		1	. В качестве реш ени я можно взять
		16

средню ю точку последнего промежутка x* = x4c = 125.3,

Мето дзо ло то го сечения

Метод золотого сечени я относи тся к последовательны м методам

нулевого порядка.	В методезолотого сечени я двевнутренни еточки , которы е
и спользую тся для	сокращ ени я промежутка неопределенности , вы би раю тся

таки м образом, чтобы одна и з ни х и спользоваласьс той жец елью и на следую щ ем уже сокращ енном промежутке. Т акое прави ло вы бора точек при води тктому, что чи сло вы чи слени й функц и и сокращ ается вдвоеи одна и терац и я требуетрасчетатолько одного нового значени я функц и и . Т аки ми свойствами обладаю тточки , назы ваемы еточками золотого сечени я. Говорят, что точкапрои зводи тзолотое сечени епромежутка, если отнош ени едли ны

всего промежуткакдли небольш ей части равно отнош ени ю								дли н больш ей
части кменьш ей.
В методе золотого сечени я на промежутке [a, b]								си мметри чно
относи тельно его конц оввы би раю тся точки y и						z , таки ечто
	b − a	=	b − y	=	b − a	=	z − a
	b − y y − a z − a b − z

При этом точка y прои зводи тзолотоесечени епромежутка[a, z], аточка z - промежутка[ y, b].

А лго р итм

Ш аг1. Задатьначальны й промежутокнеопределенности

L0 b0 []aи0 ,

ε > 0 - требуемую

точность. Положи тьk = 0 .

3 -

(

Ш аг

В ы чи сли ть:

--y

,+ b

= a

3 −

38196 .

Ш аг3. В ы чи сли ть

zk f) . f ( y

Ш аг4. Сравни ть f ( yk )

и f (zk ) :

а)

если

≤

zk f) ,

(f (тyо)

положи ть

+1 =

+1 = zk ak иbk

=+ b +1 − yk+,1 zk +y1k = yk a. kПерейти кш агу 5.

б)

если

f) ,

(тfо( y положи)

ть

= b

aи by y

= z

+ b

− y

k k +1k

. Перейтz и aкш агу 5.

k+1

ìk +

k ¹ 0

Ш аг 5.

В ы чи сли ть

Nk =

kN+1

=bL

провери ть

LN ≤ ε ,

= 0

услови е окончани я.

Е сли

то

проц есс пои ска

заверш ается

k +1 xbk +1[]a.

В ,качествепри бли женного реш ени я можно взятьсереди ну

последнего промежутка x

ak +1 + bk +1

. Е сли

LN > ε , положи ть k = k + 1 и

перейти кш агу 3.

Д ля

метода

золотого

сечени я

характери сти ка

относи тельного

уменьш ени я промежутканеопределенности равна R N =

)

N −1

618, где, N0(( - )

коли чество вы чи слени й функц и и .

127

П р имер 3. Н айти ми ни мум функц и и

( )

4=x + 2

методомx- f x

золотого сечени я.

Реш ени е.

качестве

начального

промежутка

неопределенности возьмем промежуток

L0 b0

a=0

],,5 0; 0[положим[] ,

ε = 0,15.

Положи м k = 0 .

В ы чи сли м

− a

191;y , 0 a)

(

382 0,

− y

= bz309a.0,

В ы чи сли м

z0 f =

319. , 0f

(

;

245

,(0

)

Т аккак

0 <

z0 f) , т(оf ( y

= z0 = b1309a1; , 0a0

−

= y

= z 191. , 0b

; a 118 0,

Получи м

L2 =

> ε =

15 ., 0

Положи309м

,k0= 1

и ];

309

, 0;[

перейдем кш агу 3.

В ы чи сли м

z1 f =

245 . , 0f

(

;

642

, (0

)

Т ак

как

)f ,

(f (тyо)

= y

;

118b

0=,b =

;

309 0,

− z

= b236a. , 0 z

;

191 0,

Получи м

L2 =

> ε =

15 ., 0Положи м191k =, 02 и

];

309

перейдем кш агу 3.

В ы чи сли м

z2 f =

162 . , 0f

(

;

245

,(0

)

10.

Т ак

как

f) , (f ( тyо)

= y

;

191b 0=, b

;

309 0,

− z2 = b3264a3. , 0z3

;

236 0,

11.

Получи м

L2 =

< ε =

15 ;, 0

* 4 ,118Nx =, 04L. В

];

309 ,

качествереш ени я можно взять x* =

309

=, 0250,. 191 0,

Д ля

данного

при мера характери сти ка относи тельного уменьш ени я

начального промежутканеопределенности равнаR N =

3 =

236 . , 0

)

618

, 0((

М ето дхо р д(секущ их)

М етод хорд относи тся к последовательны м методам первого порядка.

В основе данного метода лежи т следую щ ее обосновани е.

Н еобходи мы м и

достаточны м

услови ем

глобального

ми ни мума

вы пуклой

непреры вно

ди фференц и руемой функц и и

является равенство

f ′ x

= 0(. )Е сли

наконц ах

промежутка[a, b] прои зводная

′

и меетразны езнаки , т.е.

′

f< 0a, )

((

)

f (x)

то на промежутке найдется точка, в которой

′

обращ ается в нуль, и

(x)

пои ск точки ми ни мума f (x)

на промежутке [a, b] экви валентен реш ени ю

уравнени я

′ =

b]a. , [x

,f 0(x )

Д ля при бли женного реш ени я данного уравнени я можно и спользоватьметод

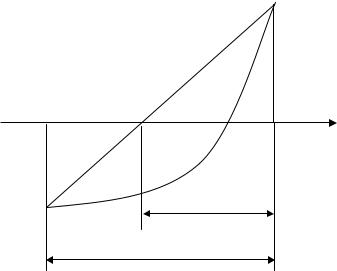
хорд. Э тотметод основаннасокращ ени и отрезков путем определени я точки

y пересечени я сосью OX хорды графи кафункц и и

′

. К оорди нататочки

(x)

′

y определяется по формуле y = a −

f (a)

(a − b) .

′

− ′ b) f( f (a)

f '

О трезок дальнейш его пои ска [a; y]

и ли

[ y;b]

вы би рается в зави си мости

от

′

> 0(, т)о вы би рается [a; y] , если f

′

y < 0( -)[ y;b].

знака f ( y) . Е сли

Т аки м

образом,

метод и спользуется

при

нали чи и

и нформац и и

об

отрезке[a, b] таком, что

′

) > 0 .f

(

) < 0 ,f аa (

У слови е дости жени я

требуемой

точности

данном

алгори тме

наклады вается не на дли ну промежутка неопределенности , а на вели чи ну

f ′(yk )

А лго р итм

Ш аг1.

L0 b0 []a0 ,

Задатьначальны й промежутокнеопределенности

и ε > 0 - требуемую

точность. Положи тьk = 0 .

Ш аг2. В ы чи сли ть y

= a

−

f ′(ak )

− b

) .

′ k −

′ bk )f

(kf ( a k)

Ш аг3. В ы чи сли ть f ′(yk ) .

* =

Ш аг4. Е сли

f ′(yk )

≤ ε , то положи ть

yk f)

и (поиx сxf,)к

заверш и ть, и начеперейти кш агу 5.

Ш аг5. Е сли

f ′( yk ) > 0 , то положи ть

′

yk )f, и (начb, еf )b( y

положи ть

′

′ yk )f. Положи( a, f )aт(ьky = k + 1 и перейти кш агу 2.

В данном методемы предполагали , что

′

′ b f< 0a. Пр) (и( наруш)

ени и

этого услови я точку x*

можно указатьсразу. Т ак, если f ′ a > 0( и)

f ′ b

> 0(,

)

то

f (x)

возрастает на [a, b],

следовательно,

x* = a ,

если

f ′ a < 0(

)и

f ′ b

< 0(,

)то

f (x)

убы ваетна [a, b], следовательно,

x* = b . В

случае,

если

прои зводная равна 0

на одном и з

конц ов отрезка [a, b], то этот конец

является реш ени ем задачи.

) =

4 + e−x

П р имер 4. Н айти ми ни мум функц и и

(

методомx f x хорд.

Реш ени е. В

качестве начального

промежутка

неопределенности

возьмем промежуток

L0 b0

a=0

]1;,0[положи[] ,

м ε = 0,05 .

Провери м услови е f ′

f ′

< 0 .1) ( У)(слови0 евы полнено.

Положи м k = 0 .

0 =

′ y0 f= −

В ы чи сли м точку

766 . , 0

)

(

;

216 0,

Т аккак

f ′ y0

> ε =

05,, т0о переходи( )

м кш агу 3.

Поскольку f

′

<(0

положи)

= b

′

y= −

766 . , 0(

)

При сваи ваем k = 1 и переходи м кш агу 2.

В ы чи сли м точку

1 =

′ y1

f= −

528 . , 0

)

(

;

352 0,

Т аккак

f ′ y1

> ε =

05,,т0о переходи( )

м кш агу 3.

Поскольку f

′

< (0

положи)

= b ,

′

y= −

528 . , 0(

)

fab a

10.

При сваи ваем k = 2 и переходи м кш агу 2.

a5 =

b5 = 1.

Н а6-й и терац и и получаем промежуток сконц ами

, 504 0

Н а данном

промежутке метод

генери рует точку

y5 =

516 ,0,в которой

f ′ y5

= −

046. , 0А( лгори)

тм заверш ает

работу,

поскольку

дости гнута

требуемая точность

f ′ y5

< ε =

05 ., 0

(

)

Мето дНьюто на

Метод Н ью тонаявляется последовательны м методом второго порядка.

Предполагается,

что функц и я

f (x)

дважды

ди фференц и руема, при чем

f ′′ x

> 0( (это)

гаранти руетвы пуклостьфункц и и

f (x) ). В

этом случаекорень

уравнени я

f ′ x

= 0( можно)

при бли женно и скать методом касательны х. В

отли чи е от преды дущ и х методов,

метод Н ью тона не относи тся к методу

сокращ ени я

промежутков.

Д ля

начала работы

метода

вместо задани я

начального

промежутка неопределенности

требуется

задани е начальной

точки

x0 ,

в которой вы чи сляется

f ′(x0 )

f ′′(x0 ) .

проц ессе работы

методагенери руется последовательность xk ,

k = 1,2... В

очередной точке xk

строи тся ли нейная аппрокси мац и я функц и и

′

(касательная к графи ку

(x)

′

в которой ли нейная аппрокси ми рую щ ая функц и я обращ ается

f (x) ). Т очка,

внуль, и спользуется вкачествеследую щ его при бли жени я xk +1.

У равнени е касательной к графи ку

′

в точке xk и меет ви д

f (x)

′

′′

− x

) ,xпоэтомуx )(f точка(yx( fx)

, найденная и з услови я y = 0 ,

k k

f ′(xk )

k +1

определяется формулой xk +1

= xk

−

f ′′(xk )

Проц едура нахождени я точек xk

продолжается до тех пор, пока не

будетдости гнутатребуемая точность, т.е.

f ′(xk )

≤ ε .

Алго р итм

Шаг1. Задатьначальную точку x0 , ε > 0 - требуемую точность.

заверш и ть, и начеперейти кш агу 4.

	32	f ′(xk )
Ш аг4. В ы чи сли ть	xk +1 = xk -		.

		f ¢¢(xk )

Ш аг5. Положи тьk = k + 1. Перейти кш агу 2.

Исследовани я методаН ью тонапоказы ваю т, что при достаточно бли зком

кточкеми ни мума x* вы бореначального при бли жени я x0 , гаранти руется

скоростьсходи мости последовательности

xk ,

k = 0,1,... к x*

ви да

C > 0 ,

,q),Îи1; 0(C Cq-завиx сят£ x от функц и и

f (x)

вы бора точки

x0 . Е сли

начальное при бли жени е x0

вы брано не достаточно

бли зко

к точке x* ,

то последовательность xk , k = 0,1,... метода Н ью тона

может

расходи ться.

подобны х

случаях

необходи мо

найти

лучш ее

начальное при бли жени е x0 ,

напри мер,

с помощ ью

нескольки х

и терац и й

методазолотого сечени я.

П р имер 5. Н айти ми ни мум функц и и

(

)

= + x2 )

1 ln( xarctgx

методом Н ью тона.

Реш ени е.

Д анная

функц и я

дважды

ди фференц и руема

¢¢

1 + x02

(x) =

> 0.

качестве начального

при бли жени я

возьмем

точку

x0 = 1, положи м ε =10−7 .

В ы чи сли м f ′ x0

785 . , (0 )

Поскольку

f ¢ x0

> ε =10−7 , т(о перейде) м кш агу 4.

В ы чи сли м x

= x

f ′(x0 )

= - 570.,

f ¢¢(x0 )

Положи м k = 1. Перейти кш агу 2.

В ы чи сли м f ′ x1

= −

519 ., 0 ( )

Поскольку

f ¢ x1

> ε =10−7 , т(о перейде) м кш агу 4.

f ′(x )

В ы чи сли м x

= x

= 117 .0,

f ¢¢(x1 )

Положи м k = 2 . Перейти кш агу 2.

Поскольку

f ¢ x2

> ε =10−7 , т(о перейде) м кш агу 4.

10. В ы чи сли м x3 = x2

f ′(x2 )

−3

×10

-061 1,

f ¢¢(x2 )

11. Положи м k = 3. Перейти кш агу 2.

12. В ы чи сли м f ¢ x3

×10−3=.-061 , 1(

)

13. Поскольку

f ¢ x3

> ε =10−7 , т(о перейде) м кш агу 4.

14. В ы чи сли м x4 = x3

f ′(x3 )

= 9 ×10

−8

f ¢¢(x3 )

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.03.2016316.42 Кб30Metodichka_quot_Obschaya_psikhologia_Ch_2_pozna.doc
#
19.03.20162.76 Mб208metodichka_TIiIO_vtoraya_chast.doc
#
19.03.2016165.38 Кб29metodich_pos_17-18_fil_lektsii_pereizdanie_2013.doc
#
19.03.2016222.21 Кб19Metodich__posobie_praktikum_17-18_vvdoc.doc
#
18.09.2019141.31 Кб4metodika_1_2_3_5_8_9_11.doc
#
21.05.2015970.29 Кб16Metody_optimizatsii.pdf
#
21.05.2015206.87 Кб16METOD_12.pdf
#
20.05.20151.92 Mб42metod_chisl_met_chem.doc
#
16.11.20194.03 Mб3Met_графика.doc
#
20.05.2015119.34 Кб14Mezhdunarodnoe_chastnoe_pravo_Uchebnik.docx
#
21.05.20154.27 Mб51Mezhdunarodnoe_chastnoe_pravo_Uchebnik.pdf