1.4. Интегрирование методом Эйлера

Данный метод не только очень похож на описанные выше методы нахождения приближенного значения интеграла, но и включает в себя все выкладки и формулы, представленные для методов левых и правых прямоугольников. Решение сводится к нахождению суммы площадей левых прямоугольников, которую мы обозначим S_л, затем находим сумму площадей правых прямоугольников (S_п) и за приближенное значение интеграла функции f(x) принимается величина S_n=(S_л+S_п)/2. Графически (рис.1.5) площадь S_n соответствует сумме площадей трапеций ACGx₁, x₁GIx₂, x₂IMx₃, x₃MOE (поэтому данный метод еще называют методом трапеций) и выражается уравнением:

. (1.6)

1.5. Интегрирование методом Симпсона

По методу Эйлера в каждом интервале вычисляется площадь криволинейной трапеции. Если соединить два интервала, то площадь под графиком функции f(x) на двух интервалах можно аппроксимировать не площадью двух трапеций, а площадью под параболой на сдвоенном интервале (рис.1.6). Этот прием называется методом (правилом) Симпсона (методом парабол). Примем это правило без строгого доказательства. Более подробно это и другие правила изложены в учебниках по численным методам.

В примере, изображенном на рисунке, отрезок [A,E] разделен на 10 интервалов. Длина h одного интервала составляет

h = (E-A)/n = (x_n – x₀)/n,

где n – число интервалов.

Если считать кривую на отрезке [x₀,x₂] параболой, то площадь S под ней можно точно вычислить по формуле:

. (1.7)

Если объединить все интервалы, то получится следующая формула:

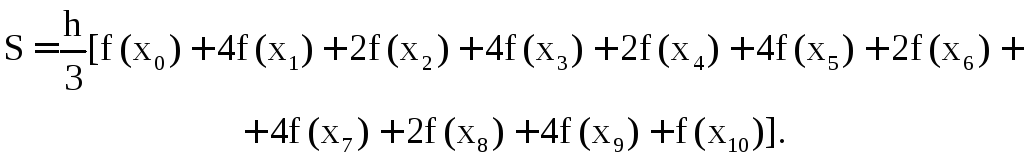(1.8)

или

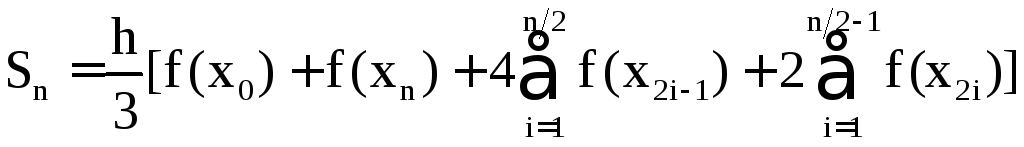. (1.9)

При вычислении величины S_n четные слагаемые удваиваются, а нечетные - увеличиваются в четыре раза.

Как правило, чем меньше длина каждого интервалаh, т.е. чем больше число этих интервалов n, тем меньше различаются приближенное и точное значения интеграла. Это справедливо для большинства функций и вызвано более точной аппроксимацией подынтегральной функции. Для метода трапеций обычно считают, что ошибка приблизительно пропорциональна h², а для метода Симпсона она уменьшается пропорционально длине интервала в четвертой степени, т.е. при увеличении числа интервалов вдвое ошибка уменьшится в 16 раз.

Таким образом, для более точного вычисления интеграла некоторой функции в пределах от А до Е, необходимо не ограничиваться фиксированным значением количества интервалов n, а увеличивать это число после расчета приближенного значения интеграла, например, в 2 раза. Затем нужно опять вычислить новое приближенное значение интеграла и сравнить его с предыдущим результатом. Эту операцию следует повторять до тех пор, пока не будет достигнута заданная точность результата. Выбор критерия, по которому прекращается итерационная процедура, представляет собой наиболее сложную проблему при составлении программы.

Обычно данная проблема решается таким образом: пользователь задает некоторую точность вычислений , и сравнение приближенного значения интеграла с его предыдущим результатом ведется до тех пор, пока разница по модулю в вычислениях интегралов при n и 2n интервалах не будет меньше заданной точности измерений.