
- •I. Численные методы интегрирования
- •1.1. Интегрирование методом левых прямоугольников
- •1.2. Интегрирование методом правых прямоугольников
- •1.3. Интегрирование методом средних прямоугольников
- •1.4. Интегрирование методом Эйлера
- •1.5. Интегрирование методом Симпсона
- •1.6. Интегрирование методом Монте-Карло
- •II. Численное решение нелинейных уравнений
- •2.1. Метод последовательных приближений (Метод простых итераций)
- •2.2. Метод деления отрезка пополам (Метод дихотомии)
- •2.3. Метод Секущих
- •2.4. Метод касательных (Ньютона-Рафсона)
- •III. Решение системы линейных алгебраических уравнений
- •3.1. Решение слау методом Гаусса
- •3.2. Решение слау методом Гаусса-Жордана
- •3.3. Решение слау методом Крамера
- •3.4. Итерационный метод решения системы линейных
- •3.5. Решение системы нелинейных уравнений
- •IV. Приближение нелинейной функции
- •4.1. Приближение линейной функции
- •4.2. Линейная регрессия общего вида
- •4.3. Интерполяция полиномом Лагранжа
- •4.4. Интерполяция с помощью сплайн-функции
- •V. Обыкновенные дифференциальные уравнения
- •5.1. Метод Эйлера решения обыкновенного
- •5.2. Метод Рунге-Кутта четвертого порядка
- •5.3. Методы прогноза и коррекции
- •5.4. Решение систем дифференциальных уравнений
5.3. Методы прогноза и коррекции
Отличительной чертой метода Рунге-Кутта является то, что при вычислении следующей точки (xi+1,yi+1) используется информация только о точке (xi,yi), но не о предыдущих. В методах второго и выше порядков вычисляются значения функции в одной или нескольких промежуточных точках. Наиболее рациональными оказываются методы, сочетающие в себе оба подхода. Такие методы объединены под названием методов прогноза и коррекции. В них сначала «предсказывается» значение yi+1, а затем «корректируется» тем или иным методом. Процесс корректировки итерационный.
Ч тобы
начать решение с помощью метода прогноза
и коррекции, часто используют метод
Рунге-Кутта. Например, если для прогноза
можно взять формулу второго порядка:
тобы
начать решение с помощью метода прогноза
и коррекции, часто используют метод
Рунге-Кутта. Например, если для прогноза
можно взять формулу второго порядка:![]() ,
где верхний индекс (0) обозначает исходное
приближение кyi+1,
т.е. предсказанное значение. Геометрическая
интерпретация прогноза представлена
на рис. 5.2. Находят угол наклона касательной
l1
в
точке (xi,yi),
после чего через точку (xi-1,yi-1)
проводится параллельная прямая l2,
и считают, что искомое предсказанное
значение будет располагаться в точке
пересечения прямой l2
с ординатой xi+1.
,
где верхний индекс (0) обозначает исходное
приближение кyi+1,
т.е. предсказанное значение. Геометрическая
интерпретация прогноза представлена
на рис. 5.2. Находят угол наклона касательной
l1
в
точке (xi,yi),
после чего через точку (xi-1,yi-1)
проводится параллельная прямая l2,
и считают, что искомое предсказанное
значение будет располагаться в точке
пересечения прямой l2
с ординатой xi+1.
Для коррекции
предсказанного значения усредняют
тангенсы наклонов касательных в точках
![]() (l3)
и
(l3)
и
![]() (l1).
Проводят линию l
с полученным
наклоном через точку
(l1).
Проводят линию l
с полученным
наклоном через точку
![]() и находят новое приближение
и находят новое приближение![]() из точки пересечения этой линии с
ординатой
из точки пересечения этой линии с
ординатой![]() (рис. 5.2). Это приближение называют
скорректированным и находят из
соотношения:
(рис. 5.2). Это приближение называют
скорректированным и находят из
соотношения:
![]() .
.
В общем случае, j
– тое
приближение к
![]() вычисляется по формуле:
вычисляется по формуле:
![]() для j
= 1, 2, 3,…
Итерационный процесс прекращается,
когда
для j
= 1, 2, 3,…
Итерационный процесс прекращается,
когда
![]() для некоторого
для некоторого![]() .
.
5.4. Решение систем дифференциальных уравнений
Методы, рассмотренные в данном разделе, легко можно обобщить для системы уравнений первого порядка. Кроме того, уравнения высших порядков можно свести к системе уравнений первого порядка. Например, уравнение второго порядка y = g(y, y, x) можно переписать в следующем виде:

где z – новая зависимая переменная, определяемая вторым уравнением. Таким образом получается система уравнений относительно y и z. Решение данной системы даст функцию и ее производную.
Пусть имеется n
неизвестных функций
![]() ,
i = 1,…,n,
которые описываются n
дифференциальными уравнениями:
,
i = 1,…,n,
которые описываются n
дифференциальными уравнениями:
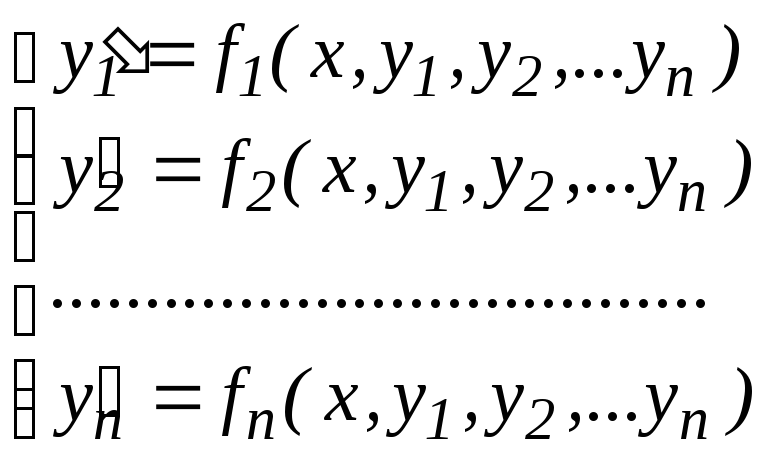 .
.
Начальные условия
для системы уравнений первого порядка
записываются следующим образом:
![]() .
Запись системы в векторной форме
позволяет упростить вычисления, поэтому
вводят:
.
Запись системы в векторной форме
позволяет упростить вычисления, поэтому
вводят:
 ,
,  ,
, .
.
Тогда начальная задача для системы дифференциальных уравнений запишется в виде:
![]() . (5.8)
. (5.8)
Для решения данной системы могут быть применены методы Эйлера и Рунге-Кутта, описанные для решения дифференциального уравнения первого порядка с начальными условиями и заданным шагом изменения x.
Пример 1.
Пусть имеется химическая реакция
![]() .
Уравнение для скорости этой реакции
можно записать соотношением:
.
Уравнение для скорости этой реакции
можно записать соотношением:![]() ,
где
,
где![]() - концентрация к моменту времени
t
от начала реакции; k1
, k2
‑ константы
скорости первой и второй стадии процесса,
соответственно;
- концентрация к моменту времени
t
от начала реакции; k1
, k2
‑ константы
скорости первой и второй стадии процесса,
соответственно;
![]() ‑ начальная концентрация соединенияA.
Необходимо найти зависимость
‑ начальная концентрация соединенияA.
Необходимо найти зависимость
![]() от времени, если заданы начальные
условия:
от времени, если заданы начальные
условия:![]() .
Решение данной задачи сводится к решению
дифференциального уравнения,
соответствующего кинетическому уравнению
системы, с заданными начальными условиями.
Решение это можно осуществить, например,
методом Эйлера согласно (5.5), задав
начальные значения времени и концентраций,
а так же шаг интегрирования. Причем
решение можно уточнять, уменьшая шаг.
.
Решение данной задачи сводится к решению
дифференциального уравнения,
соответствующего кинетическому уравнению
системы, с заданными начальными условиями.
Решение это можно осуществить, например,
методом Эйлера согласно (5.5), задав
начальные значения времени и концентраций,
а так же шаг интегрирования. Причем
решение можно уточнять, уменьшая шаг.
Пример 2.
Имеет место кинетическая система:. .
.
Начальные
концентрации:
![]() = 1.0;
= 1.0;
![]() = 0.0.
Константы скорости k1 = 10;
k2 = 5.
Необходимо найти СA(0.1)
и СВ(0.1).
Указанная кинетическая система
описывается системой дифференциальных
уравнений:
= 0.0.
Константы скорости k1 = 10;
k2 = 5.
Необходимо найти СA(0.1)
и СВ(0.1).
Указанная кинетическая система
описывается системой дифференциальных
уравнений:
 ,
которую можно привести к виду (5.8).
,
которую можно привести к виду (5.8).
Если
![]() ,
,![]() ,
,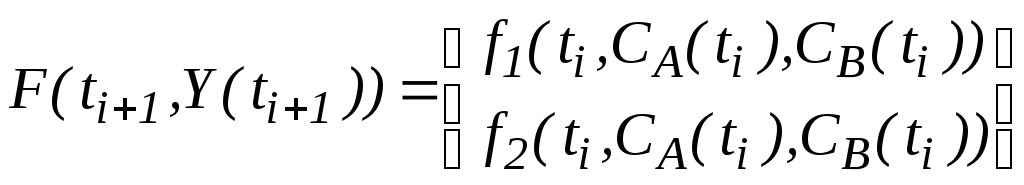 ,
,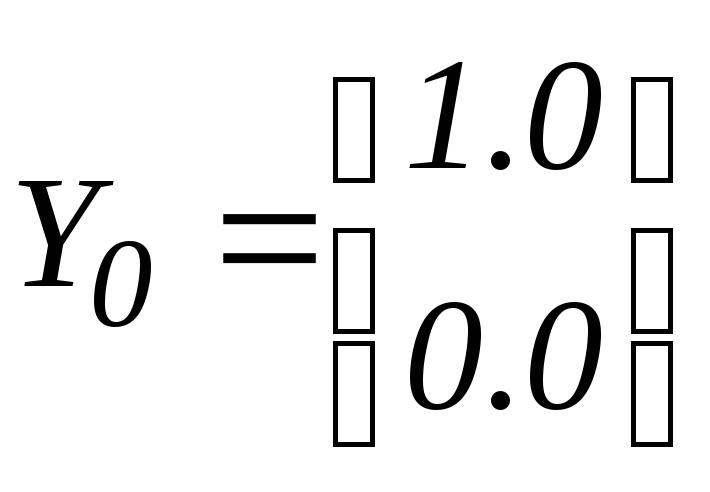 и
и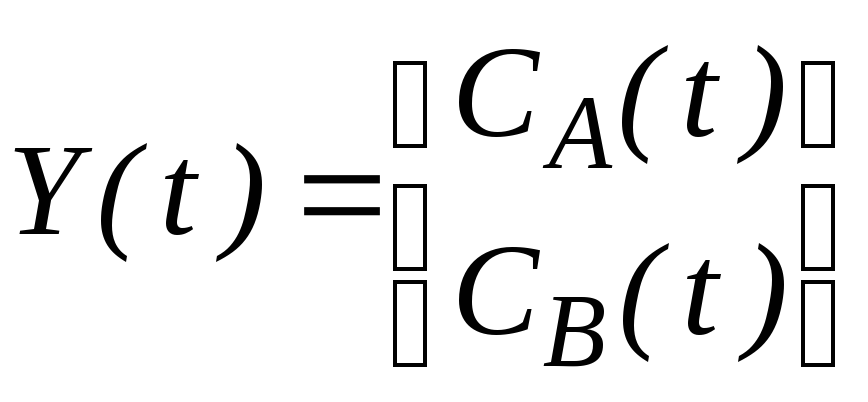 ,
то система принимает вид
,
то система принимает вид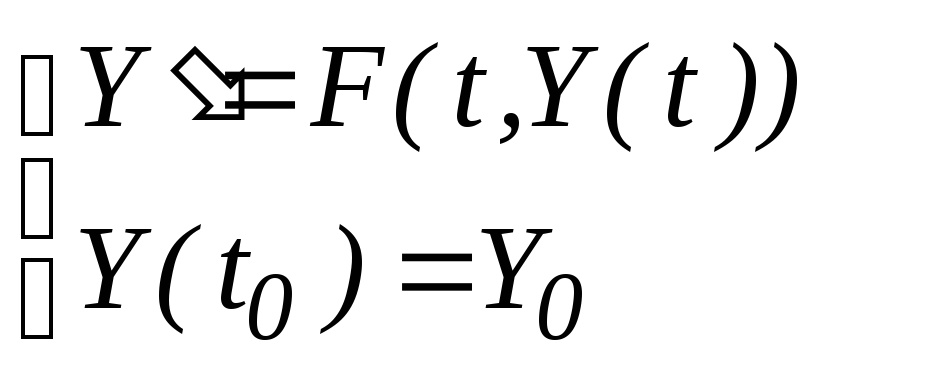 .
Можно найти значения корней этой системы
в виде таблицы значений концентраций
компонентовA
и B
от времени с шагом
.
Можно найти значения корней этой системы
в виде таблицы значений концентраций
компонентовA
и B
от времени с шагом
![]() .
Решать полученную систему можно используя
как метод Эйлера, так и метод Рунге-Кутта.
.
Решать полученную систему можно используя
как метод Эйлера, так и метод Рунге-Кутта.
ЗАДАНИЯ
Степень радиоактивности пропорциональна количеству остающегося радиоактивного вещества. Дифференциальное уравнение, описывающее эту систему записывается в следующем виде:
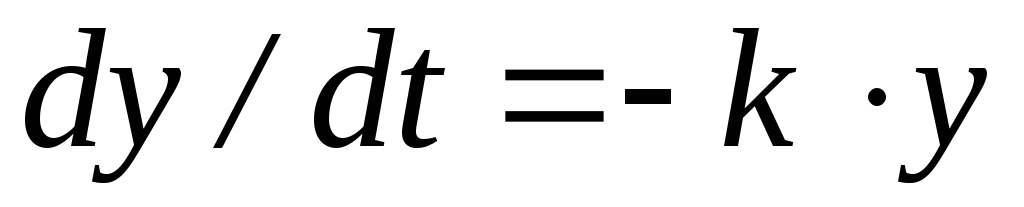 .
Приk = 0.01
и принимая, что начальная масса вещества
.
Приk = 0.01
и принимая, что начальная масса вещества
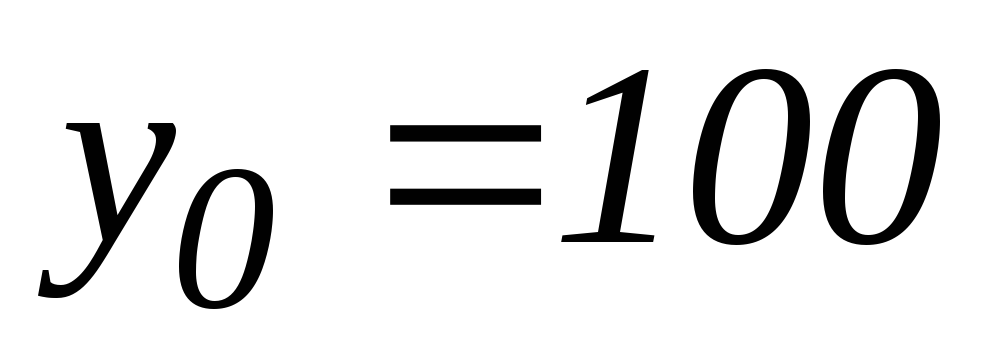 г, найти сколько вещества останется в
момент времени
г, найти сколько вещества останется в
момент времени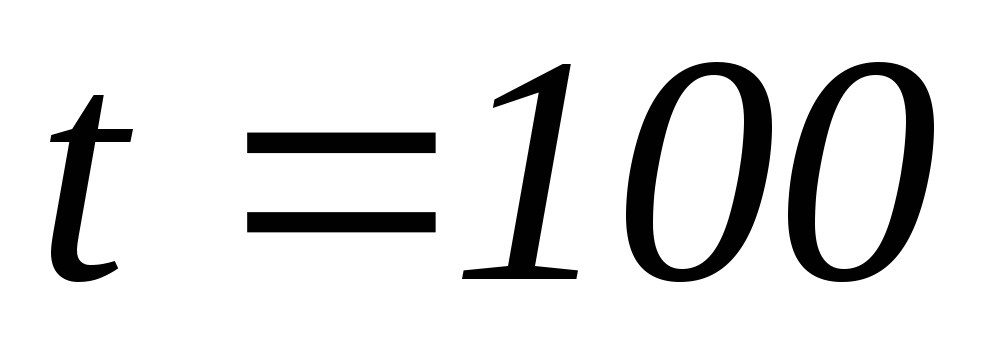 .
Найдите решение численно с помощью: а)
метода Эйлера при
.
Найдите решение численно с помощью: а)
метода Эйлера при
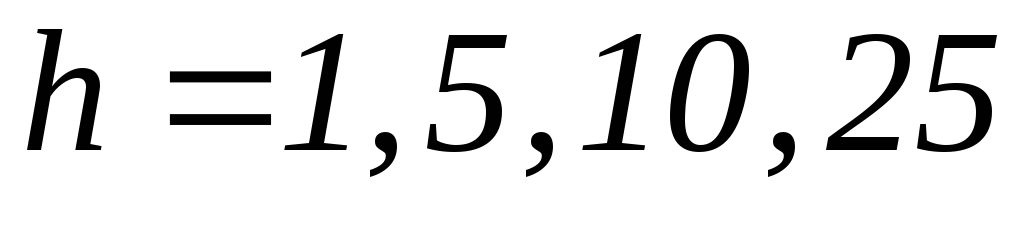 ;
б) улучшенного метода Эйлера при
;
б) улучшенного метода Эйлера при
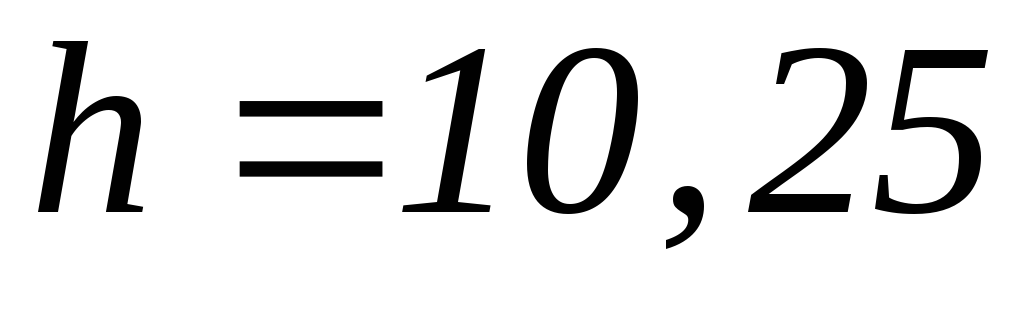 ;
в) метода Рунге-Кутта при
;
в) метода Рунге-Кутта при ;
г) метода прогноза и коррекции с
;
г) метода прогноза и коррекции с ,
если известно, что
,
если известно, что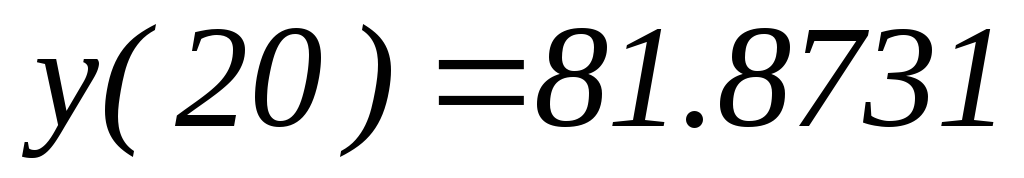 ;
д) метода прогноза и коррекции с
;
д) метода прогноза и коррекции с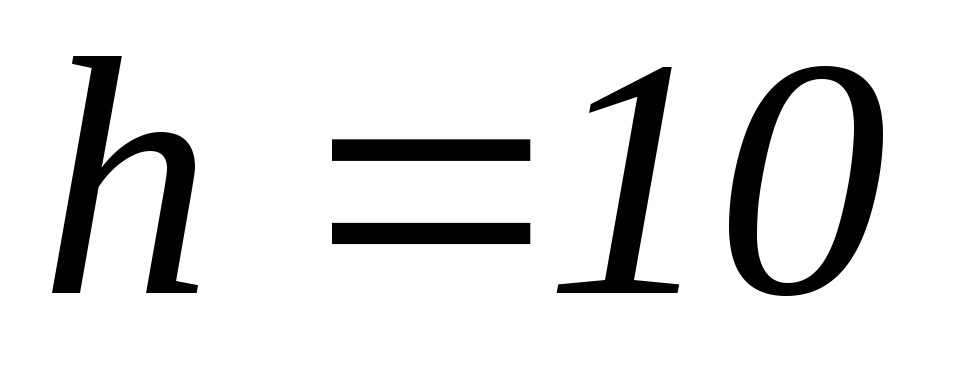 ,
если известно, что
,
если известно, что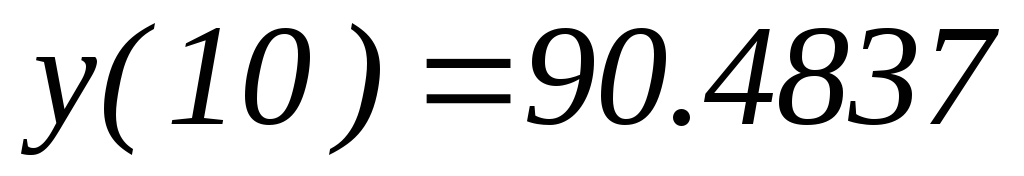 .
.
Пусть скорость радиолиза вещества A пропорциональна заданной безразмерной величине – плотности излучения D.
![]() .
Уменьшение величины D
приближенное описывается экспоненциальной
функцией времени:
.
Уменьшение величины D
приближенное описывается экспоненциальной
функцией времени:
![]() .
Параметры имеют следующие значения:
.
Параметры имеют следующие значения:![]() .
С помощью метода Эйлера найдите
зависимость[A]/[A0]
от времени, задав ее таблично, и вычислите,
какой станет [A]
через бесконечно большой промежуток
времени.
.
С помощью метода Эйлера найдите
зависимость[A]/[A0]
от времени, задав ее таблично, и вычислите,
какой станет [A]
через бесконечно большой промежуток
времени.
Химическая реакция протекает в термически изолированном сосуде. Дифференциальное уравнение, описывающее изменение концентрации исходного вещества, имеет вид:
 .
Для константы скоростиk
выполняется уравнение Аррениуса:
.
Для константы скоростиk
выполняется уравнение Аррениуса:
 .
Температура в реакторе меняется в
зависимости от степени превращения:
.
Температура в реакторе меняется в
зависимости от степени превращения: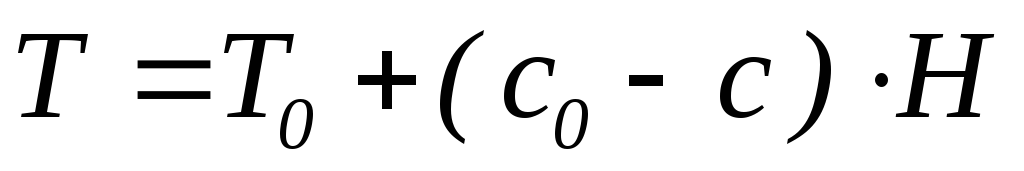 ,
гдеH
– величина, пропорциональная энтальпии
реакции. Методом Рунге-Кутта найдите
таблично заданную зависимость
концентрации c
от времени t
для эндотермической и экзотермической
реакции. Соответствующее дифференциальное
уравнение можно получить из приведенных
ранее уравнений. Решите аналогичную
задачу для реакции второго порядка.
,
гдеH
– величина, пропорциональная энтальпии
реакции. Методом Рунге-Кутта найдите
таблично заданную зависимость
концентрации c
от времени t
для эндотермической и экзотермической
реакции. Соответствующее дифференциальное
уравнение можно получить из приведенных
ранее уравнений. Решите аналогичную
задачу для реакции второго порядка.
Дана реакция разложения a ‑ го порядка:
 .
Тепловой эффект реакции равенH.
Реактор помещен в термостат с температурой
Tb.
Количество тепла, передаваемое от
реактора к термостату, пропорционально
.
Тепловой эффект реакции равенH.
Реактор помещен в термостат с температурой
Tb.
Количество тепла, передаваемое от
реактора к термостату, пропорционально
 .
Зависимость температуры в реакторе от
времени можно описать следующим
дифференциальным уравнением:
.
Зависимость температуры в реакторе от
времени можно описать следующим
дифференциальным уравнением: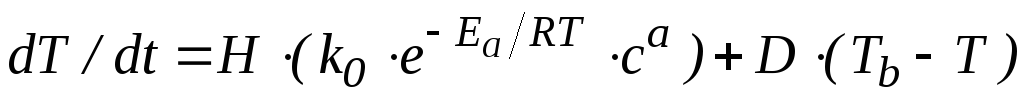 .
ВеличинаH
пропорциональна энтальпии реакции; D
‑ коэффициент теплопередачи через
стенку реактора. Составьте систему
дифференциальных уравнений, описывающую
процессы в реакторе и напишите программу
для решения соответствующей системы
методом Эйлера. Найдите зависимость c
от времени при заданных значениях
параметров
.
ВеличинаH
пропорциональна энтальпии реакции; D
‑ коэффициент теплопередачи через
стенку реактора. Составьте систему
дифференциальных уравнений, описывающую
процессы в реакторе и напишите программу
для решения соответствующей системы
методом Эйлера. Найдите зависимость c
от времени при заданных значениях
параметров
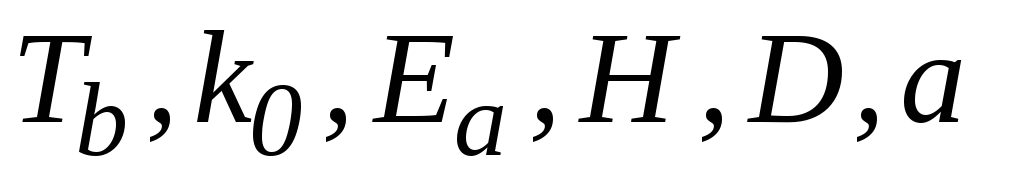 при начальном условии
при начальном условии
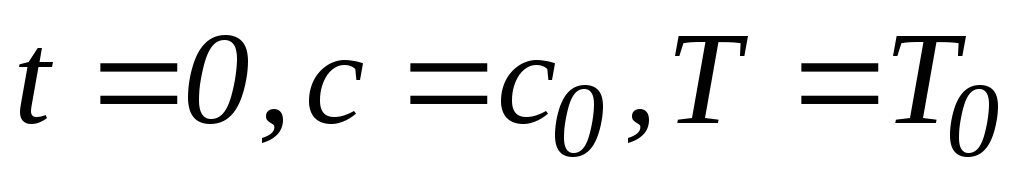 .
Чтобы устранить трудности вычислений
в случае сильно экзотермической реакции
следует отрезок, ограниченный начальным
и конечным значениями аргумента, разбить
на очень большое число частичных
отрезков.
.
Чтобы устранить трудности вычислений
в случае сильно экзотермической реакции
следует отрезок, ограниченный начальным
и конечным значениями аргумента, разбить
на очень большое число частичных
отрезков.
При описании кинетики процессов растворения лекарственного препарата в определенном объеме жидкости различают твердое вещество F и уже растворенное L. При этом исходят из следующих упрощений: а) скорость расходования растворенного вещества пропорциональна количеству вещества, что соответствует реакции первого порядка; б) скорость растворения твердого вещества F пропорциональна величине Fa и разности
 ,
где
,
где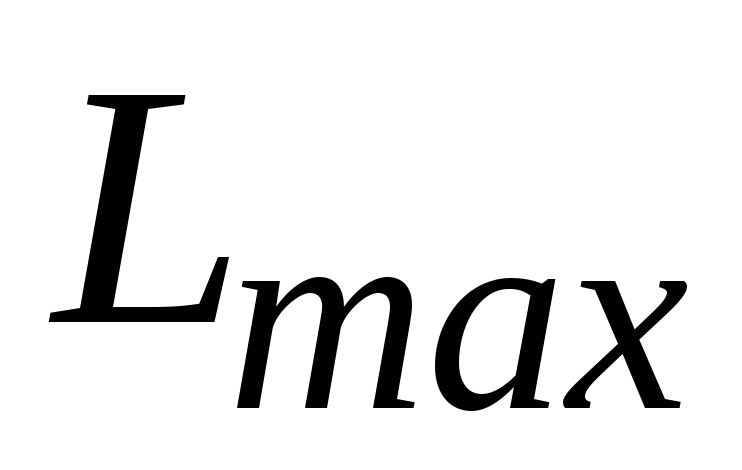 ‑ растворимость препарата в данной
жидкости. Этой модели соответствует
система уравнений
‑ растворимость препарата в данной
жидкости. Этой модели соответствует
система уравнений
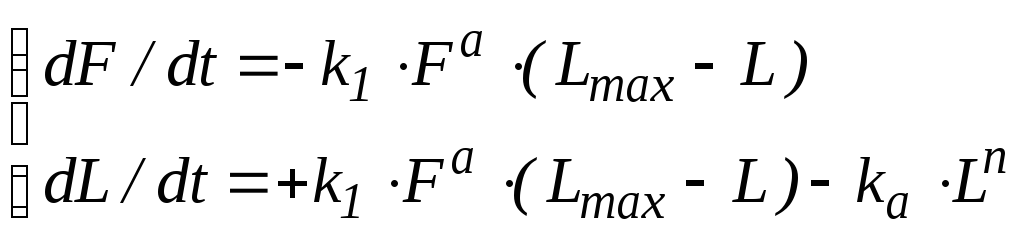 .
.
Методом Рунге-Кутта
рассчитайте зависимость скорости
расходования лекарственного препарата
при следующих значениях параметров:
![]() .
Начальные условия:
.
Начальные условия:![]() .
.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Саутин С.Н. Мир компьютеров и химическая технология / С.Н. Саутин, А.Е. Пунин. – Л.: Химия, 1991. – 144 с.
Эберт К. Компьютеры. Применение в химии / К. Эберт, Х .Эдерер; Пер. с нем. ‑ М.: Мир, 1988. 416 с.
Мак-Кракен Д. Численные методы и программирование на фортране / Д. Мак-Кракен, У. Дорн; Пер. с англ. – М.: Мир, 1977. – 584 с.
Джонсон К. Численные методы в химии / К .Джонсон; Пер. с англ. – М.: Мир, 1983. – 504 с.
Бактнер Л.М. Математические методы в химической технике / Л.М. Бактнер, М.Е. Позин. – Л.: Химия, 1971. – 824 с.
ЭВМ помогает химии: Пер с англ./ Под ред. Г.Вернена, М.Шанона. – Л.: Химия, 1990. – 384 с.
Каханер Д. Численные методы и программное обеспечение / Д. Каханер, К. Моулер, С. Нэш; Пер. с англ. под ред. Х. Д. Икрамова.—М.: Мир, 1998.—575 c.
Бахвалов Н.С. Численные методы: Учеб. пособие для студ. физ.-мат. спец. вузов / И. В. Бахвалов, Н. П. Жидков, Г. М. Кобельков. ‑ СПб.: Лаборатория базовых знаний, 2000.—622 с.
Составители: Протасова Ирина Валентиновна
Крысанов Вячеслав Александрович
Редактор Тихомирова Ольга Александровна
