Стратегический анализ

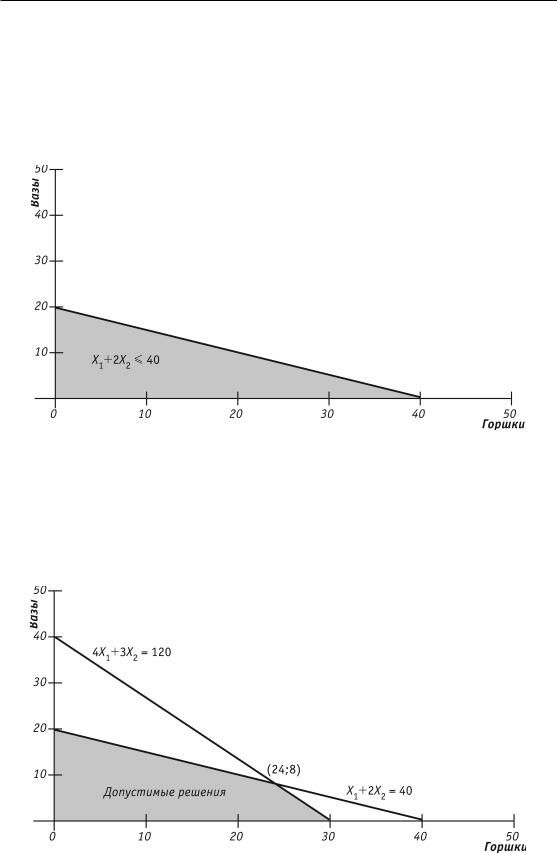
Раздел III. Технология принятия стратегических управленческих решений

ØÀà 6. ÏОСТРОЕНИЕ ЛИНИИ, ОТРАЖАЮЩЕЙ ПЕРВОЕ ОГРАНИ÷ÅÍÈÅ.

ОГРАНИчЕНИЕ ПО ТРУДУ ВЫРАЖАЕТСя НЕРАВЕНСТВОМ Õ1 + 2Õ2 ≤ 40. ÅÑËÈ Õ2 = 0, ÒÎ Õ1 ≤ 40, È Õ1 = 40 ДАЕТ ТОчКУ ПЕРЕСЕчЕНИя С ОСЬЮ X. ÅÑËÈ Õ1 = 0, ÒÎ Õ2 ≤ 20, È Õ2 = 20 ДАЕТ ТОчКУ ПЕРЕСЕчЕНИя С ОСЬЮ Y. ТОГДА ЛИНИя Õ1 + 2Õ2 = 40, ПРОВЕДЕННАя МЕЖДУ ДВУМя ЭТИМИ ТОчКАМИ ПЕРЕСЕчЕНИя, ДАСТ ВЕРХНЮЮ ГРАНИЦУ ЗАТЕНЕННОЙ ЗОНЫ, ПРЕДСТАВЛЕННОЙ НА РИС. 10.5. ВСЕ ТОчКИ, ЛЕЖАЩИЕ В ЭТОЙ ЗОНЕ, ВКЛЮчАя ТОчКИ НА ЭТОЙ ЛИНИИ, БУДУТ УДОВЛЕТВОРяТЬ ОГРАНИчЕНИЮ ПО ТРУДУ.

Ðèñ. 10.5. Ограничение по труду

ØÀà 7. ÏОСТРОЕНИЕ ЛИНИИ, ОТРАЖАЮЩЕЙ ВТОРОЕ ОГРАНИ÷ÅÍÈÅ.

ОГРАНИчЕНИЕ ПО МАТЕРИАЛАМ ВЫРАЖАЕТСя НЕРАВЕНСТВОМ 4Õ1 + 3Õ2 ≤ 120. ÅÑËÈ Õ2 = 0, ÒÎ Õ1 ≤ 30, È Õ1 = 30 ДАЕТ ТОчКУ ПЕРЕСЕчЕНИя С ОСЬЮ X. ÅÑËÈ Õ1 = 0, ÒÎ Õ2 ≤ 40, È Õ2 = 40 ДАЕТ ТОчКУ ПЕРЕСЕчЕНИя С ОСЬЮ Y. МЫ ПРОВОДИМ ЛИНИЮ 4Õ1 + 3Õ2 = 120 МЕЖДУ ЭТИМИ ТОчКАМИ ПЕРЕСЕчЕНИя (СМ. РИС. 10.6).

Ðèñ. 10.6. Область допустимых решений, удовлетворяющая всем ограничениям

221

Стратегический анализ

ПОСЛЕ ВЫПОЛНЕНИя ШАГА 7 ЛИНИя ОГРАНИчЕНИя ПО МАТЕРИАЛАМ ПЕРЕСЕКАЕТ ЛИНИЮ ОГРАНИчЕНИя ПО ТРУДУ В ТОчКЕ С КООРДИНАТАМИ (24; 8), КАК ЭТО ПОКАЗАНО НА РИС. 10.6. ЭТИ КООРДИНАТЫ МОЖНО НАЙТИ, РЕШИВ ОДНОВРЕМЕННО ОБА УРАВНЕНИя:

(X1 + 2X2 = 40) × 3 = 3X1 + 6X2 = 120; (4 X1 + 3X2 = 120) × 2 = 8 X1 + 6X2 = 240; −5 X1 = −120;

X1 = 24;

X1 + 2X2 = 40;

24 + 2X2 = 40;

2X2 = 16;

X2 = 8.

ЗАТЕНЕННАя ПЛОЩАДЬ НА РИС. 10.6 НАЗЫВАЕТСя ОБЛАСТЬЮ ДОПУСТИМЫХ РЕШЕНИЙ, ПОСКОЛЬКУ В НЕЙ СОДЕРЖАТСя ВСЕ СОчЕТАНИя ПЕРЕМЕННЫХ, УДОВЛЕТВОРяЮЩИЕ ВСЕМ ОГРАНИчЕНИяМ. ОчЕВИДНО, чТО СУЩЕСТВУЕТ ГРОМАДНОЕ КОЛИчЕСТВО ТАКИХ КОМБИНАЦИЙ: ФАКТИчЕСКИ ИХ чИСЛО БЕСКОНЕчНО, В СВяЗИ С чЕМ НЕТ НЕОБХОДИМОСТИ РАССМАТРИВАТЬ ЛЮБОЕ ИЗ ВОЗМОЖНЫХ СОчЕТАНИЙ ВНУТРИ ЗАТЕНЕННОЙ ОБЛАСТИ, ПОСКОЛЬКУ ОПТИМАЛЬНОЕ РЕШЕНИЕ НУЖНО ИСКАТЬ В ОДНОМ ИЗ УГЛОВ ИЛИ В КРАЙНИХ ТОчКАХ.

НА РИС. 10.7 ПРОИЛЛЮСТРИРОВАН БАЗОВЫЙ ПРИНЦИП РЕШЕНИя ЗАДАч ЛИНЕЙНОГО ПРОГРАММИРОВАНИя: ПРОВОДя ПАРАЛЛЕЛЬНЫЕ ЛИНИИ, ВЫРАЖАЮЩИЕ РАЗЛИчНЫЕ УРОВНИ ЦЕЛЕВОЙ ФУНКЦИИ Z = 4Õ1 + 5Õ2, МЫ ПОЛУчАЕМ РЕШЕНИя В УГЛУ ОБЛАСТИ ДОПУСТИМЫХ РЕШЕНИЙ.

Ðèñ. 10.7. Допустимые решения

222

Раздел III. Технология принятия стратегических управленческих решений

В НАчАЛЕ КООРДИНАТ (0; 0) ВСЕ ОГРАНИчЕНИя БУДУТ УДОВЛЕТВОРЕНЫ, НО ЗНАчЕНИЕ ЦЕЛЕВОЙ ФУНКЦИИ БУДЕТ РАВНО НУЛЮ. ПО МЕРЕ ПАРАЛЛЕЛЬНОГО ПЕРЕДВИЖЕНИя ЦЕЛЕВОЙ ФУНКЦИИ ОТ НАчАЛА КООРДИНАТ ПРИБЫЛИ УВЕЛИчИВАЮТСя. В ТОчКЕ (0; 20) ВСЕ ОГРАНИчЕНИя БУДУТ УДОВЛЕТВОРЕНЫ, А ПРИБЫЛЬ СОСТАВИТ 100 РУБ. ОНА МОЖЕТ БЫТЬ ПОВЫШЕНА ПРИ ПЕРЕХОДЕ К ТОчКЕ (30; 0). ЗДЕСЬ ВСЕ ОГРАНИчЕНИя ТАКЖЕ БУДУТ УДОВЛЕТВОРЕНЫ, А ПРИБЫЛЬ СОСТАВИТ 120 РУБ. ЭТО РЕШЕНИЕ ЕЩЕ НЕ БУДЕТ ОПТИМАЛЬНЫМ, ПОСКОЛЬКУ ПРИБЫЛЬ МОЖНО УВЕЛИчИТЬ, ЕСЛИ ПЕРЕЙТИ В ТОчКУ (24; 8), ГДЕ ПЕРЕСЕКАЮТСя ДВЕ ЛИНИИ ОГРАНИчЕНИЙ. ЗДЕСЬ ПРИБЫЛЬ СОСТАВИТ 136 РУБ. И БУДЕТ МАКСИМАЛЬНОЙ. ЕСЛИ МЫ УДАЛИМСя ОТ НАчАЛА КООРДИНАТ, ТО ОГРАНИчЕНИя БОЛЬШЕ НЕ БУДУТ УДОВЛЕТВОРяТЬСя, Т.Е. НИ ОДНА чАСТЬ ЛИНИИ ЦЕЛЕВОЙ ФУНКЦИИ НЕ БУДЕТ ЛЕЖАТЬ В ОБЛАСТИ ДОПУСТИМЫХ РЕШЕНИЙ. ЭТО ДЕМОНСТРИРУЕТ ЛИНИя 4Õ1 + 5Õ2 = 160.

Следует заметить, что задача линейного программирования необязательно имеет единственное решение. Если целевая функция будет параллельной одной из границ ограничений, то любая точка на этой границе будет оптимальной, давая бесконечное число решений. Другим предельным случаем может быть отсутствие решения задачи в сформулированном виде. Так, например, если задано минимальное количество единиц выпускаемой продукции, а ограничение по ресурсу таково, что его недостаточно для производства такого минимального количества, то задача не будет иметь решения. Симплексный метод, как будет показано далее, дает способ выявления задач,

не имеющих решения или имеющих бесконечное число решений. СИМПЛЕКСНЫЙ МЕТОД. Количественное решение задачи линейного

программирования симплексным методом вручную или на ЭВМ имеет два главных преимущества: 1) позволяет получить решение задачи с тремя и более переменными, ибо метод не ограничен трехмерным пространством; 2) значения дополнительных переменных в конечной форме уравнения дают чрезвычайно важную информацию для принятия решения.

Поскольку методика решения задачи не зависит от количества переменных в ней, для объяснения симплексного метода мы используем модель с двумя переменными, решенную ранее графиче- ски. Для этого мы внесем лишь небольшие изменения в постановку неотрицательных ограничений.

Цель: максимизировать Z = 4õ1 + 5õ2

при условии õ1 + 2õ2 ≤ 40; 4õ1 + 3õ2 ≤ 120;

õ1 + 0õ2 ≥ 0; 0õ1 + õ2 ≥ 0.

223

Стратегический анализ

Первый шаг в решении этой задачи состоит в том, чтобы преобразовать неравенства в уравнения. Эта трансформация достигается за счет введения дополнительных неотрицательных переменных, предназначенных единственно для того, чтобы покрыть различие между неравенством и уравнением, введя дополнение в неравенство. Если данное ограничение определяет верхний предел (знаком неравенства будет «≤»), то каждая такая дополнительная переменная

представляет собой количество располагаемого ресурса, которое не использовано и вводится с коэффициентом +1. Если такое ограни- чение определяет нижний предел (знаком неравенства будет «≥»), òî

каждая дополнительная переменная будет представлять величину, на которую использование располагаемого ресурса может превысить ограничение, и она вводится с коэффициентом −1. В нашем

примере нижний предел выражается исключительно неотрицательными ограничениями, соответственно введение дополнительных переменных дает следующую конструкцию:

Для решения задачи симплексным методом требуется канони- ческое построение матрицы дополнительных переменных n × n, ãäå n равно числу ограничений. Каноническое построение матрицы имеет место, когда каждое число главной диагонали матрицы n × n

равно +1. В нашем случае мы имеем для дополнительных переменных матрицу 4 × 4, но она не будет канонической, поскольку два ее

коэффициента будут отрицательными. Решение задачи состоит в том, чтобы каждому из таких уравнений добавить искусственную переменную с коэффициентом +1:

x1 + 2x2 + s1 = 40; 4x1 + 3x2 + s2 = 120; x1 + 0x2 − s3 + A1 = 0; 0x1 + x2 − s4 + A2 = 0.

Теперь мы имеем необходимое каноническое построение. Помимо матрицы ограничений искусственные переменные вводятся также в целевую функцию с очень большим коэффициентом Ì. Если мы максимизируем функцию, то этот большой коэффициент Ì

224

Раздел III. Технология принятия стратегических управленческих решений

берется со знаком «минус», если минимизируем, то со знаком «плюс». Так, модифицированная целевая функция приобретает вид

Z = 4x1 + 5x2 − MA1 − MA2.

Теперь мы имеем неопределенную систему из четырех уравнений с восьмью переменными: õ1, õ2, sl, s2, s3, s4, À1, A2. Расхождение

между числом переменных и числом уравнений делает их однознач- ное решение невозможным. Выполняемый вручную или с использованием ЭВМ симплексный метод дает решение задачи для n переменных, где n равно числу ограничений. Каждый раз набор этих пе-

ременных изменяется за счет замены одной переменной другой. Этот процесс называется итерацией. На каждой итерации мы полу-

чаем базисное допустимое решение, т.е. такое решение, которое удовлетворяет всем ограничениям и требованию, что число базисных переменных не должно превышать числа ограничений.

Симплексный метод изменяет базисные допустимые решения за счет ряда операций по строкам в табличном формате, называемом «табло». Для того чтобы начать решение симплексным методом, присвоим нулевое значение функциональным переменным, õi,

чтобы получить начальное базисное допустимое решение. Начальное табло (итерация 0) имеет вид, представленный в табл. 10.2.

ПОяСНЕНИЕ К НАчАЛЬНОМУ ТАБЛО. Вторая строка содержит заголовки столбцов, включающих все переменные задачи. Строка Cj содер-

жит коэффициенты переменных целевой функции. Они остаются постоянными во всех итерациях. Коэффициенты переменных ограничений показаны в ячейках матрицы n × m, ãäå n равно числу ограничений (четыре строки в нашем случае), а m равно общему числу

225

Стратегический анализ

переменных, включая функциональные переменные, дополнительные переменные и искусственные переменные (восемь столбцов в нашем случае). Каждую ячейку матрицы можно обозначить как aij, где индекс i относится к строке, а j указывает столбец. Правую границу матрицы составляет столбец, обозначенный как bi. Он содер-

жит правые части ограничений. Назначение столбца, обозначенного как bi/aie, будет пояснено далее.

Столбец «базис» показывает, какие базисные переменные входят в текущее базисное допустимое решение. Каждая базисная переменная в своем столбце будет иметь коэффициент 1. Слева от столбца «базис» находится столбец Ñb, куда введены коэффициенты

базисных переменных, входящих в целевую функцию. Дополнительные переменные входят в целевую функцию с нулевыми коэффициентами, искусственные переменные — с коэффициентами плюс или минус Ì в зависимости от того, будем ли мы максимизи-

ровать или минимизировать целевую функцию. В данном случае мы ее максимизируем, так что знаком будет минус.

Каждая ячейка строки Zi содержит изменения в целевой функ-

ции в результате ввода одной переменной, указанной в заголовке столбца. Таким образом,

n

Z j = ∑Cbaij .

i=1

Âначальном табло Z1 вычисляется как 0(1) + 0(4) + (−Ì)(1) +

+(−Ì)(0) = −Ì; Z2 вычисляется как 0(2) + 0(3) + (−M)(Î) + (−Ì)(1) = = −М. Остальные столбцы, включая столбец bi, вычисляются аналогично. Значение Z в столбце bi дает текущее значение целевой функ-

ции. В начальном табло это значение равно нулю, поскольку все функциональные переменные приравнены к нему.

Строка Cj − Zj содержит критерии оптимального решения. Если

мы максимизируем целевую функцию, то решение будет оптимальным, когда все Cj − Zj будут нулевыми или отрицательными, а если минимизируем, то решение будет оптимальным, когда все Cj − Zj áó-

дут нулевыми или положительными. В данном примере мы максимизируем функцию, и в строке Cj − Zj присутствуют два положи-

тельных элемента. Это означает, что мы не вышли на оптимум и по-

этому должны выбрать новый базис.

ВЫБОР НОВОГО БАЗИСА. Переход к новому базису осуществляется путем замены определенной базисной переменной некоторой небазисной, при этом одна переменная вводится в базис, а другая выводится из него. Сначала выбирается вводимая переменная, и это

226

Раздел III. Технология принятия стратегических управленческих решений

должна быть та, которая быстрее других наращивает значения Z. Ее определяет наибольшее положительное число в строке Cj − Zj. В нашем примере она будет находиться в столбце õ2, как это отмечено

вертикальной стрелкой в матрице, представленной в табл. 10.3. Величина, на которую может быть увеличена Z при введении

переменной, ограничена значением выводимой переменной, которая может быть уменьшена до нуля, но не может стать отрицательной. Предел приращения от вводимой переменной будет равен отношению bi к коэффициенту вводимой переменной, aje, где индекс å

указывает на столбец вводимой переменной. Это выражение называется min-отношением. Åñëè àiå равно нулю, то min-отношение будет стремиться к бесконечности. Если àiå отрицательно, то min-от-

ношение также будет отрицательным или нулевым, в зависимости от значения bi. В любом из этих случаев оно не определяет вводи-

мую переменную. Для каждой строки существует одно min-отноше- ние. Для данного примера min-отношение помещено в столбец b/àiå, как показано в матрице, представленной в табл. 10.3, однако

оно может не входить в распечатку, полученную в результате использования компьютерной программы.

Таблица 10.3

ВЫБОР ВВОДИМОЙ И ВЫВОДИМОЙ ПЕРЕМЕННЫХ

Выводимая переменная определяется наименьшей положительной величиной min-отношения. В нашем примере это будет À2, что показано горизонтальной стрелкой. Этот элемент, лежащий на пересечении столбца õ2 со строкой À2, называется ведущим, èëè íà-

правляющим, элементом. Поскольку мы хотим ввести переменную õ2 в базис, ведущий элемент должен измениться до 1. Это произво-

дится путем деления всех элементов строки на значение ведущего

227

Стратегический анализ

элемента. Все остальные элементы в столбце ведущего элемента должны быть приведены к нулю при помощи операций над строками, выполняемыми в следующем порядке.

В строке s1 значение коэффициента при õ2 равно 2. Для того чтобы изменить коэффициент на 0, мы умножаем новую строку õ2 íà 2

и полученное значение вычитаем из строки s1. Умножаем новую строку õ2 íà (−2) и складываем ее со строкой s1 (далее по аналогии).

Для строки s2 мы умножаем новую строку õ2 на 3 и вычитаем полученное значение из строки s2.

В строке À1 значение коэффициента при õ2 уже равно нулю, так

что нам нет необходимости вводить какие-либо изменения при решении задачи вручную. Компьютер, естественно, произведет умножение новой строки õ2 на 0 и вычтет полученное значение из строки À1.

Новое табло, полученное в результате таких операций над строками, показано в матрице, представленной в табл. 10.4. Это табло показывает, что значение Ñb для строки õ2 равняется 5. Это будет коэффициент при õ2 в целевой функции. Он используется для вы- числения новых значений строк Zj è Ñj - Zj. Столбец bi показывает, что Z остается равным нулю, что означает отсутствие увеличения целевой функции, однако строка Ñj − Zj теперь показывает, что ис-

кусственные переменные сводятся к нулю. Это позволяет эффективно удалить искусственные переменные из целевой функции, что желательно сделать как можно быстрее. По этой причине искусственным переменным дается значение Ì, ãäå Ì — очень большое число. Значение Ñj − Zj для второй искусственной переменной будет

сведено к нулю при следующей итерации.

Таблица 10.4

ТАБЛО ПОСЛЕ 1-Й ИТЕРАЦИИ

↑

228

Раздел III. Технология принятия стратегических управленческих решений

Вертикальная стрелка (↑) указывает на x1 как на вводимую пере-

менную для следующей итерации, поскольку она имеет наибольшее значение в строке Ñj − Zj. Вычислив min-отношения, получим вводимую переменную A1. После второй итерации получим матрицу,

представленную в табл. 10.5.

Таблица 10.5

ТАБЛО ПОСЛЕ 2-Й ИТЕРАЦИИ

↑

Для третьей итерации вводится s3 и выводится s1. Результат этой

итерации показан в матрице, представленной в табл. 10.6.

Таблица 10.6

ТАБЛО ПОСЛЕ 3-Й ИТЕРАЦИИ

↑

На следующей итерации вводится s4 и выводится s2. Ее результат

показан в матрице, представленной в табл. 10.7.

229

Стратегический анализ

Поскольку все переменные в строке Cj − Zj будут нулевыми или

отрицательными, это означает, что получено оптимальное решение при значении Z, равном 136. Значения базисных переменных в оптимальном решении можно найти в столбце bi. Значения остальных

небазисных переменных в оптимальном решении будут равны нулю. Соответственно решением будет [x1, õ2, s1, s2, s3, s4, A1, A2] =

[24, 8, 0, 0, 8, 24, 0, 0]. Из этого следует, что все имеющиеся в нали- чии ресурсы труда и глины будут израсходованы для производства 24 горшков и 8 ваз и принесут общую прибыль в 136 руб.

При решении задач симплексным методом могут возникнуть

определенные трудности.

МИНИМИЗАЦИя. Минимизация целевой функции эквивалентна максимизации ее отрицательных значений. Например, минимиза-

бой из них может быть введен в компьютерную программу. Для этого необходимо:

1. Преобразовать критерии оптимальности с тем, чтобы выбрать переменные, имеющие наибольшие отрицательные значения Cj − Zj

в качестве вводимых переменных, и закончить их ввод, когда все значения Cj − Zj будут равны нулю или будут положительными. Зна- чения Cj − Zj наибольшие по модулю отрицательные значения, т.к.

лишь в этом случае выбирается переменная, которая быстрее других уменьшает целевую функцию. В случае выбора наибольшего отрицательного значения результат будет противоположным.

2. Изменить целевую функцию с Z íà Z ′, т.е. обратить знак при Cj на противоположный, и вести их расчет в обычном порядке.

230