7.4. Линейная модель парной регрессии. Оценка значимости параметров линейной регрессии

Рассмотрим простейшую линейную модель. Предположим, что имеется выборка n-значений двух переменных: - объясняемая переменная и- объясняющая переменная. Если между переменнымиY и X теоретически существует некоторая линейная зависимость, то ее можно описать в виде уравнения регрессии

. (7.2)

Задача заключается в определении параметров α и β. Уравнение (7.2) будем называть «истинным» уравнением регрессии. В действительности между переменными Y и X наблюдается не столь жесткая линейная связь. Отдельные наблюдения y будут отклоняться от линейной зависимости в силу воздействия различных причин. Обычно зависимая переменная находится под влиянием целого ряда факторов, в том числе и неизвестных исследователю, а также случайных причин (возмущения и помехи). Существенным источником отклонений в ряде случаев являются ошибки измерения. Отклонения от предполагаемой формы связи могут возникнуть и в силу неправильного выбора вида уравнения, описывающего эту зависимость. В дальнейшем будем полагать, что спецификация модели выполнена правильно. Учитывая возможные отклонения, линейное уравнение связи двух переменных (парную регрессию) представим в виде:

, (7.3)

где α - постоянная величина (или свободный член уравнения);

β – коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдения;

- случайная переменная, характеризующая отклонение от теоретически предполагаемой регрессии (случайная составляющая, остаток, возмущение).

Коэффициент регрессии β характеризует изменение переменной при изменении значенияна единицу. Еслиβ>0, связь между переменными ипрямая, если β <0 , то связь обратная.

Случайная составляющая отражает тот факт, что изменениебудет неточно описываться изменением, так как присутствуют другие факторы, неучтенные в данной модели.

Таким образом, в уравнении (7.3) значение каждого наблюдения представлено как сумма двух частей – систематическойи случайной. В свою очередь, систематическую часть можно представить в виде уравнения

, (7.4)

где характеризует некоторое среднее значениедля данного значенияx. Соответственно уравнение (7.3) показывает значения с учетом возможных отклонений от средних значений.

Основные предпосылки метода наименьших квадратов

Для классической (традиционной) линейной регрессионной модели должны выполняться следующие условия, известные как условия Гаусса-Маркова:

1. Математическое ожидание случайной составляющей в любом наблюдении должно быть равно нулю: 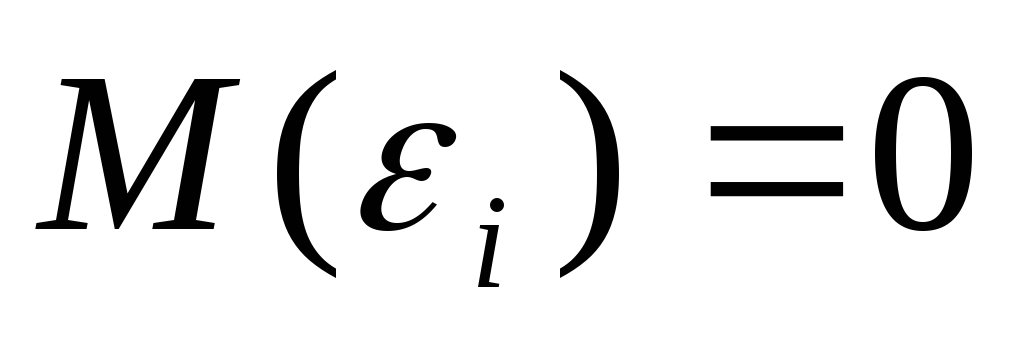. Иногда случайная составляющая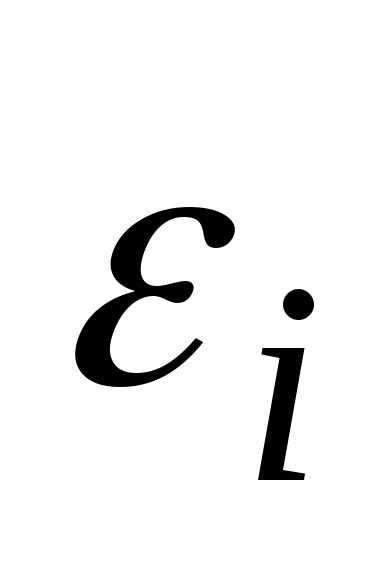будет положительной, иногда отрицательной, но она не должна иметь систематического смещения ни в одном из двух возможных направлений. Фактически если уравнение регрессии включает постоянный член, то обычно данное условие выполняется автоматически, так как роль константы состоит в определении любой систематической тенденции вY, которую не учитывают объясняющие переменные, включенные в уравнение регрессии.

2. Дисперсия случайного члена должна быть постоянна для всех наблюдений: 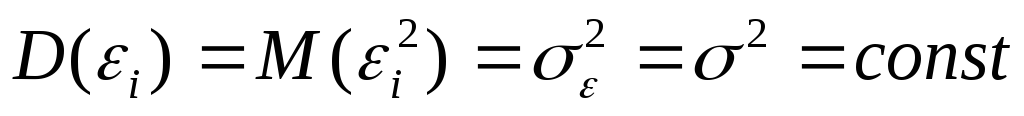. Иногда случайный член будет больше, иногда меньше, однако не должно быть априорной причины для того, чтобы он порождал большую ошибку в одних наблюдениях, чем в других. Величинаσ_ε, конечно, неизвестна, одна из задач регрессионного анализа состоит в оценке стандартного отклонения случайной составляющей.

3. В любых двух наблюдениях отсутствует систематическая связь между значениями случайной составляющей: 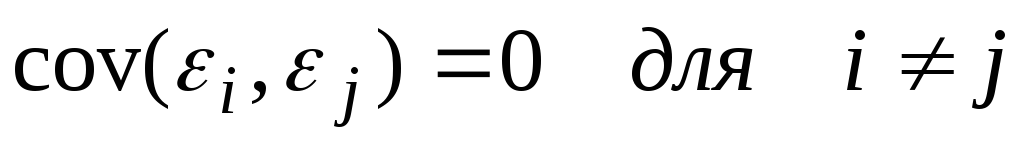. Если случайная составляющая велика и положительна в одном наблюдении, то это не должно обуславливать систематическую тенденцию к тому, что она будет большой и положительной в следующем наблюдении. Случайные составляющие должны быть независимы друг от друга. В силу того, что 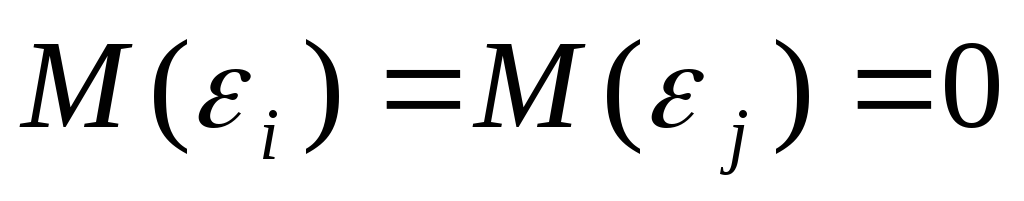, данное условие можно записать следующим образом:.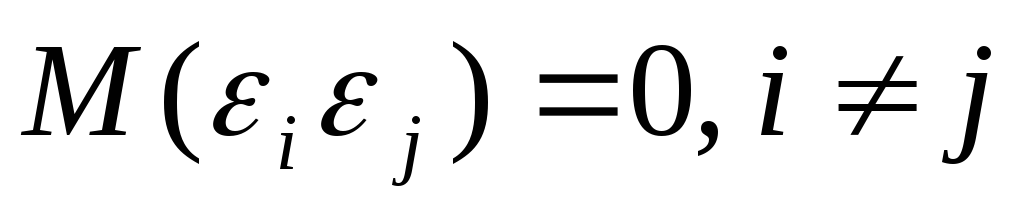

4. Случайная составляющая должна быть распределена независимо от объясняющих переменных. В сущности используется более сильное предположение о том, что объясняющие переменные не являются стохастическими, т.е. не имеют случайной составляющей. Значение любой независимой переменной в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии. Ели это условие выполнено, то теоретическая ковариация между независимой переменной и случайным членом равна нулю:

Наряду с условиями Гаусса-Маркова обычно предполагается нормальность распределения случайного члена: ~. Дело в том, что если случайный член нормально распределен, то так же будут распределены и коэффициенты регрессии.

Предположение о нормальности основывается на центральной предельной теореме, которая утверждает, что если случайная величина является общим результатом взаимодействия большого числа случайных величин, ни одна из которых не является доминирующей, то она будет иметь приблизительно нормальное распределение, даже если отдельные составляющие не имеют нормального распределения. Случайный член определяется несколькими факторами, которые не входят в уравнение регрессии. Поэтому даже если ничего не известно о распределении этих факторов (или даже об их сущности), можно предположить, что они нормально распределены.

Свойства оценок параметров, получаемых МНК

Определение параметров уравнения регрессии α и β проводится по выборке ограниченного характера, поэтому истинные значения параметров получить нельзя. Найденные значения параметров являются статистическими оценками истинных (неизвестных) параметров. Обозначим соответствующие оценки через a и b. Таким образом, оценкой модели является уравнение парной регрессии.

В случае, когда условия, высказанные относительно случайной составляющей выполняются, оценки, полученные методом наименьших квадратов, будут обладать свойствами несмещенности, эффективности и состоятельности.

Оценки параметров являются несмещенными, если математическое ожидание оценки равно истинному значению параметра. Для модели парной регрессии и. Несмещенность оценок означает, что выборочные оценки параметров концентрируются вокруг истинных неизвестных значений параметров.

Оценки являются эффективными, если они имеют минимальную дисперсию по сравнению с другими несмещенными оценками этого параметра.

Оценки параметров состоятельны, если дисперсия оценки параметра стремится к нулю с возрастанием объема выборки n. Свойство состоятельности означает, что с увеличением объема выборки оценки параметров становятся более надежными в вероятностном смысле, т.е. с увеличением n оценки плотнее концентрируются вокруг истинных неизвестных значений параметров.

Если предположения 2 и 3 относительно случайной составляющей невыполняются, то оценки коэффициентов регрессии, найденные по обычному методу наименьших квадратов, будут неэффективными, свойство несмещенности оценок сохраняется.

МНК для модели парной регрессии

Наиболее часто оценку параметров уравнения регрессии осуществляют на основе метода наименьших квадратов (МНК). Согласно МНК для оценки параметров регрессионного уравнения используется следующий критерий:

сумма квадратов отклонений наблюдаемых значений результативного признака от расчетных (теоретических) значений должна быть минимальной:

.

Для модели линейной парной регрессии это условие запишется как:

.

Исходными данными для оценки параметров a и b являются наблюдаемые значения зависимой переменной и независимых переменных. В функцииS они представляют собой константы. Переменными в этой функции являются оценки параметров a и b. Необходимым условием существования минимума функции является равенство нулю частных производных по неизвестным параметрам a и b:

, .

Согласно правилам вычисления производных:

,

.

Оптимальные по данному критерию значения оценок в этом случае могут быть найдены решением системы нормальных уравнений, вытекающей из условия равенства нулю частных производных функции S по своим параметрам в точке минимума:

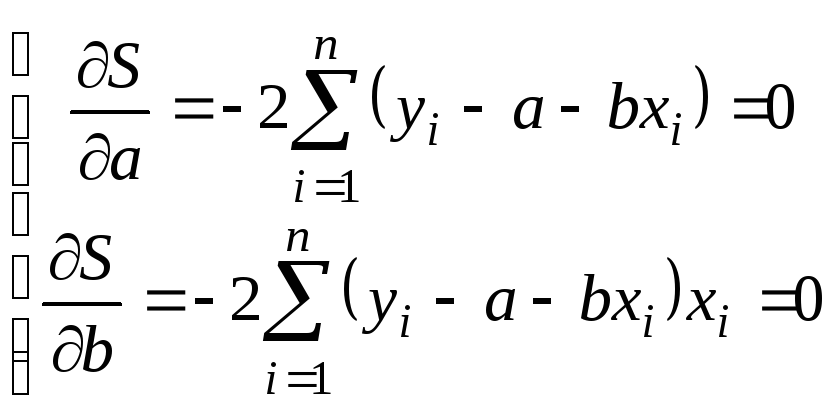или

.

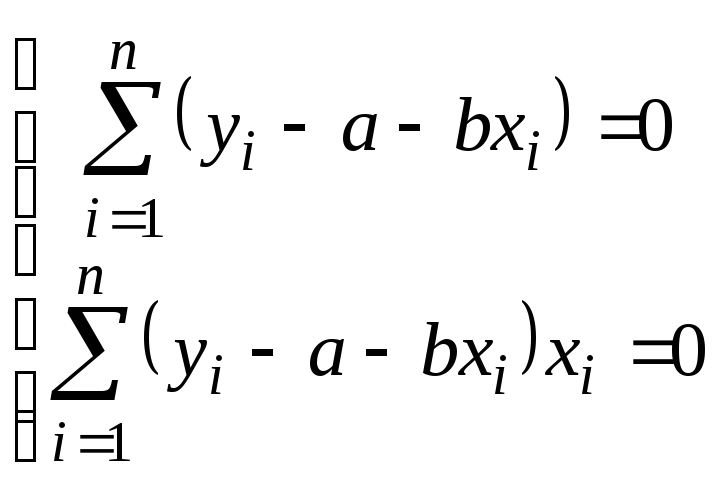Раскрыв скобки, получим стандартную форму нормальных уравнений:

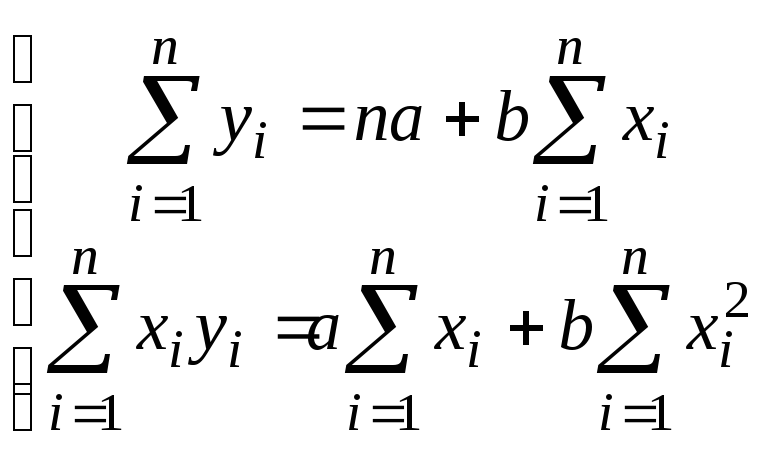
Решая данную систему, найдем искомые оценки параметров уравнения регрессии:

,

.

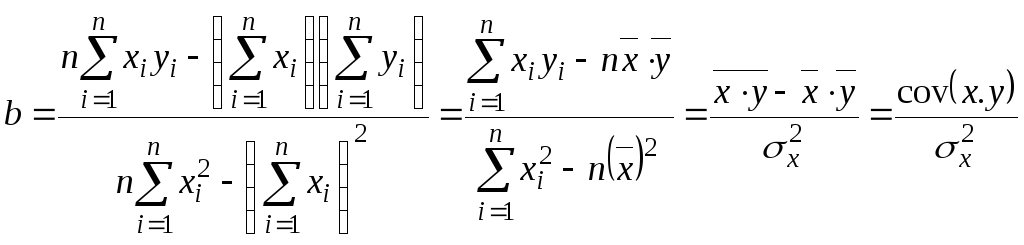Таким образом, МНК дает такие оценки a и b, что найденная прямая проходит через точку с координатами . Если начало координат переместить в точку, то система нормальных уравнений упростится и параметрb можно получить следующим образом:

.

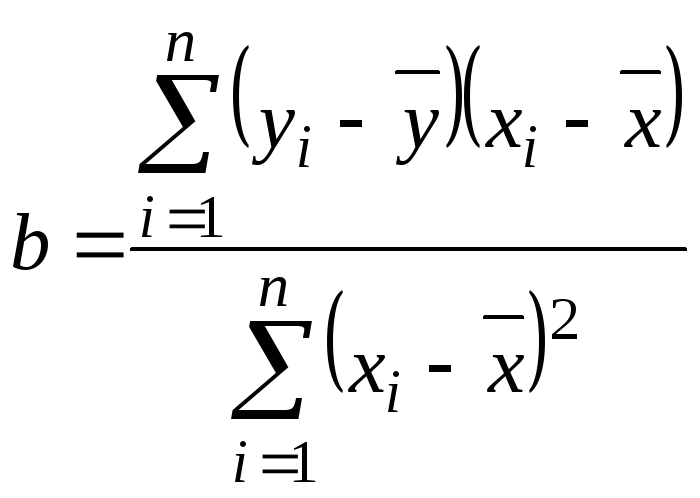Такое решение может существовать только при выполнении условия

, (7.5)

что равносильно отличию от нуля определителя системы нормальных уравнений. Условие (7.5) называется условием идентифицируемости модели наблюдений , и означает, что не все значениясовпадают между собой. При нарушении этого условия все точки лежат на одной вертикальной прямой.

Матричная форма записи модели парной регрессии

Матричная форма записи модели парной регрессии имеет вид:

,

где Y – вектор-столбец размерности nх1 наблюдаемых значений зависимой переменной;

X – матрица размерности nх2 наблюдаемых значений факторных признаков (дополнительно вводится фактор, состоящий из одних единиц для вычисления свободного члена);

а – вектор-столбец размерности 2х1 неизвестных, подлежащих оценке коэффициентов регрессии;

ε – вектор-столбец размерности n.

Таким образом,

,,,.

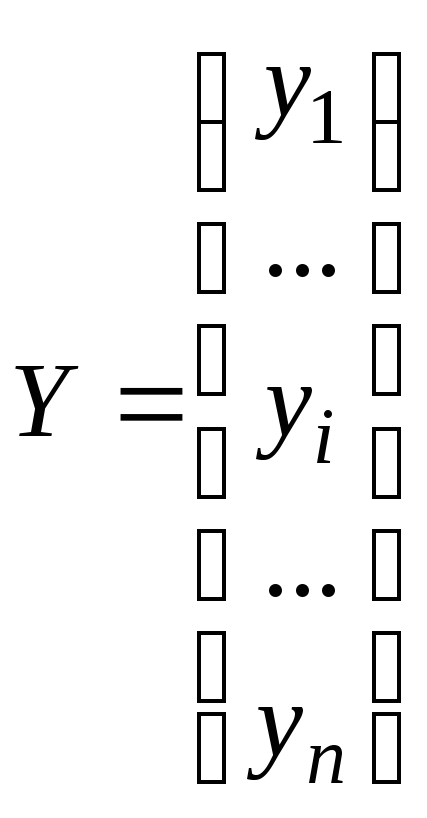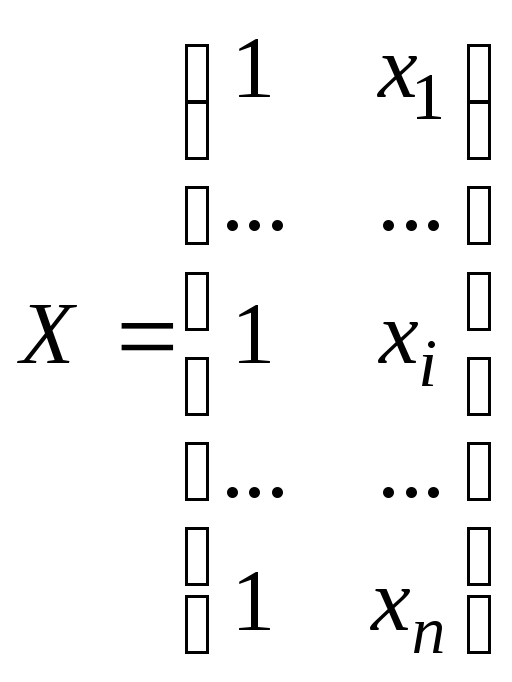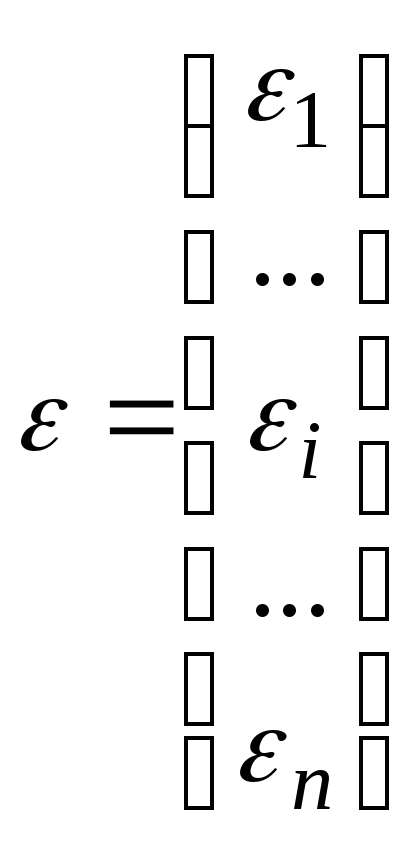В матричной форме критерий МНК записывается следующим образом:

,

где индекс Т означает транспонирование.

Чтобы найти оценки вектора а методом наименьших квадратов, продифференцируем S по вектору а и приравняем производные нулю:

или

.

Откуда следует, что вектор а определяется на основе матричного выражения:

,

где индекс -1 означает обратную матрицу.

Оценка значимости уравнения регрессии в целом и его параметров

Оценив параметры a и b, мы получили уравнение регрессии, по которому можно оценить значения y по заданным значениям x. Естественно полагать, что расчетные значения зависимой переменной не будут совпадать с действительными значениями, так как линия регрессии описывает взаимосвязь лишь в среднем, в общем. Отдельные значения рассеяны вокруг нее. Таким образом, надежность получаемых по уравнению регрессии расчетных значений во многом определяется рассеянием наблюдаемых значений вокруг линии регрессии. На практике, как правило, дисперсия ошибок неизвестна и оценивается по наблюдениям одновременно с параметрами регрессии a и b. Вполне логично предположить, что оценка связана с суммой квадратов остатков регрессии. Величина является выборочной оценкой дисперсии возмущений, содержащихся в теоретической модели. Можно показать, что для модели парной регрессии

,

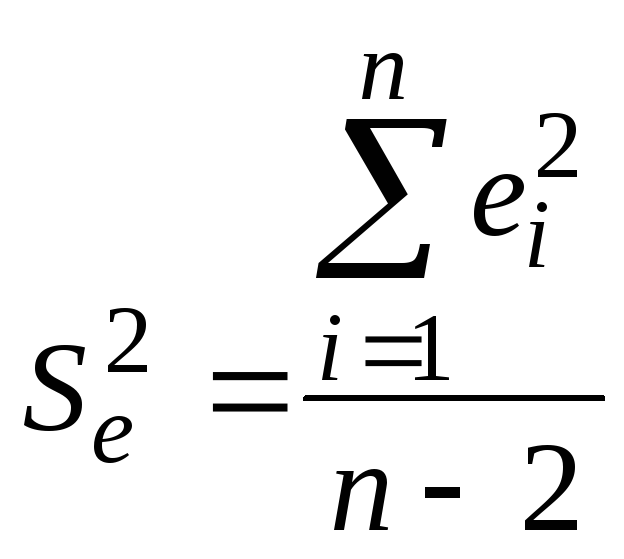где - отклонение фактического значения зависимой переменной от ее расчетного значения.

Если , то для всех наблюдений фактические значения зависимой переменной совпадают с расчетными (теоретическими) значениями. Графически это означает, что теоретическая линия регрессии (линия, построенная по функции )проходит через все точки корреляционного поля, что возможно только при строго функциональной связи. Следовательно, результативный признак у полностью обусловлен влиянием фактора х.

Обычно на практике имеет место некоторое рассеивание точек корреляционного поля относительно теоретической линии регрессии, т. е. отклонения эмпирических данных от теоретических . Этот разброс обусловлен как влиянием факторах, т.е. регрессией y по х, (такую дисперсию называют объясненной, так как она объясняется уравнением регрессии), так и действием прочих причин (необъясненная вариация, случайная). Величина этих отклонений и лежит в основе расчета показателей качества уравнения.

Согласно основному положению дисперсионного анализа общая сумма квадратов отклонений зависимой переменной y от среднего значения может быть разложена на две составляющие: объясненную уравнением регрессии и необъясненную:

,

где - значенияy, вычисленные по уравнению .

Найдем отношение суммы квадратов отклонений, объясненной уравнением регрессии, к общей сумме квадратов:

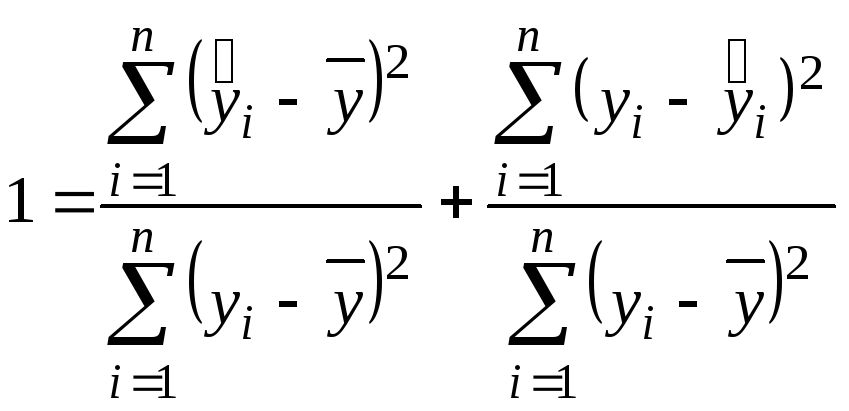, откуда

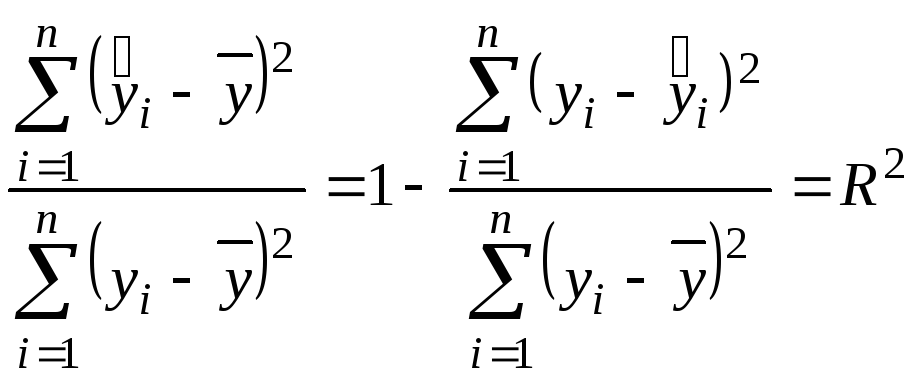. (7.6)

Отношение части дисперсии, объясненной уравнением регрессии к общей дисперсии результативного признака называется коэффициентом детерминации . Значениене может превзойти единицы и это максимальное значение будет только достигнуто при, т.е. когда каждое отклонениеравно нулю и поэтому все точки диаграммы рассеяния в точности лежат на прямой.

Коэффициент детерминации характеризует долю объясненной регрессией дисперсии в общей величине дисперсии зависимой переменной. Соответственно величина характеризует долю вариации (дисперсии) у, необъясненную уравнением регрессии, а значит, вызванную влиянием прочих неучтенных в модели факторов. Чем ближе к единице, тем выше качество модели.

При парной линейной регрессии коэффициент детерминации равен квадрату парного линейного коэффициента корреляции: .

Корень из этого коэффициента детерминации есть коэффициент (индекс) множественной корреляции, или теоретическое корреляционное отношение.

Для того чтобы узнать, действительно ли полученное при оценке регрессии значение коэффициента детерминации отражает истинную зависимость между y и x выполняют проверку значимости построенного уравнения в целом и отдельных параметров. Проверка значимости уравнения регрессии позволяет узнать, пригодно уравнение регрессии для практического использования, например, для прогноза или нет.

При этом выдвигают основную гипотезу о незначимости уравнения в целом, которая формально сводится к гипотезе о равенстве нулю параметров регрессии, или, что то же самое, о равенстве нулю коэффициента детерминации: . Альтернативная гипотеза о значимости уравнения — гипотеза о неравенстве нулю параметров регрессии или о неравенстве нулю коэффициента детерминации: .

Для проверки значимости модели регрессии используют F-критерий Фишера, вычисляемый как отношение суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы):

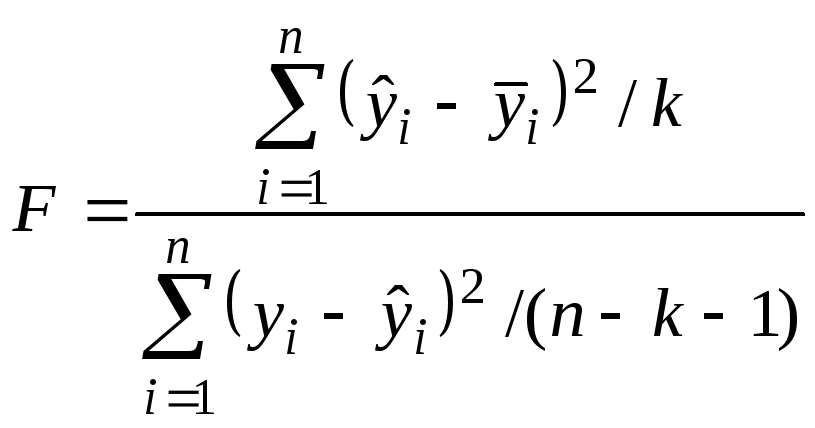, (7.7)

где k – число независимых переменных.

После деления числителя и знаменателя соотношения (7.7) на общую сумму квадратов отклонений зависимой переменной, F-критерий может быть эквивалентно выражен на основе коэффициента :

.

Если нулевая гипотеза справедлива, то объясненная уравнением регрессии и необъясненная (остаточная) дисперсии не отличаются друг от друга.

Расчетное значение F-критерий сравнивается с критическим значением, которое зависит от числа независимых переменных k, и от числа степеней свободы (n-k-1). Табличное (критическое) значение F-критерия – это максимальная величина отношений дисперсий, которое может иметь место при случайном расхождении их для заданного уровня вероятности наличия нулевой гипотезы. Если расчетное значение F-критерий больше табличного при заданном уровне значимости, то нулевая гипотеза об отсутствии связи отклоняется и делается вывод о существенности этой связи, т.е. модель считается значимой.

Для модели парной регрессии

.

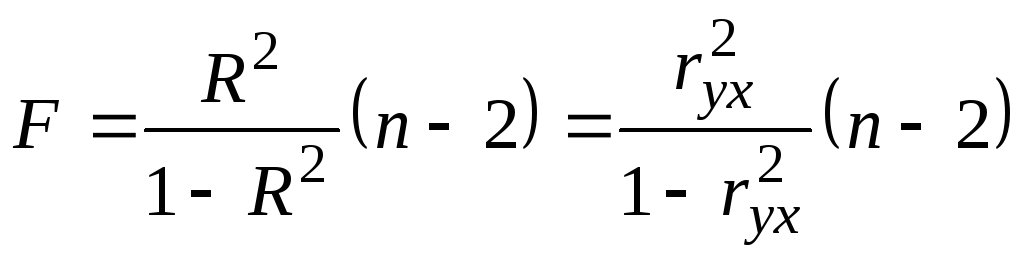В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его коэффициентов. Для этого определяется стандартная ошибка каждого из параметров. Стандартные ошибки коэффициентов регрессии параметров определяются по формулам:

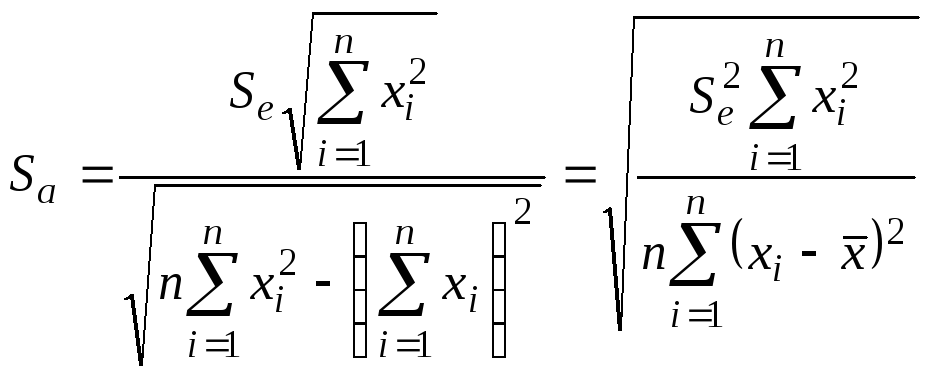, (7.8)

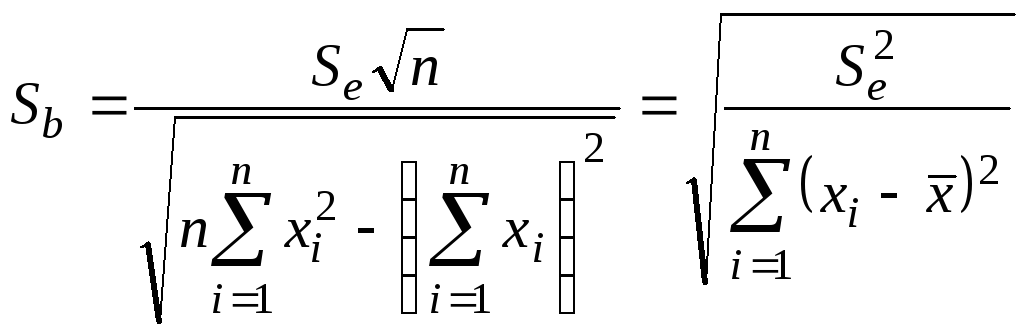(7.9)

Стандартные ошибки коэффициентов регрессии или среднеквадратические отклонения, рассчитанные по формулам (7.8,7.9), как правило, приводятся в результатах расчета модели регрессии в статистических пакетах.

Опираясь на среднеквадратические ошибки коэффициентов регрессии, проверяют значимость этих коэффициентов используя обычную схему проверки статистических гипотез.

В качестве основной гипотезы выдвигают гипотезу о незначимом отличии от нуля «истинного» коэффициента регрессии. Альтернативной гипотезой при этом является гипотеза обратная, т. е. о неравенстве нулю «истинного» параметра регрессии. Проверка этой гипотезы осуществляется с помощью t-статистики, имеющей t-распределение Стьюдента:

, .

Затем расчетные значения t-статистики сравниваются с критическими значениями t-статистики, определяемыми по таблицам распределения Стьюдента. Критическое значение определяется в зависимости от уровня значимости α и числа степеней свободы, которое равно (n-k-1), п — число наблюдений, k - число независимых переменных. В случае линейной парной регрессии число степеней свободы равно (п-2). Критическое значение также может быть вычислено на компьютере с помощью встроенной функции СТЬЮДРАСПОБР пакета Ехсеl.

Если расчетное значение t-статистики больше критического, то основную гипотезу отвергают и считают, что с вероятностью (1-α) «истинный» коэффициент регрессии значимо отличается от нуля, что является статистическим подтверждением существования линейной зависимости соответствующих переменных.

Если расчетное значение t-статистики меньше критического, то нет оснований отвергать основную гипотезу, т. е. «истинный» коэффициент регрессии незначимо отличается от нуля при уровне значимости α. В этом случае фактор, соответствующий этому коэффициенту должен быть исключен из модели.

Значимость коэффициента регрессии можно установить методом построения доверительного интервала. Доверительный интервал для параметров регрессии a и b определяют следующим образом:

,

,

где определяется по таблице распределения Стьюдента для уровня значимостиα и числа степеней свободы (п-2) для парной регрессии.

Поскольку коэффициенты регрессии в эконометрических исследованиях имеют четкую экономическую интерпретацию, доверительные интервалы не должны содержать нуль. Истинное значение коэффициента регрессии не может одновременно содержать положительные и отрицательные величины, в том числе и нуль, иначе мы получаем противоречивые результаты при экономической интерпретации коэффициентов, чего не может быть. Таким образом, коэффициент значим, если полученный доверительный интервал не накрывает нуль.

Пример 7.4. По данным примера 7.1:

а) Построить парную линейную модель регрессии зависимости прибыли от реализации от отпускной цены с использованием программных средств обработки данных.

б) Оценить значимость уравнения регрессии в целом, используя F-критерий Фишера при α=0,05.

в) Оценить значимость коэффициентов модели регрессии, используя t-критерий Стьюдента при α=0,05 и α=0,1.

Для проведения регрессионного анализа используем стандартную офисную программу EXCEL. Построение регрессионной модели проведем с помощью инструмента РЕГРЕССИЯ настройки ПАКЕТ АНАЛИЗА (рис.7.5), запуск которого осуществляется следующим образом:

СервисАнализ данныхРЕГРЕССИЯОК.

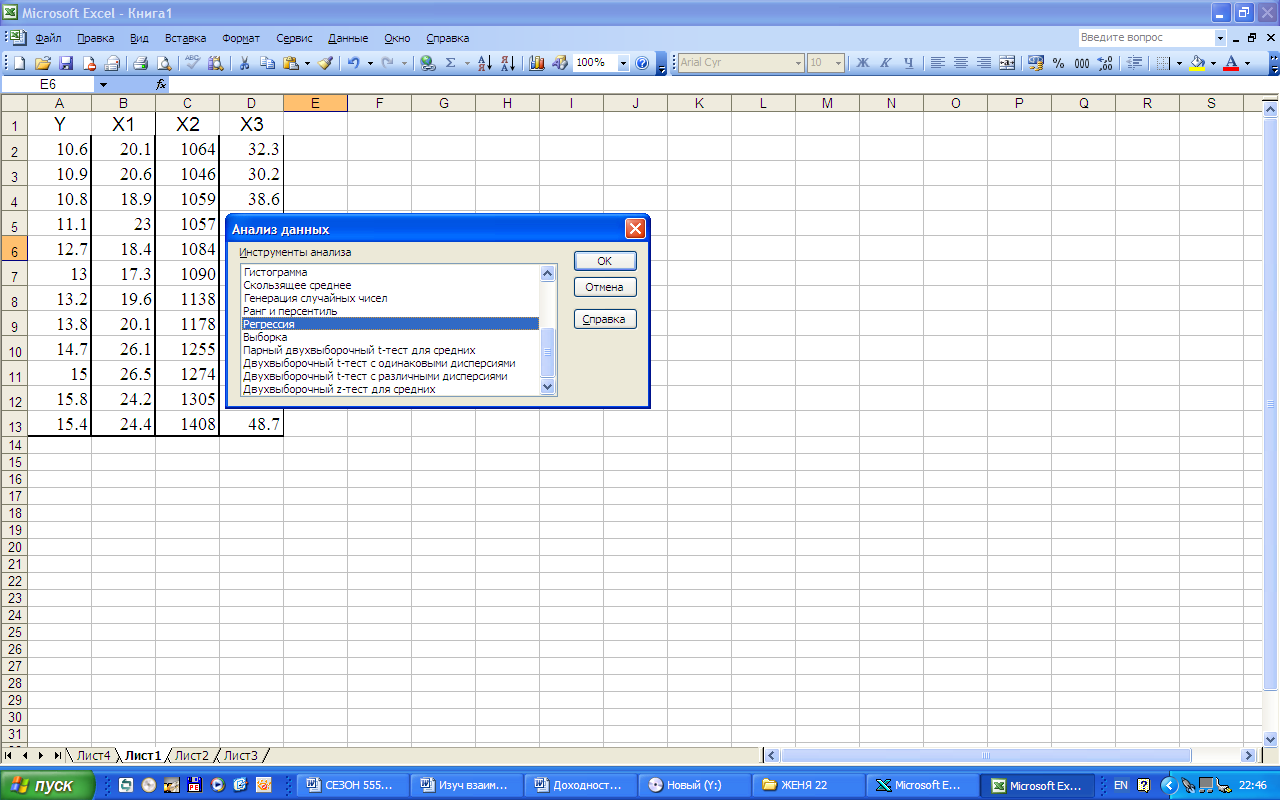
Рис.7.5. Использование инструмента РЕГРЕССИЯ

В диалоговом окне РЕГРЕССИЯ в поле Входной интервал Y необходимо ввести адрес диапазона ячеек, содержащих зависимую переменную. В поле Входной интервал Х нужно ввести адреса одного или нескольких диапазонов, содержащих значения независимых переменных Флажок Метки в первой строке – устанавливается в активное состояние, если выделены и заголовки столбцов. На рис. 7.6. показана экранная форма вычисления модели регрессии с помощью инструмента РЕГРЕССИЯ.

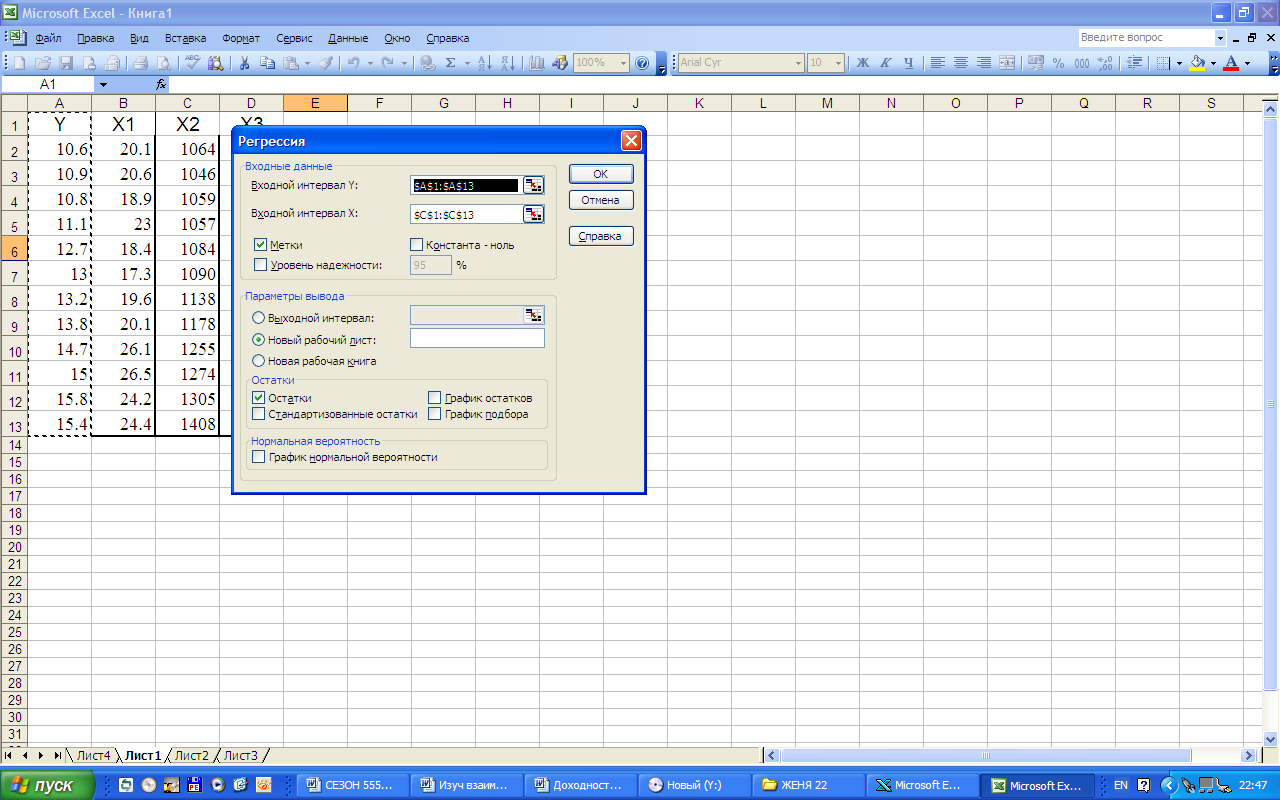
Рис. 7.6. Построение модели парной регрессии с помощью

инструмента РЕГРЕССИЯ

В результате работы инструмента РЕГРЕСИЯ формируется следующий протокол регрессионного анализа (рис.7.7).

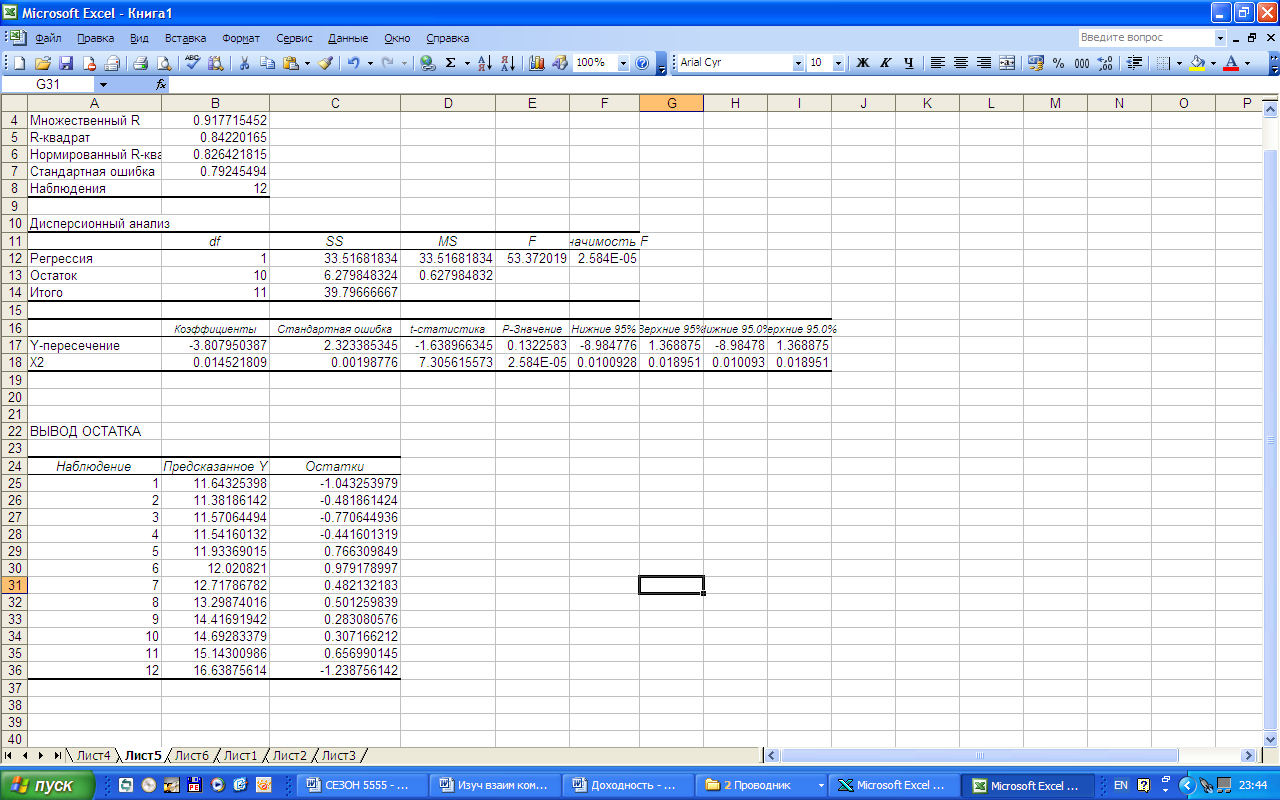
Рис. 7.7. Протокол регрессионного анализа

Уравнение зависимости прибыли от реализации от отпускной цены имеет вид:

.

Оценку значимости уравнения регрессии проведем используя F-критерий Фишера. Значение F-критерий Фишера возьмем из таблицы «Дисперсионный анализ» протокола EXCEL (рис. 7.7.). Расчетное значение F-критерия 53,372. Табличное значение F-критерия при уровне значимости α=0,05 и числе степеней свободы составляет 4,964. Так как, то уравнение считается значимым.

Расчетные значения t-критерия Стьюдента для коэффициентов уравнения регрессии приведены в результативной таблице (рис. 7.7). Табличное значение t-критерия Стьюдента при уровне значимости α=0,05 и 10 степенях свободы составляет 2,228. Для коэффициента регрессии a , следовательно коэффициентa не значим. Для коэффициента регрессии b , следовательно, коэффициентb значим.