Упорядоченность поля рациональных чисел.

Определение. Поле 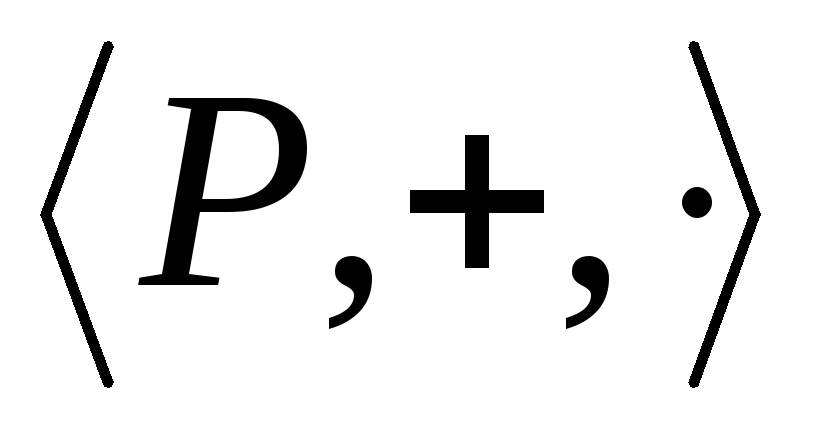называется упорядоченным, если кольцо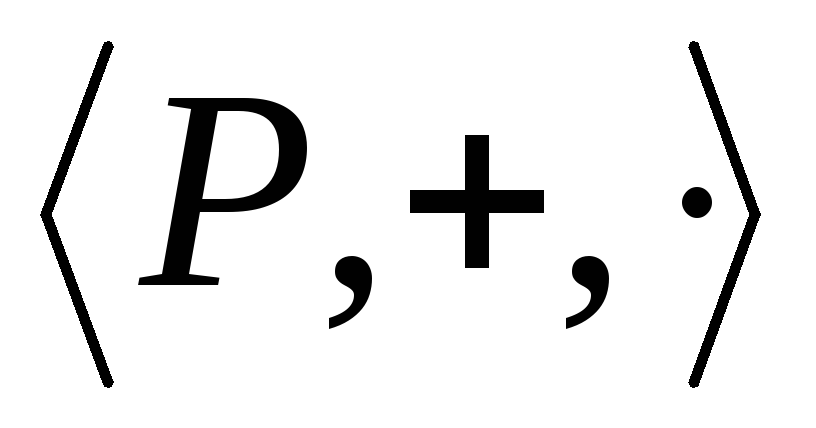является упорядоченным.

Теорема 5. Поле рациональных чисел упорядоченное.

Доказательство.

Рассмотрим подмножество . Легко проверить аксиомы положительного конуса.

возможен один из трех случаев:

• ,

• 

• .

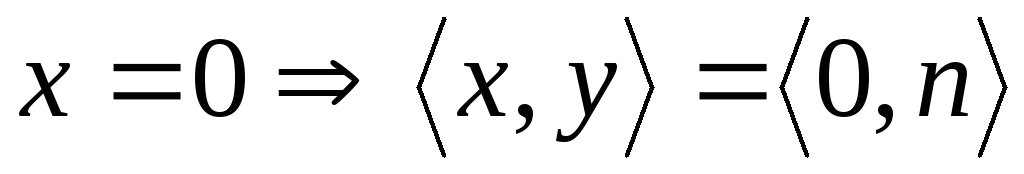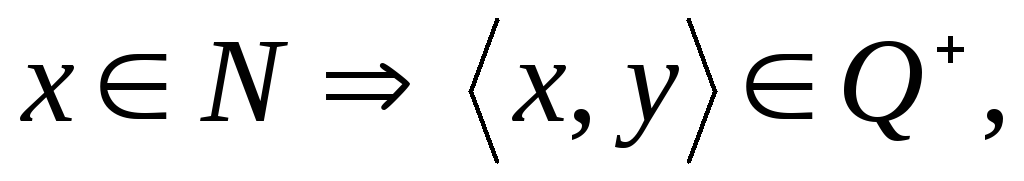
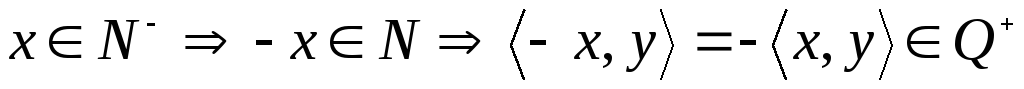что и требовалось доказать.

Следствие 1. Бинарное отношение < на Q, определенное по правилу является строгим линейным порядком и удовлетворяет свойствам 1.-6. (см. теорему об упорядоченных кольцах).

Следствие 2. Бинарное отношение наQ, определенное по правилу является линейным порядком.

Архимедовская расположенность поля рациональных чисел.

Теорема 6. Поле рациональных чисел архимедовски расположенное, т.е. выполняется аксиома Архимеда: .

Доказательство.

Пусть .

Заметим, что .

Поскольку кольцо целых чисел является архимедовски расположенным, имеем:

что и требовалось доказать.

Теорема 7. Поле рациональных чисел является всюду плотным.

Доказательство.

Пусть . Для определенности положим, что. Покажем, что элементлежит между указанными элементами, т.е.. Докажем каждое из неравенств отдельно.

(?)

(?)

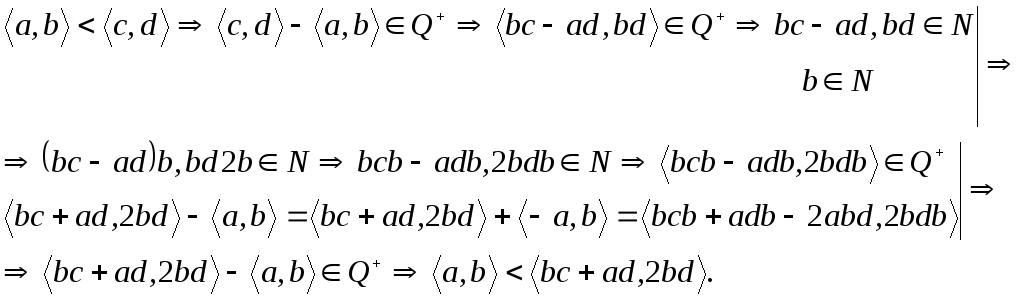
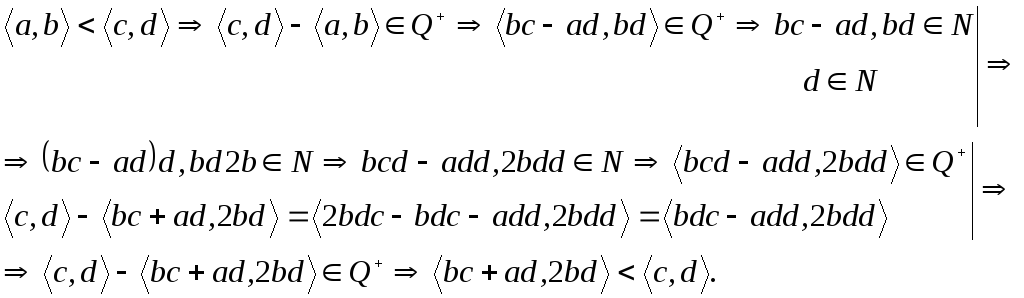
что и требовалось доказать.

Лекция 7. Фундаментальные последовательности рациональных чисел и их свойства

Определение. Последовательностью рациональных чисел называется всякое отображение .

–ый член этой последовательности.

Определение. Последовательность рациональных чисел называется сходящейся в полеQ к числу в том и только том случае, когдаЧислоназывается пределом данной последовательности. Обозначать этот факт будемприили.

Определение. Последовательность называется фундаментальной последовательностью рациональных чисел (ф.п.р.ч.) в том и только том случае, когда.

Свойство 1 ф.п.р.ч. Любая сходящаяся в поле рациональных чисел последовательность является фундаментальной последовательностью рациональных чисел.свойства

Доказательство.

Пусть сходится кb. Тогда

.

Оценим :

.

В силу произвольности также произвольно, следовательно, фундаментальность доказана.

что и требовалось доказать.

Определение. Подпоследовательностью последовательности называется последовательностьтакая, что, причем отображениеявляется монотонно возрастающей функцией для каждого натурального.

Теорема 1. Любая подпоследовательность сходящейся последовательности рациональных чисел является сходящейся к тому же числу последовательностью рациональных чисел.

Доказательство.

Пусть подпоследовательность последовательности, где. Возьмем произвольное рациональное число, тогда в силу сходимости найдется такое, что. Пустьk – произвольное натуральное число, большее . Тогда т.к. . Следовательно, последовательностьсходится кA.

что и требовалось доказать.

Свойство 2 ф.п.р.ч. Любая подпоследовательность фундаментальной последовательности рациональных чисел является фундаментальной последовательностью рациональных чисел.

Доказательство.

Пусть подпоследовательность последовательности, где. Возьмем произвольное рациональное число, тогда в силу сходимости найдется такое, что. Пустьk – произвольное натуральное число, большее . Тогда т.к. . Следовательно, последовательностьсходится кA.

Докажем фундаментальность подпоследовательности фундаментальной последовательности. Из того, что- ф.п.р.ч. следует, что. Пустьx, y – произвольные натуральные числа, большие . Оценим:

.

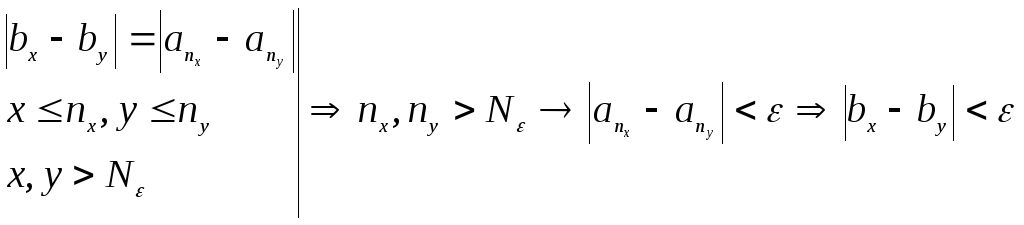Таким образом, фундаментальность доказана.

что и требовалось доказать.

Замечание. Любая постоянная последовательность является фундаментальной (в силу ее сходимости).

Определение. Последовательность рациональных чисел называется ограниченной рациональным числомв том и только том случае, когда.

Свойство 3 ф.п.р.ч. Любая фундаментальная последовательность рациональных чисел является ограниченной.

Доказательство.

Пусть - ф.п.р.ч. Тогда. Возьмем. Зная, что. Поскольку последнее неравенство выполняется для любых, в том числе и для. Следовательно,. Мы нашли число, ограничивающее все члены последовательностипо абсолютной величине, начиная с номера. Тогда, полагая, получим.

что и требовалось доказать.