
- •Федеральное агентство по образованию
- •Независимость аксиом Пеано.
- •Непротиворечивость системы аксиом Пеано.
- •Категоричность теории натуральных чисел.
- •Сложение натуральных чисел.
- •Свойства операции сложения на множестве натуральных чисел:
- •Умножение натуральных чисел.
- •Свойства операции умножения на множестве натуральных чисел:
- •Упорядоченность полукольца натуральных чисел.
- •Свойства отношения :
- •Понятия наибольшего и наименьшего элементов некоторого множества. Теоремы о существовании наибольшего и наименьшего элементов в подмножестве множества натуральных чисел.
- •Іі и ііі формы метода математической индукции для натуральных чисел.
- •Архимедовская расположенность полукольца натуральных чисел.
- •Лекции 3-4. Построение множества целых чисел.
- •Сложение и умножение целых чисел.
- •Кольцо целых чисел.
- •Вложение полукольца натуральных чисел в кольцо целых.
- •Строение кольца целых чисел.
- •Положительный конус и его свойства.
- •Свойства отношения :
- •Упорядоченность кольца целых чисел.
- •Три формы метода математической индукции для целых чисел.
- •Теоремы о существовании наибольшего и наименьшего элементов в подмножестве множества целых чисел.
- •Абсолютная величина целого числа и его свойства.
- •Свойства модуля:
- •Теорема о делении с остатком.
- •Архимедовская расположенность кольца целых чисел.
- •Лекции 5-6. Построение множества рациональных чисел.
- •Сложение и умножение рациональных чисел.
- •Поле рациональных чисел.
- •Вложение кольца целых чисел в поле рациональных.
- •Упорядоченность поля рациональных чисел.
- •Архимедовская расположенность поля рациональных чисел.
- •Лекция 7. Фундаментальные последовательности рациональных чисел и их свойства
- •Операции над последовательностями рациональных чисел.
- •Нулевые, положительные, отрицательные последовательности рациональных чисел.
- •Эквивалентные последовательности рациональных чисел и их свойства.
- •Лекции 8-9. Построение множества действительных чисел.
- •Поле действительных чисел.
- •Вложение поля рациональных чисел в поле действительных чисел.
- •Упорядоченность поля действительных чисел.
- •Архимедовская расположенность поля действительных чисел.
- •Теорема о сходимости любой фундаментальной последовательности рациональных чисел в поле действительных чисел.
- •Теорема о сходимости любой фундаментальной последовательности действительных чисел в поле действительных чисел.
- •Лекция 10. Поле комплексных чисел.
- •Алгебраическая форма записи комплексного числа.
- •Свойства сопряженных комплексных чисел:
- •Свойства нормы:
- •Геометрическая интерпретация комплексного числа. Тригонометрическая форма записи комплексного числа.
- •Корни - ой степени из единицы
- •Лекция 11. Тело кватернионов.
- •Алгебраическая форма кватернионов.
- •Свойства сопряженных и нормы.
- •Геометрическая интерпретация чисто мнимых кватернионов
- •Лекция 12. Ассоциативные алгебры.
- •Теорема Фробениуса.
- •Дуальные и двойные числа (ассоциативные алгебры над полем действительных чисел размерности 2).
- •Алгебра Кэли (Неассоциативная альтернативная алгебра с делением).
Архимедовская расположенность кольца целых чисел.
Теорема 16.
Кольцо целых чисел является архимедовски
расположенным, т.е. выполняются следующее
условие (аксиома
Архимеда):
![]() ,
где
,
где![]() ,
,![]() такое, чтоa<nb.
такое, чтоa<nb.
Доказательство.
Пусть a
и b-
натуральные числа. Докажем справедливость
утверждения методом математической
индукции по
![]() .
.
База индукции b=1.
![]() .
.
Индуктивное предположение.
Пусть верно для
![]() ,
т.е.
,
т.е.![]() .
.
Проверим для
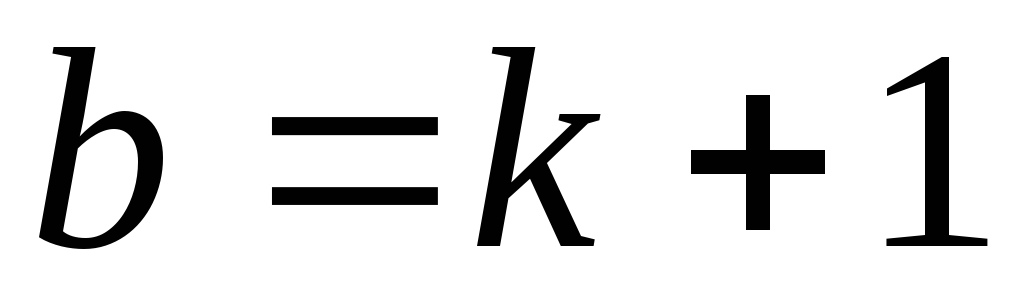 ,
т.е.
,
т.е.
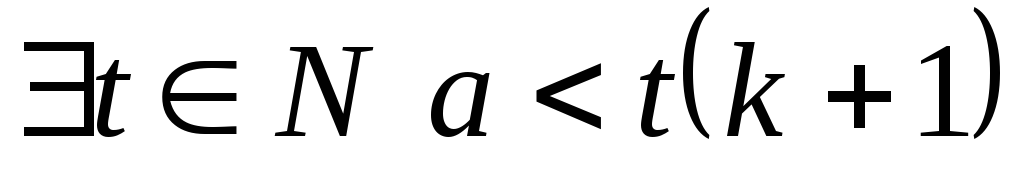 (?)
(?)
Тогда
![]() .
.
Пусть теперь
![]() .Возможны
случаи:
.Возможны
случаи:
![]() ,
,
![]() (доказано выше).
(доказано выше).
что и требовалось доказать.
Теорема 17. Кольцо целых чисел не является всюду плотным.
Доказательство.
Поскольку
![]() ,
а
,
а![]() не является всюду плотным, то и
не является всюду плотным, то и![]() также всюду плотным не будет.
также всюду плотным не будет.
что и требовалось доказать.
Лекции 5-6. Построение множества рациональных чисел.
Рассмотрим множество
![]() ,
на котором введем отношение
,
на котором введем отношение![]() по следующему правилу:
по следующему правилу:
![]()
Теорема 1.
Отношение ≈ на множестве
![]() есть отношение эквивалентности
(рефлексивно, симметрично, транзитивно).
есть отношение эквивалентности
(рефлексивно, симметрично, транзитивно).
Доказательство.
Отношение рефлексивно (?)
![]() .
.
Отношение симметрично (?)
![]() .
.
Отношение транзитивно (?)
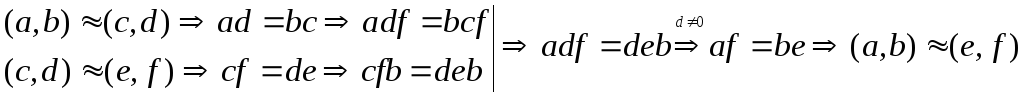 .
.
что и требовалось доказать.
Поскольку ≈ - есть
отношение эквивалентности на множестве
![]() ,
имеют место классы эквивалентности:
,
имеют место классы эквивалентности:
![]() .
.
Определение.
Рациональными числами назовем элементы
фактормножества
![]() .
.
Сложение и умножение рациональных чисел.
Определим на множестве рациональных чисел действия сложения и умножения по следующим правилам:
![]() .
.
Теорема 2.
Действия +
и
![]() являются
бинарными операциями на множестве
являются
бинарными операциями на множестве![]() .
.
Доказательство.
![]() - бинарная операция
(?)
- бинарная операция
(?)
Умножение определено
![]() ,
т.к. определено умножение любых целых
чисел. Покажем однозначность.
,
т.к. определено умножение любых целых
чисел. Покажем однозначность.
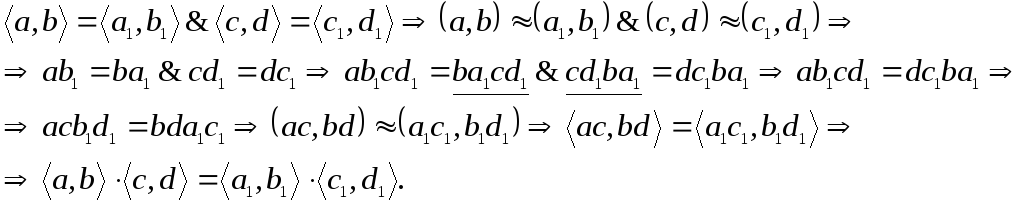
![]() - бинарная операция
(?)
- бинарная операция
(?)
Сложение определено
![]() ,
т.к. определено сложение и умножение
любых целых чисел. Покажем однозначность.
,
т.к. определено сложение и умножение
любых целых чисел. Покажем однозначность.
![]()
Таким образом, для того, чтобы доказать однозначность достаточно проверить равенство:
![]() .
.
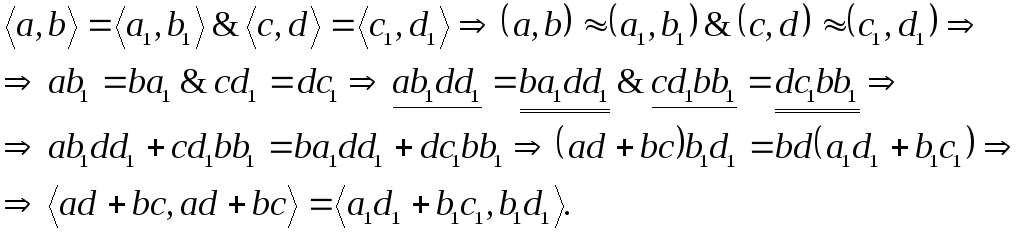
Поскольку
![]() в силу того,
что сумма и произведение целых чисел
также являются целыми числами, множество
в силу того,
что сумма и произведение целых чисел
также являются целыми числами, множество
![]() замкнуто относительно сложения и
умножения.
замкнуто относительно сложения и
умножения.
что и требовалось доказать.
Поле рациональных чисел.
Лемма 1.
![]() .
.
Теорема 3.
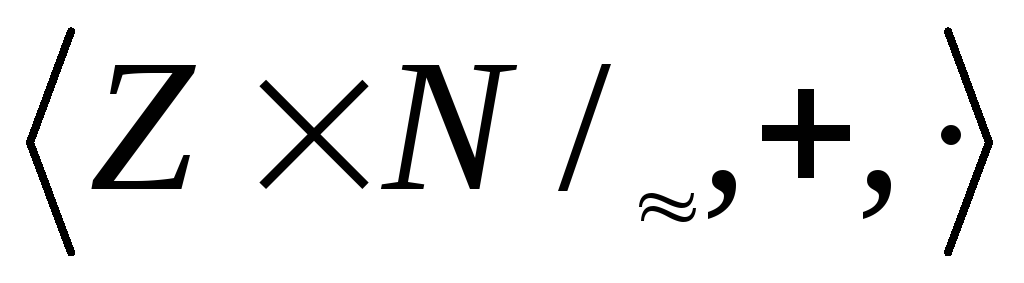 - поле.
- поле.
Доказательство.
Непосредственной проверкой легко устанавливается, что сложение и умножение являются коммутативными и ассоциативными операциями, а также дистрибутивность сложения относительно умножения.
![]() (существование
0) (?)
(существование
0) (?)
Покажем, что класс
![]() ,
,![]() :
:
![]() .
.
![]() (существование
1) (?)
(существование
1) (?)
Покажем, что класс
![]() ,
,![]() :
:
![]() .
.
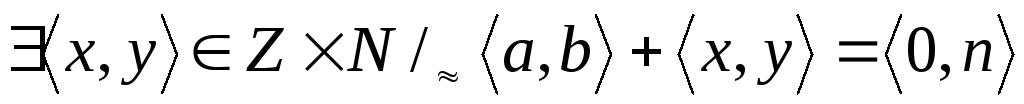
(существование противоположного) (?)
Проверим, что ![]() :
:
![]() .
.
![]()
(существование обратного для каждого ненулевого) (?)
Проверим, что ![]() :
:
![]() - обратный к
- обратный к
![]() .
.
![]() .
.
что и требовалось доказать.
Вложение кольца целых чисел в поле рациональных.
Договоримся
обозначать поле рациональных чисел
через
![]() .
.
Теорема 4.
Кольцо
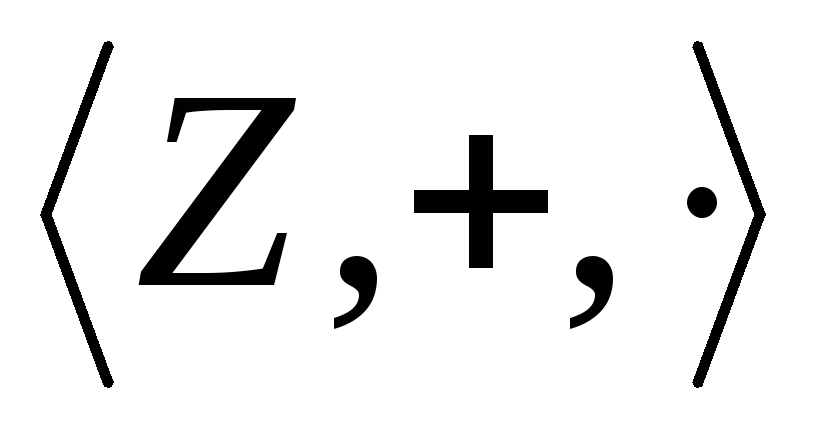 изоморфно вкладывается в поле рациональных
чисел
изоморфно вкладывается в поле рациональных
чисел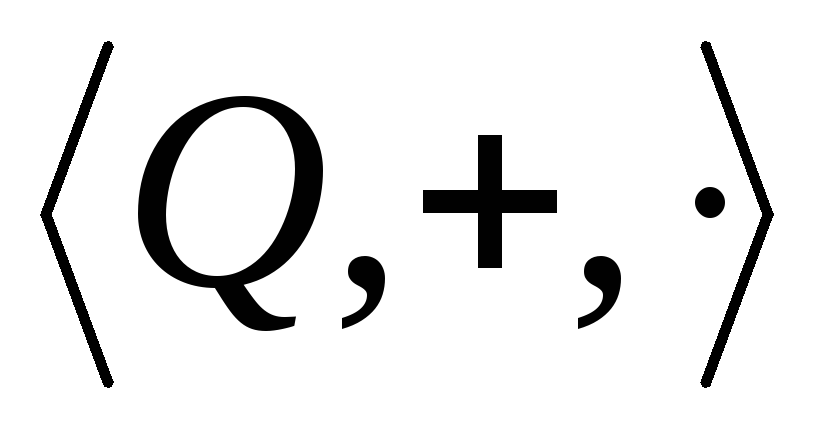 .
.
Доказательство.
Рассмотрим множество
![]() .
Нетрудно устанавливается, что
.
Нетрудно устанавливается, что![]() подполе поля
подполе поля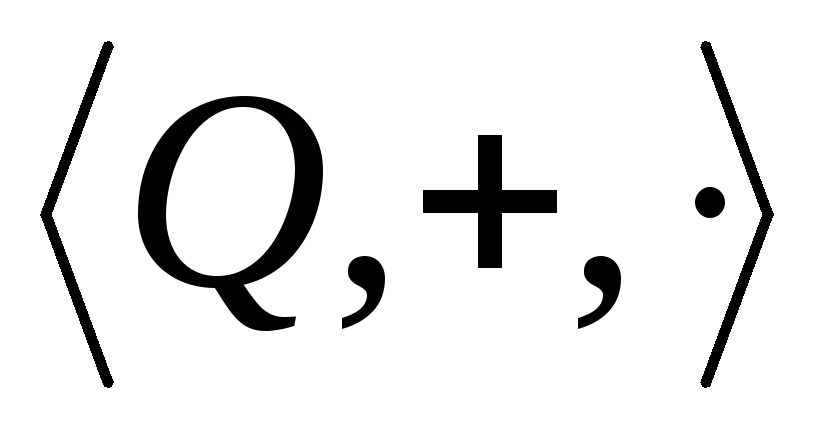 ,
проверим только замкнутость.
,
проверим только замкнутость.
![]() замкнуто
относительно сложения и умножения (?)
замкнуто
относительно сложения и умножения (?)
![]() ;
;
![]() .
.
Рассмотрим
соответствие![]()
![]() заданное по правилу
заданное по правилу![]()
![]() .
.
Докажем, что
![]() - кольцевой изоморфизм.
- кольцевой изоморфизм.
![]() - отображение
(?)
- отображение
(?)
Всюду определенность
очевидна, поскольку для каждого целого
числа
![]() можно построить класс
можно построить класс![]() .
.
Однозначность:![]() (?)
(?)
![]()
![]() - биекция (?)
- биекция (?)
Инъективность:
![]() (?)
(?)
![]() .
.
Сюръективность:
![]()
![]()
![]() (?)
(?)
Возьмем
![]() ,
поскольку
,
поскольку![]() .
В силу произвольности
.
В силу произвольности ![]() сюръективность доказана.
сюръективность доказана.
![]() - гомоморфизм
(?)
- гомоморфизм
(?)
Сохранение
операции сложения:
![]() (?)
(?)
![]() .
.
Сохранение
операции умножения:
![]() (?)
(?)
![]()
Таким образом
доказано, что алгебра
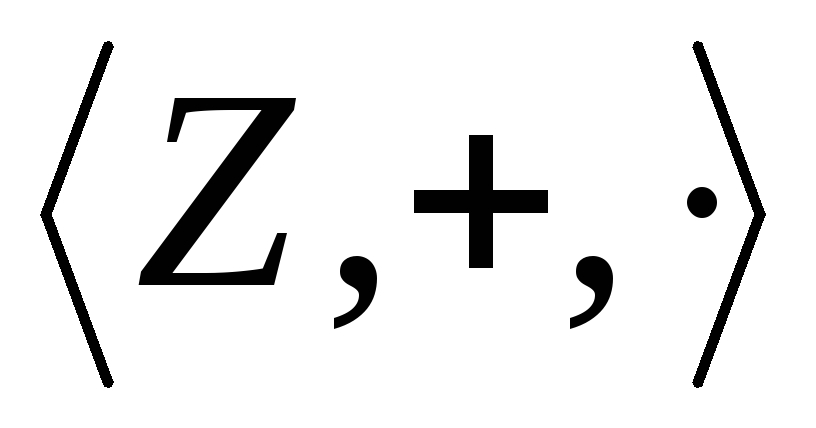 изоморфна подалгебре
изоморфна подалгебре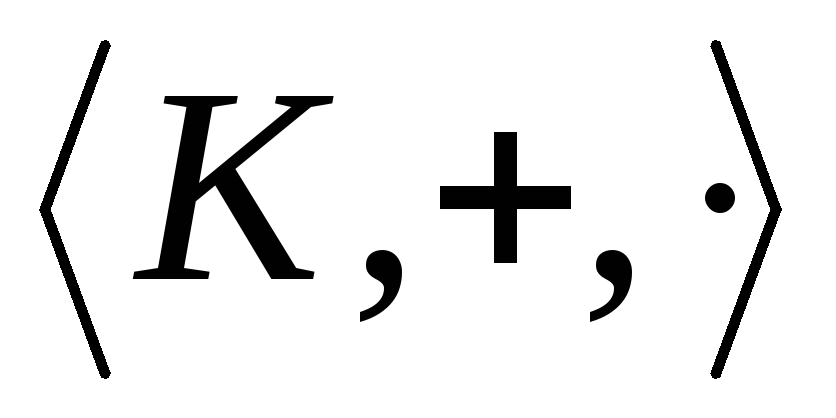 алгебры
алгебры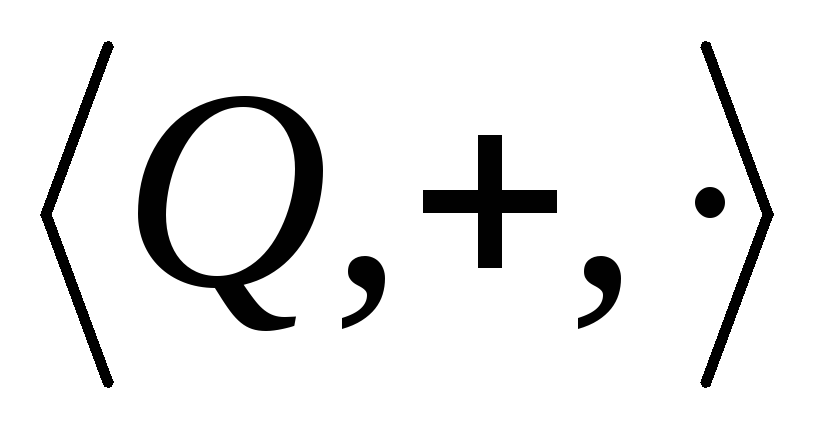 ,
следовательно,
,
следовательно,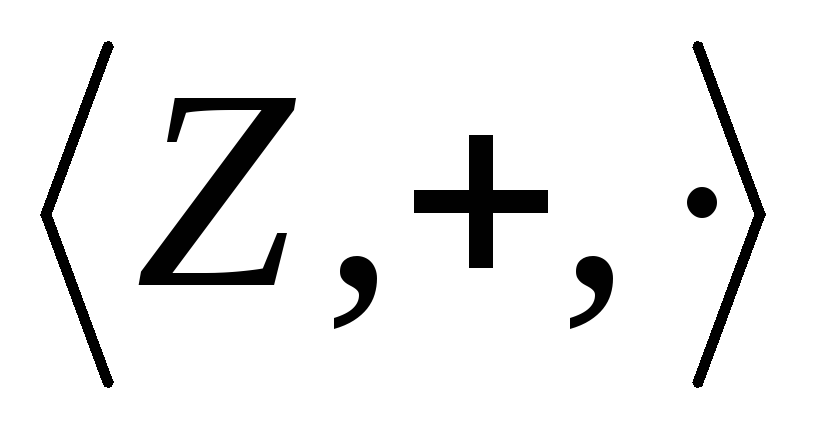 изоморфно вкладывается в
изоморфно вкладывается в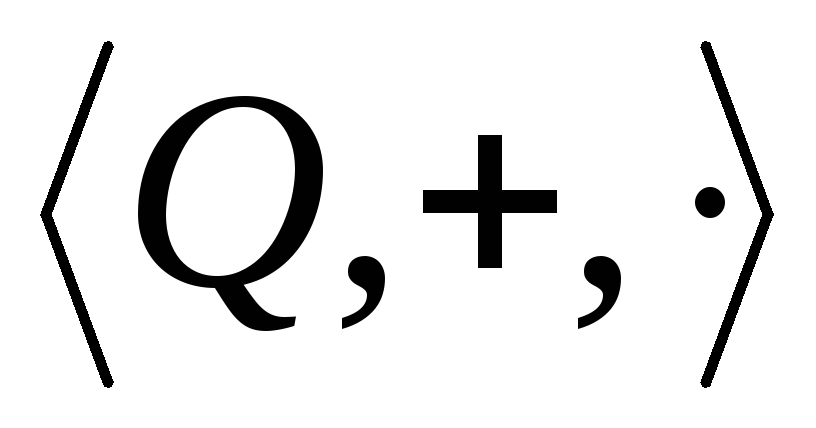 .
.
что и требовалось доказать.
Замечание.
Ввиду
изоморфизма, который отмечен в конце
доказательства, мы проведем отождествление
![]() для каждого целого числа. Ввиду этого
отождествления получим
для каждого целого числа. Ввиду этого
отождествления получим![]() (подмножество, более того, подкольцо).
(подмножество, более того, подкольцо).
