Дуальные и двойные числа (ассоциативные алгебры над полем действительных чисел размерности 2).

Опишем все ассоциативные алгебры над полем размерности 2.

Нетрудно устанавливается, что множества иобразуют ассоциативные алгебры, которые договоримся называть алгебрам двойных чисел и дуальных чисел соответственно.

Теорема. Любая коммутативная ассоциативная алгебра с единицей над полем действительных чисел размерности 2 изоморфна одной из из алгебр,,.

Доказательство

Пусть , где- коммутативная ассоциативная алгебра с единицей. Рассмотрим. Нетрудно устанавливается, чтоизоморфно полю. Тогда, с точностью до изоморфизма, можно утверждать, что(подполе поля А). Последнее означает, что внайдется элементтакой, что системаобразует базис алгебрынад полем.

для некоторых .

. Возможны случаи:

1. . Существует положительное действительное числотакое, что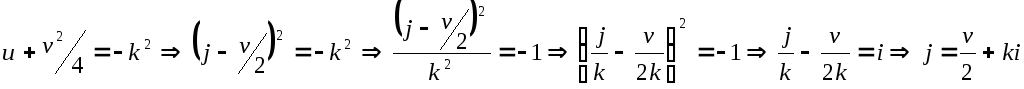

Тогда - система порождающих в. Покажем, что- базис в. Предположим, что. Таким образом.

2. . Аналогично устанавливается, что- базис в. Следовательно,.

3. . Существует положительное действительное числотакое, что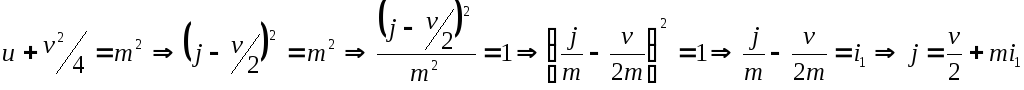

Тогда - система порождающих в. Аналогично устанавливается, что- базис в. Следовательно,.

Замечание. Наличие единицы позволяет включитьв, а ассоциативность и коммутативность позволяют выполнять действия, указанные выше.

что и требовалось доказать.

Теорема. Алгебры ,не являются полями.

Доказательство

Предположим, что элемент обратим. Тогда существует элементтакой, что. Последнее противоречит линейной независимости элементов. Следовательно, предположение об обратимости элементаоказывается ложным, а, значит,не является полем.

Аналогично устанавливается необратимость элемента . Тогдатакже не является полем.

что и требовалось доказать.

Теорема. Алгебры ,существуют.

Доказательство

. Тогда ,. Таким

образом .

. Тогда ,. Таким

образом .

что и требовалось доказать.

Замечание. Алгебры ,иявляются подалгебрами алгебры.

Алгебра Кэли (Неассоциативная альтернативная алгебра с делением).

, где .

На множестве зададим операции по следующим правилам:

для любых и.

Теорема. -восьмимерное линейное пространство над полем , базисом которого является следующая система:.

Замечание. .

Доказательство.

Покажем, что - линейное пространство над полем.

Сложение в коммутативно и ассоциативно в силу коммутативности и ассоциативности сложения в.

Нейтральный элемент по сложению в имеет вид:.

Противоположным к является элемент.

Таким образом - аддитивная Абелева группа, в которой дляиоднозначно определено умножение на скаляр, удовлетворяющее следующим аксиомам:

для любых и.

Согласно определению, - линейное пространство над полем.

По теореме о последовательном расширении полей, имеем

.

что и требовалось доказать.

Определим в умножение по следующему правилу:

, где - кватернионы, сопряженные к,.

Теорема. -восьмерная алгебра с делением над полем .

Доказательство.

Первоначально покажем, что алгебра не является ассоциативной.

. Рассмотрим кватернионы .не является ассоциативной.

Легко самостоятельно проверить, что в алгебре справедливы дистрибутивные законы:и; умножение удовлетворяет следующему условию:для любыхи;- нейтральный элемент по умножению.

Определим в алгебре для элементасопряженный элемент, где- сопряженный кв теле кватернионов. Всправедливы следующие свойства:

для любых .

Нормой элемента договоримся называть. Причем

В справедливы следующие свойства:

1.т.т.т., к.;

2. ;

3. ;

4..

для любых .

Замечание. Из свойств т.т.т., к.иследует, что если, то либо, либо.

Согласно вышеприведенному замечанию, в алгебре отсутствуют делители нуля.

Убедимся, что алгебра с делением. Рассмотрим уравнение , где. Элементявляется решением данного уравнения. Проверим это.

. Аналогично устанавливается, что элемент является решением данного уравнения, где.

что и требовалось доказать.

Определение. Алгебра над полемназывается альтернативной, если выполняется следующие аксиомы:

для любых .

Теорема. Алгебра над полемявляется альтернативной.

Замечание. Алгебра над полемявляется альтернативной, но не ассоциативной. В классе всех альтернативных алгебр лежат и ассоциативные.

61