Федеральное агентство по образованию

Государственное образовательное учреждение

профессионального высшего образования

Волгоградский государственный педагогический университет

Кафедра алгебры, геометрии и информатики

Числовые системы

Курс лекции (24 ч.)

Специальность 050201 «Математика»

с дополнительной специальностью 050202 «Информатика»

4 курс 8 семестр

Волгоград 2009

Лекции 1-2.

Множество натуральных чисел.

Определение. Натуральными числами назовем элементы множества N, в котором выделен элемент и определено отображение(-следующий за, удовлетворяющее следующим аксиомам:

1. (1 не следует ни за каким натуральным числом);

2. (инъективность);

3. .

Аксиомы 1-3 будем называть аксиомами Пеано.

Следствия из аксиом Пеано:

1) (однозначность).

2) .

Доказательство. Предположим, что . Тогда, по аксиоме 2,. Поучили противоречие с условием, следовательно, предположение ложно.

3) .

Доказательство. Пусть ., т.к.. Покажем, что.. Тогда, по 3 аксиоме Пеано,.

4) .

Доказательство. Пусть ., т.к.. Покажем, что.. Тогда, по 3 аксиоме Пеано,.

5) І форма метода математической индукции для множества натуральных чисел: Если утверждение о натуральных числах верно для 1 и из истинности этого утверждения для всякого числаследует истинность его для, тосправедливо для каждого натурального числа.

.

Доказательство. Пусть ., т.к.. Из условия теоремы имеем, что. Тогда, по 3 аксиоме Пеано,.

Независимость аксиом Пеано.

Для доказательства независимости каких-либо двух аксиом от третьей достаточно построить модель теории, в которой указанные две выполняются, а третья – нет.

Доказательство.

Построим модель теории, в которой

1) выполняются аксиомы 2 и 3, а 1-нет.

Очевидно, что 1 аксиома не выполняется, т.к. 1 следует за 1''.

2) выполняются аксиомы 1 и 3, а 2-нет.

Аксиома 2 не выполняется, т.к. .

3) выполняются аксиомы 1 и 2, а 3-нет.

Аксиома 3 не выполняется, т.к.

.

Непротиворечивость системы аксиом Пеано.

Система аксиом Пеано не является противоречивой, поскольку существует модель, на которой выполняются эти аксиомы.

Категоричность теории натуральных чисел.

Для доказательства категоричности достаточно показать, что две произвольные модели множества натуральных чисел изоморфны между собой.

Доказательство.

Рассмотрим две произвольные модели и. Пусть соответствиезадано по следующим правилам:

1. ;

2. .

Покажем, что является биекцией. Тем самым и докажем изоморфизм моделей.

Всюду определенность (?)

. , т.к.. Покажем, что.. Тогда, по 3 аксиоме Пеано,.

Однозначность (?)

Покажем, что . Доказательство проведем методом математической индукции в І форме для натуральных чисел по.

База индукции :

, т.е. (?)

Предположим, что ., последнее противоречит 1 аксиоме Пеано. Таким образом, предположение неверно.

Индуктивное предположение :

.

Покажем справедливость утверждения для :

(?)

Предположим, что .

.

Итак, доказано, что является отображением. Остается проверить сюръективность и инъективность. Для чего рассмотрим следующую систему множеств:,,…,,…, где. Докажем методом математической индукции в І форме для натуральных чисел по, что каждое из этих множеств непустое и одноэлементное, тем самым убедимся в сюръективности и инъективности, соответственно.

База индукции :

(?)

Очевидно, что , т.к.. Предположим, что.

. Последнее противоречит 1 аксиоме Пеано, следовательно, предположение неверно.

Индуктивное предположение :

.

Покажем справедливость утверждения для :

(?)

. Предположим, что . Тогда. Возможны случаи:

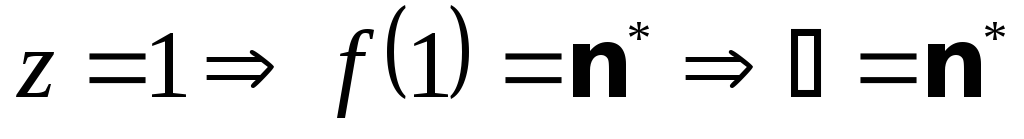• . Последнее противоречит 1 аксиоме Пеано.

• 

, что противоречит условию .

Таким образом, в обоих случаях получено противоречие, следовательно, предположение неверно.

что и требовалось доказать.