
- •Федеральное агентство по образованию
- •Независимость аксиом Пеано.
- •Непротиворечивость системы аксиом Пеано.
- •Категоричность теории натуральных чисел.
- •Сложение натуральных чисел.
- •Свойства операции сложения на множестве натуральных чисел:
- •Умножение натуральных чисел.
- •Свойства операции умножения на множестве натуральных чисел:
- •Упорядоченность полукольца натуральных чисел.
- •Свойства отношения :
- •Понятия наибольшего и наименьшего элементов некоторого множества. Теоремы о существовании наибольшего и наименьшего элементов в подмножестве множества натуральных чисел.
- •Іі и ііі формы метода математической индукции для натуральных чисел.
- •Архимедовская расположенность полукольца натуральных чисел.
- •Лекции 3-4. Построение множества целых чисел.
- •Сложение и умножение целых чисел.
- •Кольцо целых чисел.
- •Вложение полукольца натуральных чисел в кольцо целых.
- •Строение кольца целых чисел.
- •Положительный конус и его свойства.
- •Свойства отношения :
- •Упорядоченность кольца целых чисел.
- •Три формы метода математической индукции для целых чисел.
- •Теоремы о существовании наибольшего и наименьшего элементов в подмножестве множества целых чисел.
- •Абсолютная величина целого числа и его свойства.
- •Свойства модуля:
- •Теорема о делении с остатком.
- •Архимедовская расположенность кольца целых чисел.
- •Лекции 5-6. Построение множества рациональных чисел.
- •Сложение и умножение рациональных чисел.
- •Поле рациональных чисел.
- •Вложение кольца целых чисел в поле рациональных.
- •Упорядоченность поля рациональных чисел.
- •Архимедовская расположенность поля рациональных чисел.
- •Лекция 7. Фундаментальные последовательности рациональных чисел и их свойства
- •Операции над последовательностями рациональных чисел.
- •Нулевые, положительные, отрицательные последовательности рациональных чисел.
- •Эквивалентные последовательности рациональных чисел и их свойства.
- •Лекции 8-9. Построение множества действительных чисел.
- •Поле действительных чисел.
- •Вложение поля рациональных чисел в поле действительных чисел.
- •Упорядоченность поля действительных чисел.
- •Архимедовская расположенность поля действительных чисел.
- •Теорема о сходимости любой фундаментальной последовательности рациональных чисел в поле действительных чисел.
- •Теорема о сходимости любой фундаментальной последовательности действительных чисел в поле действительных чисел.
- •Лекция 10. Поле комплексных чисел.
- •Алгебраическая форма записи комплексного числа.
- •Свойства сопряженных комплексных чисел:
- •Свойства нормы:
- •Геометрическая интерпретация комплексного числа. Тригонометрическая форма записи комплексного числа.
- •Корни - ой степени из единицы
- •Лекция 11. Тело кватернионов.
- •Алгебраическая форма кватернионов.
- •Свойства сопряженных и нормы.
- •Геометрическая интерпретация чисто мнимых кватернионов
- •Лекция 12. Ассоциативные алгебры.
- •Теорема Фробениуса.
- •Дуальные и двойные числа (ассоциативные алгебры над полем действительных чисел размерности 2).
- •Алгебра Кэли (Неассоциативная альтернативная алгебра с делением).
Архимедовская расположенность поля действительных чисел.
Теорема 5.
Поле
действительных чисел архимедовски
расположенное, т.е. выполняется аксиома
Архимеда: ![]() .
.
Доказательство.
Пусть
![]() .
Последнее означает, что
.
Последнее означает, что
![]() - положительная,
следовательно,
- положительная,
следовательно,
![]() .
.
![]() - ф.п.р.ч., следовательно,
- ф.п.р.ч., следовательно,
![]() - ограниченная, тогда следовательно,
- ограниченная, тогда следовательно,![]() .
Поскольку поле рациональных чисел
архимедовски расположенное,
.
Поскольку поле рациональных чисел
архимедовски расположенное,![]() .
.
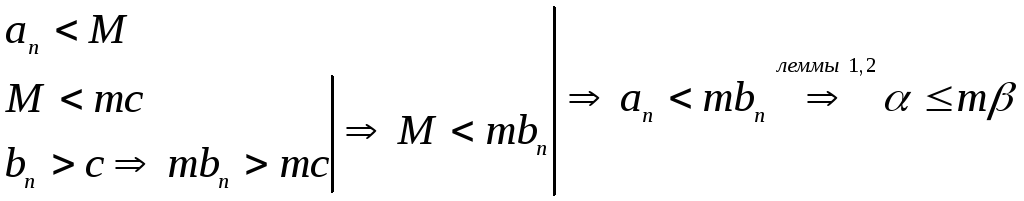 .
.
что и требовалось доказать.
Теорема 6. Поле действительных чисел является всюду плотным.
Доказательство.
Пусть
![]() .
Для определенности положим, что
.
Для определенности положим, что![]() .
Тогда
.
Тогда![]() - положительная, следовательно,
- положительная, следовательно,![]() .
Поскольку
.
Поскольку![]() ,
,![]() - ф.п.р.ч, имеем
- ф.п.р.ч, имеем
![]() .
Возьмем
.
Возьмем
![]() .
Учитывая выше изложенное, получим
.
Учитывая выше изложенное, получим
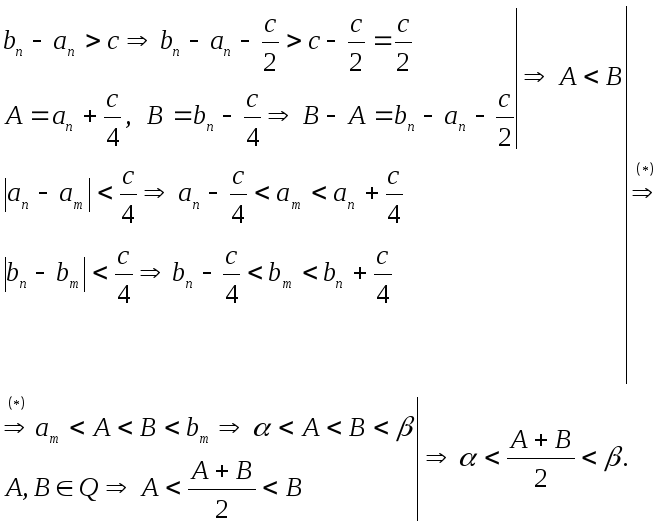
что и требовалось доказать.
Теорема о сходимости любой фундаментальной последовательности рациональных чисел в поле действительных чисел.
Теорема 7.
![]() т.т.т., к.
т.т.т., к.![]() ,
иными словами всякая фундаментальная
последовательность рациональных чисел
сходится в поле действительных чисел.
,
иными словами всякая фундаментальная
последовательность рациональных чисел
сходится в поле действительных чисел.
Доказательство.
Необходимость.
Пусть
![]() .
Возьмем
.
Возьмем![]() такое, что
такое, что![]() ,
где
,
где![]() (в силу фундаментальности последовательности
(в силу фундаментальности последовательности![]() ).
Тогда
).
Тогда![]() .
Согласнолеммам
1, 2, имеем,
что
.
Согласнолеммам
1, 2, имеем,
что
![]() ,
следовательно,
,
следовательно,![]() .
Таким образом,
.
Таким образом,![]() .
.
Достаточность.
Пусть
![]() .
Покажем, что
.
Покажем, что![]() - ф.п.р.ч.
- ф.п.р.ч.
![]() .
Поскольку между действительными числами
.
Поскольку между действительными числами
![]() и
и![]() найдется положительной рациональное
число
найдется положительной рациональное
число![]() .
Тогда
.
Тогда![]() .
Оценим
.
Оценим![]() ,
где
,
где![]() :
:
![]() .
Таким образом, последовательность
рациональных чисел
.
Таким образом, последовательность
рациональных чисел
![]() фундаментальна, а, значит, порождает
некоторый класс эквивалентности
фундаментальна, а, значит, порождает
некоторый класс эквивалентности![]() .
Остается доказать, что
.
Остается доказать, что![]() .
Возможны случаи:
.
Возможны случаи:
1.
![]() .
.
 Последнее
противоречит условию
Последнее
противоречит условию
![]() ,
следовательно, данный случай невозможен.
,
следовательно, данный случай невозможен.
2.
![]() .
.
 Последнее
противоречит условию
Последнее
противоречит условию
![]() ,
следовательно, данный случай невозможен.
,
следовательно, данный случай невозможен.
3.
![]() .
Единственно возможный случай.
.
Единственно возможный случай.
что и требовалось доказать.
Следствие. Для того, чтобы последовательность рациональных чисел имела в поле действительных чисел предел необходимо и достаточно, чтобы она была фундаментальной.
Теорема о сходимости любой фундаментальной последовательности действительных чисел в поле действительных чисел.
Теорема 8. Любая фундаментальная последовательность действительных чисел сходится в поле действительных чисел.
Доказательство.
Пусть
![]() - ф.п.д.ч.,
где
- ф.п.д.ч.,
где
![]() :
:
Рассмотрим
последовательность
![]() .
Покажем, что она фундаментальна.
.
Покажем, что она фундаментальна.
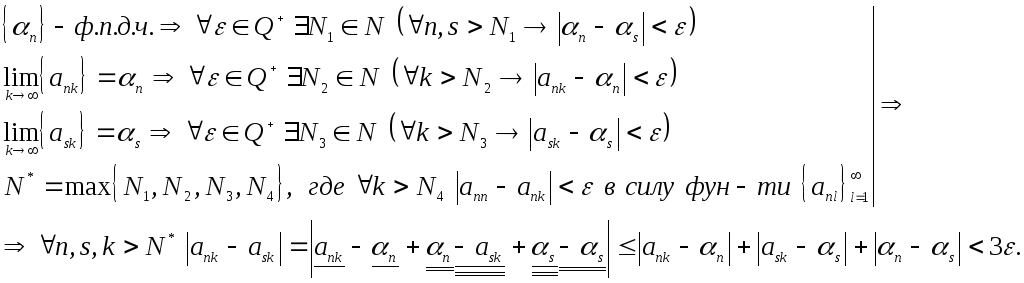 Последнее
неравенство влечет фундаментальность
последовательностей вида
Последнее
неравенство влечет фундаментальность
последовательностей вида
![]() при фиксированном
при фиксированном![]() . Оценим теперь
. Оценим теперь![]() :
:
![]() .
Таким образом, последовательность
.
Таким образом, последовательность
![]() фундаментальна. Докажем, что
фундаментальна. Докажем, что![]() и есть предел последовательности
и есть предел последовательности![]() .
Пусть
.
Пусть![]() .
.
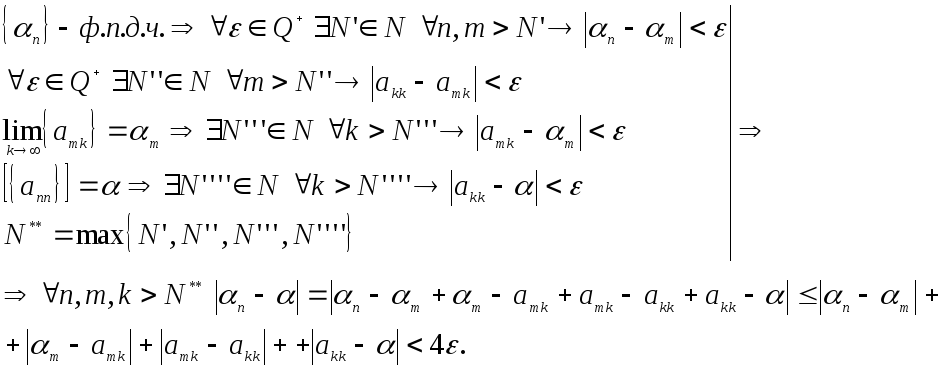
Последнее неравенство
доказывает, что ![]() .
.
что и требовалось доказать.
Лекция 10. Поле комплексных чисел.
Возможны различные подходы к определению поля комплексных чисел.
Один из возможных заключается в следующем:
Определение. Полем комплексных чисел называется алгебраическое расширение поля действительных чисел, иначе, поле комплексных чисел наименьшее из полей, содержащее все алгебраические элементы над полем действительных чисел (т.е. все корни многочленов с действительными коэффициентами).
В этом случае
![]() ,
где
,
где![]() - корень многочлена
- корень многочлена![]() .
.
Другой подход основан на построении поля комплексных чисел как подкольца кольца квадратных матриц второго порядка над полем действительных чисел.
Рассмотрим множество
![]() .
. - кольцо. В этом кольце выбирается
подмножество
- кольцо. В этом кольце выбирается
подмножество![]() .
.
Теорема 1.
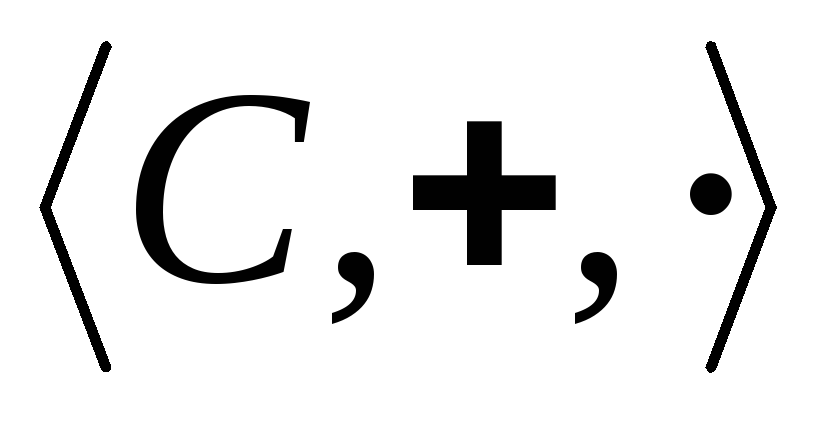 - поле.
- поле.
Доказательство.
Проверим, что
![]() подкольцо кольца
подкольцо кольца![]() ,
а, следовательно, само образует кольцо.
,
а, следовательно, само образует кольцо.
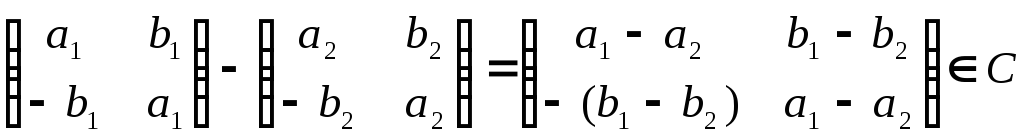
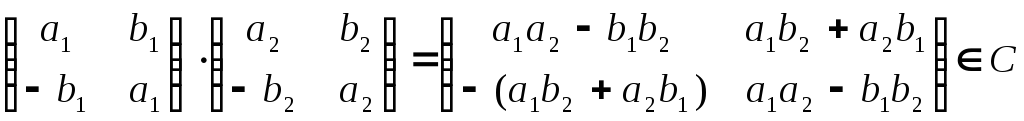 .
.
Нетрудно
устанавливается, что в
![]() умножение коммутативно и ассоциативно.
умножение коммутативно и ассоциативно.
Остается покакать,
что в
![]() каждый ненулевой элемент обратим.
каждый ненулевой элемент обратим.
Пусть
![]() - обратима в
- обратима в![]() .
Тогда
.
Тогда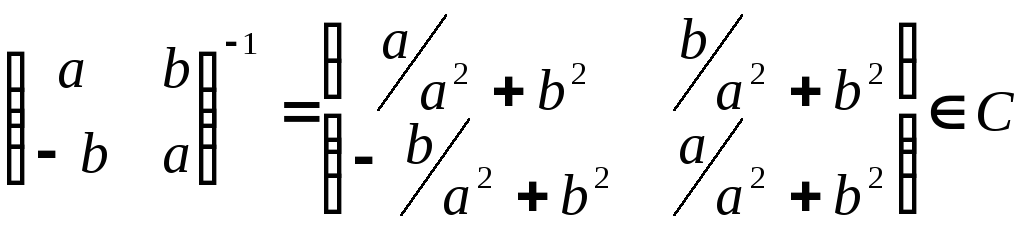 .
.
Таким образом,
 - поле.
- поле.
что и требовалось доказать.
Теорема 2. Поле действительных чисел изоморфно вкладывается в поле комплексных.
Доказательство.
Рассмотрим
соответствие
![]() по правилу
по правилу![]() для всех
для всех![]() .
.
Очевидно, что
![]() - всюдуопределено и однозначно, а,
следовательно,
- всюдуопределено и однозначно, а,
следовательно,![]() - отображение.
- отображение.
![]() - инъективное
отображение.
- инъективное
отображение.
Покажем, что
![]() - гомоморфизм.
- гомоморфизм.
![]()
![]()
Таким образом,
![]() - инъективный гомоморфизм, а, значит,
- инъективный гомоморфизм, а, значит,![]() изоморфно вкладывается в
изоморфно вкладывается в![]() .
.
что и требовалось доказать.
