
- •Федеральное агентство по образованию
- •Независимость аксиом Пеано.
- •Непротиворечивость системы аксиом Пеано.
- •Категоричность теории натуральных чисел.
- •Сложение натуральных чисел.
- •Свойства операции сложения на множестве натуральных чисел:
- •Умножение натуральных чисел.
- •Свойства операции умножения на множестве натуральных чисел:
- •Упорядоченность полукольца натуральных чисел.
- •Свойства отношения :
- •Понятия наибольшего и наименьшего элементов некоторого множества. Теоремы о существовании наибольшего и наименьшего элементов в подмножестве множества натуральных чисел.
- •Іі и ііі формы метода математической индукции для натуральных чисел.
- •Архимедовская расположенность полукольца натуральных чисел.
- •Лекции 3-4. Построение множества целых чисел.
- •Сложение и умножение целых чисел.
- •Кольцо целых чисел.
- •Вложение полукольца натуральных чисел в кольцо целых.
- •Строение кольца целых чисел.
- •Положительный конус и его свойства.
- •Свойства отношения :
- •Упорядоченность кольца целых чисел.
- •Три формы метода математической индукции для целых чисел.
- •Теоремы о существовании наибольшего и наименьшего элементов в подмножестве множества целых чисел.
- •Абсолютная величина целого числа и его свойства.
- •Свойства модуля:
- •Теорема о делении с остатком.
- •Архимедовская расположенность кольца целых чисел.
- •Лекции 5-6. Построение множества рациональных чисел.
- •Сложение и умножение рациональных чисел.
- •Поле рациональных чисел.
- •Вложение кольца целых чисел в поле рациональных.
- •Упорядоченность поля рациональных чисел.
- •Архимедовская расположенность поля рациональных чисел.
- •Лекция 7. Фундаментальные последовательности рациональных чисел и их свойства
- •Операции над последовательностями рациональных чисел.
- •Нулевые, положительные, отрицательные последовательности рациональных чисел.
- •Эквивалентные последовательности рациональных чисел и их свойства.
- •Лекции 8-9. Построение множества действительных чисел.
- •Поле действительных чисел.
- •Вложение поля рациональных чисел в поле действительных чисел.
- •Упорядоченность поля действительных чисел.
- •Архимедовская расположенность поля действительных чисел.
- •Теорема о сходимости любой фундаментальной последовательности рациональных чисел в поле действительных чисел.
- •Теорема о сходимости любой фундаментальной последовательности действительных чисел в поле действительных чисел.
- •Лекция 10. Поле комплексных чисел.
- •Алгебраическая форма записи комплексного числа.
- •Свойства сопряженных комплексных чисел:
- •Свойства нормы:
- •Геометрическая интерпретация комплексного числа. Тригонометрическая форма записи комплексного числа.
- •Корни - ой степени из единицы
- •Лекция 11. Тело кватернионов.
- •Алгебраическая форма кватернионов.
- •Свойства сопряженных и нормы.
- •Геометрическая интерпретация чисто мнимых кватернионов
- •Лекция 12. Ассоциативные алгебры.
- •Теорема Фробениуса.
- •Дуальные и двойные числа (ассоциативные алгебры над полем действительных чисел размерности 2).
- •Алгебра Кэли (Неассоциативная альтернативная алгебра с делением).
Лекция 11. Тело кватернионов.
Открыл Уильям Роуан Гамильтон (ирландец) 1805-1865.
Определение. Ненулевое кольцо с единицей, в котором каждый элемент, отличный от нуля, обратим, называется телом.
Рассмотрим множество матриц:
![]() ,
,
где
![]() - множество квадратных матриц с
коэффициентами из поля комплексных
чисел.
- множество квадратных матриц с
коэффициентами из поля комплексных
чисел.
Теорема 1.
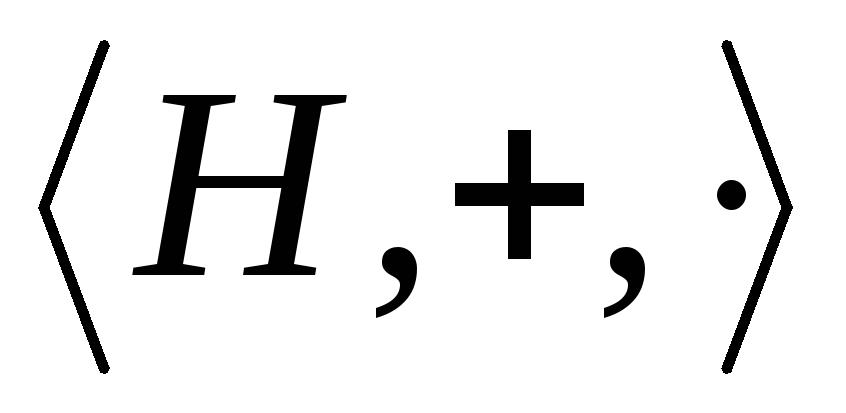 тело.
тело.
Доказательство.
Покажем, что
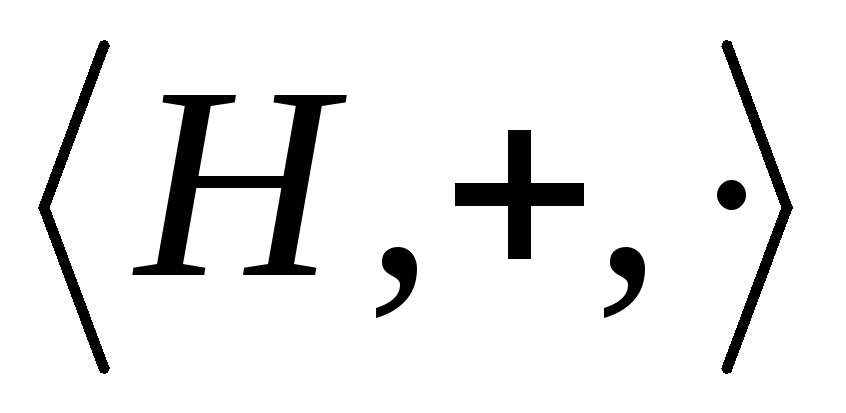 -
подкольцо кольца
-
подкольцо кольца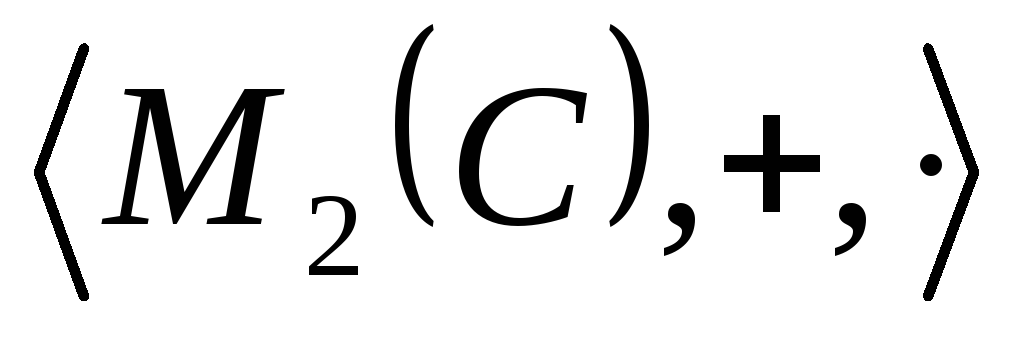 ,
используя признак подкольца:
,
используя признак подкольца:
![]()
![]() .
.
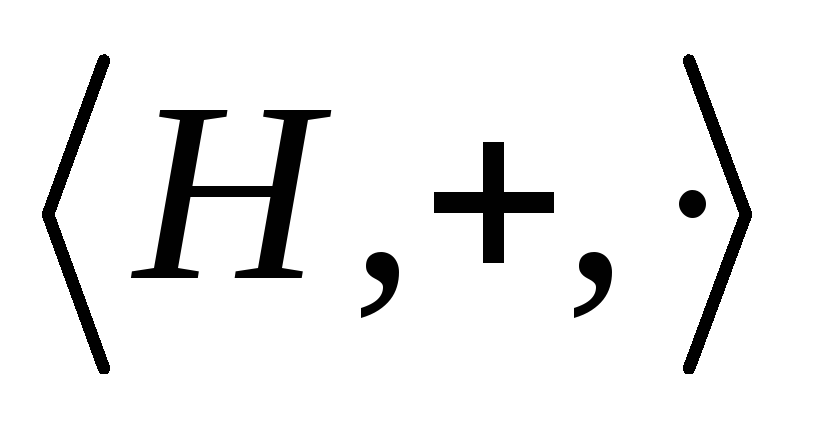 - кольцо с единицей
(?)
- кольцо с единицей
(?)
Элемент
![]() является нейтральным элементом по
сложению, поскольку
является нейтральным элементом по
сложению, поскольку![]() .
.
Проверим, что
любой ненулевой элемент кольца
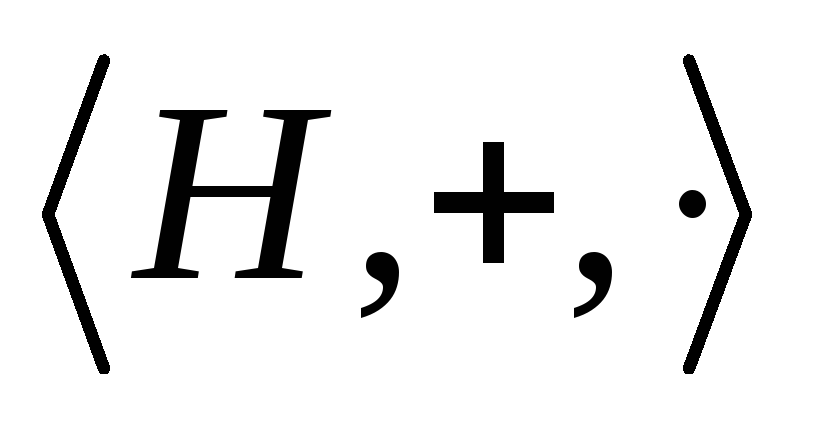 обратим:
обратим:
![]()
![]() или
или
![]() .
.![]() .
Из последнего следует, что любая ненулевая
матрица
.
Из последнего следует, что любая ненулевая
матрица![]() невырожденная, следовательно, она
обратима в кольце
невырожденная, следовательно, она
обратима в кольце
![]() .
Найдем обратную:
.
Найдем обратную:
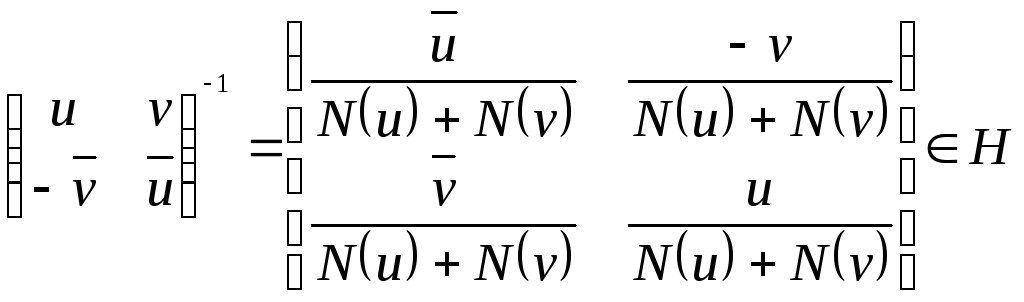 .
.
что и требовалось доказать.
Определение.
Тело
![]() назовем
телом кватернионов, а его элементы
кватернионами.
назовем
телом кватернионов, а его элементы
кватернионами.
Теорема 2. Поле комплексных чисел изоморфно вкладывается в тело кватернионов.
Доказательство.
Рассмотрим
соответствие
![]() ,
заданное по правилу
,
заданное по правилу![]() .
.
Докажем, что
![]() - изоморфизм.
- изоморфизм.
![]() - отображение
(?)
- отображение
(?)
Всюду определенность
очевидна, поскольку для каждого
комплексного числа
![]() можно построить матрицу
можно построить матрицу![]() .
.
Однозначность:![]() (?)
(?)
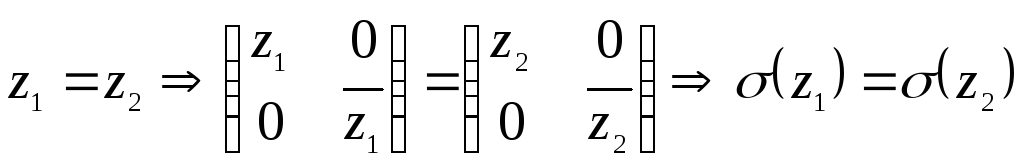 .
.
![]() - биекция (?)
- биекция (?)
Инъективность:
![]() (?)
(?)
 .
.
Сюръективность:
![]()
![]() (?)
(?)
Возьмем
![]() ,
поскольку
,
поскольку![]() .
В силу произвольности
.
В силу произвольности![]() сюръективность доказана.
сюръективность доказана.
![]() - гомоморфизм
(?)
- гомоморфизм
(?)
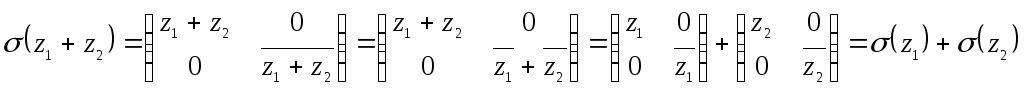
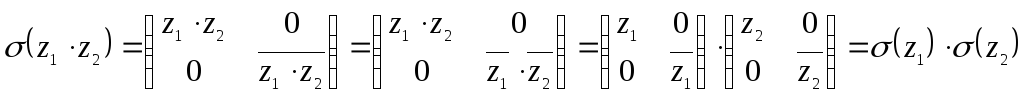 .
.
что и требовалось доказать.
Замечание.
Ввиду
изоморфизма, который отмечен в конце
доказательства, мы проведем отождествление
кватерниона ![]() с комплексным числом
с комплексным числом ![]() .Ввиду этого
отождествления получим
.Ввиду этого
отождествления получим
![]() (подмножество, более того, подтело).
(подмножество, более того, подтело).
Алгебраическая форма кватернионов.
Определение.
Пусть
![]() ,
где
,
где![]() ,
,![]() .
Тогда
.
Тогда![]()
![]() - алгебраическая
форма кватерниона,
где
- алгебраическая
форма кватерниона,
где
![]() и
и
![]() ,
,![]() ,
,
![]() .
Таким образом, каждому кватерниону
можно поставить в соответствие
упорядоченный набор их 4-х элементов:
.
Таким образом, каждому кватерниону
можно поставить в соответствие
упорядоченный набор их 4-х элементов:
Нетрудно заметить следующее:
![]() .
.
Более того, если
рассматривать тело
![]() как векторное пространство над полем
как векторное пространство над полем![]() ,
то каждый кватернион
,
то каждый кватернион![]() есть вектор с координатами
есть вектор с координатами
![]() .
Тогда следующие кватернионы образуют
базис:
.
Тогда следующие кватернионы образуют
базис:
1=(1,0,0,0) - действительная единица
i=(0,1,0,0)
j=(0,0,1,0)
k=(0,0,1,0).
Определение. Кватернионы i, j, k называются мнимыми кватернионами тела кватернионов.
Замечание. Тело кватернионов не является полем, поскольку не коммутативно, что и подтверждает следующая таблица умножения базисных кватернионов:
|
1\2 |
1 |
i |
j |
k |
|
1 |
1 |
i |
j |
k |
|
i |
i |
-1 |
k |
-j |
|
j |
j |
-k |
-1 |
i |
|
k |
k |
j |
-i |
-1 |
Для того, чтобы
перемножить два кватерниона в
алгебраической форме, необходимо
воспользоваться правилом умножения
сумм, учитывая некоммутативность
![]() ,
используя таблицу умножения базисных
кватернионов, а затем привести подобные.
,
используя таблицу умножения базисных
кватернионов, а затем привести подобные.
Определение.
Сопряженным
к кватерниону
![]() называется кватернион
называется кватернион![]() .
.
Следствие.
![]() .
.
Определение.
Нормой
кватерниона
![]() называется
называется![]() .
.
Следствие 1.
![]() ,
где
,
где![]() ,
,![]() .
.
Следствие 2.
Если
![]() ,
то
,
то![]() .
.
Свойства сопряженных и нормы.
Теорема 3.
Для любых
кватернионов
![]() и
и![]() справедливы следующие свойства:
справедливы следующие свойства:
 ;
;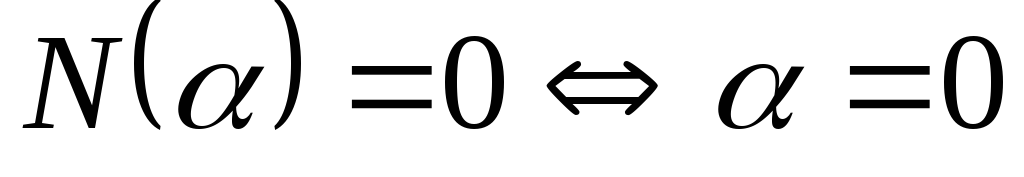 ;
;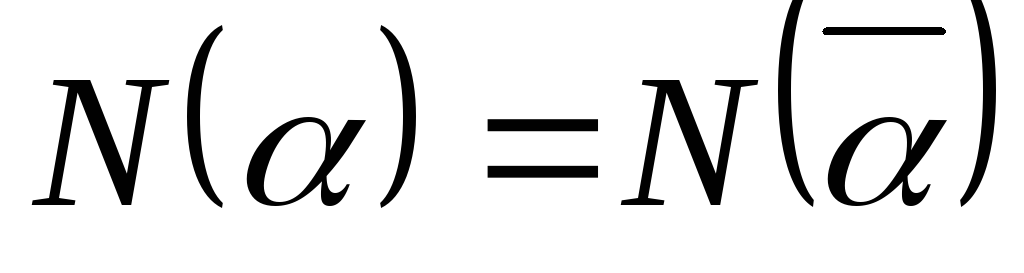 ;
;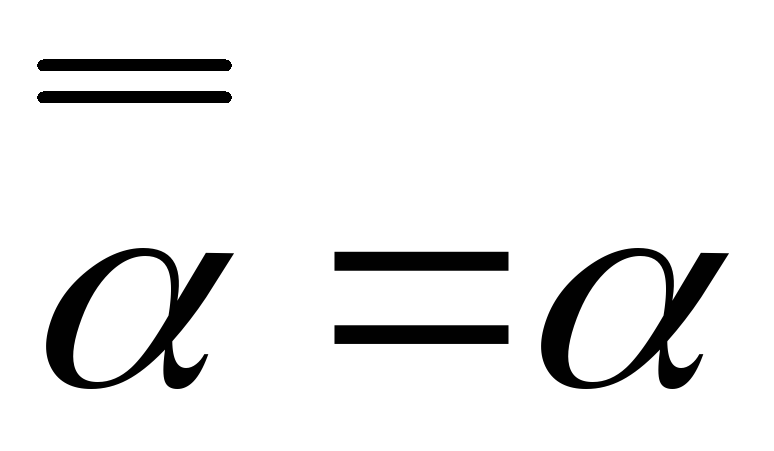 ;
; ;
;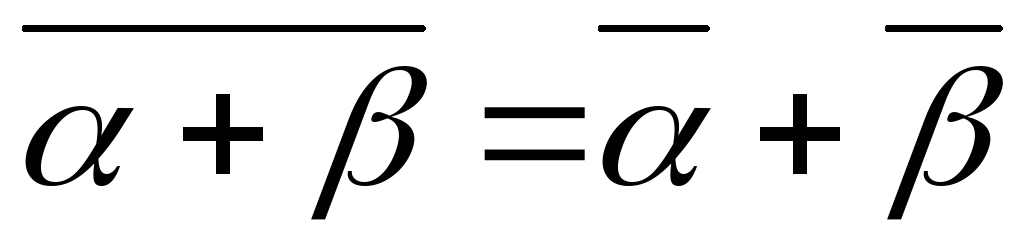 ;
;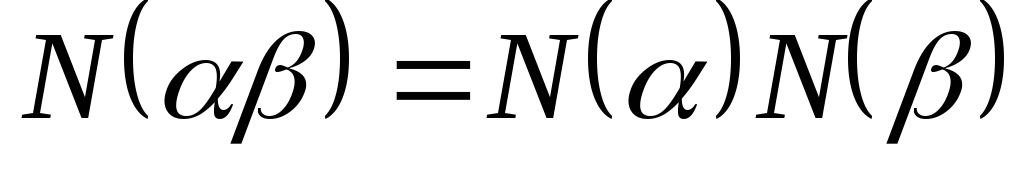 ;
;Если
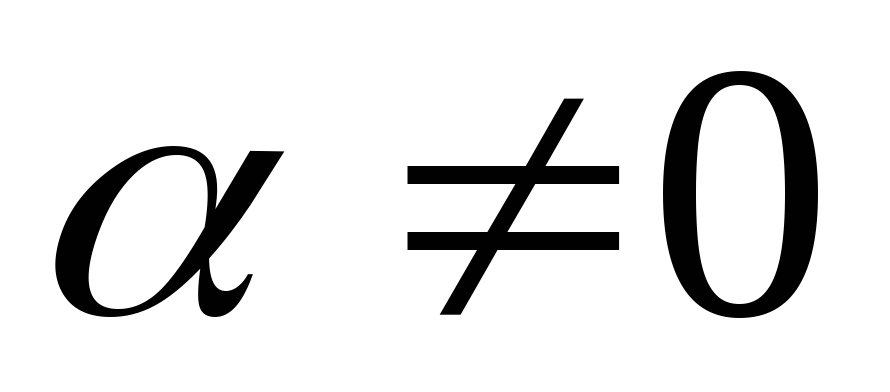 ,
то
,
то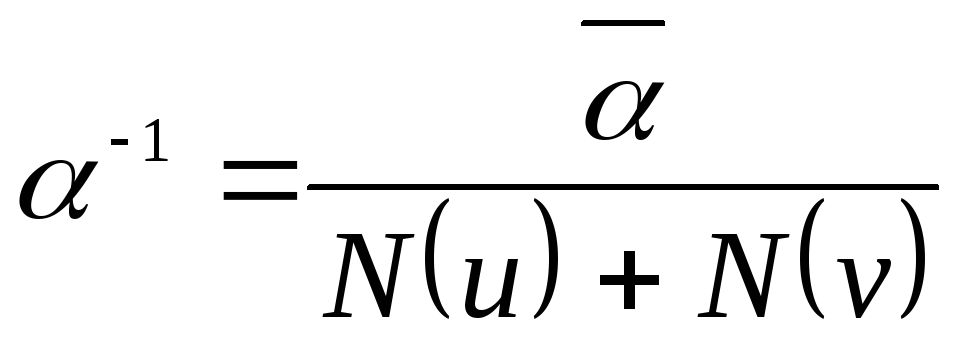 .
.
Доказательство.
Пусть
![]() и
и![]() .
.
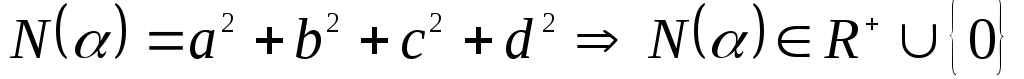 .
.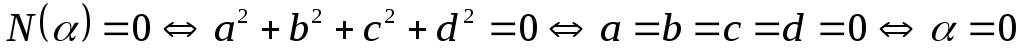 .
.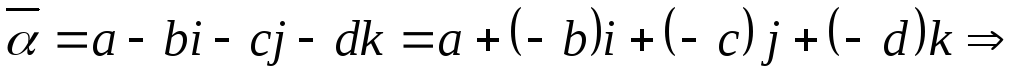
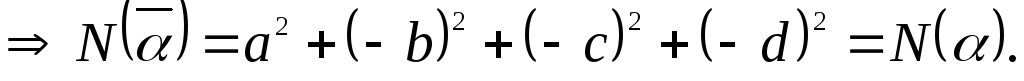
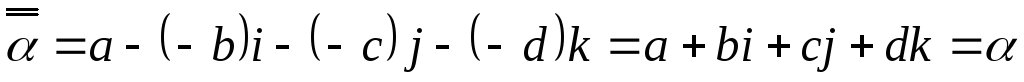 .
.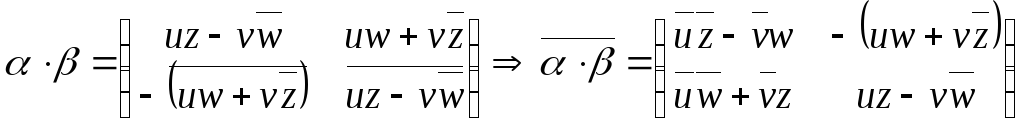 ,
,
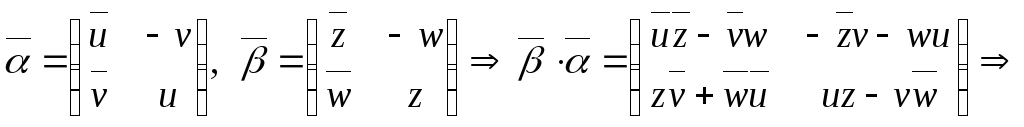
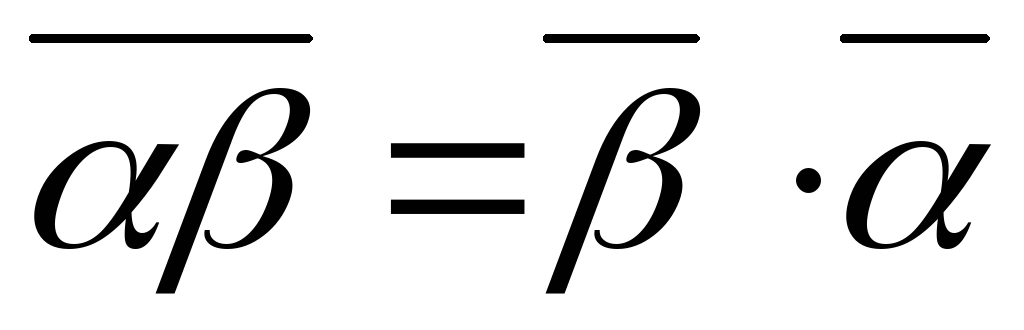 .
.Аналогично 5.
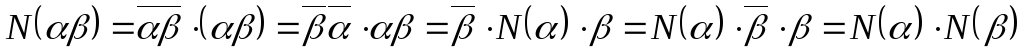 .
.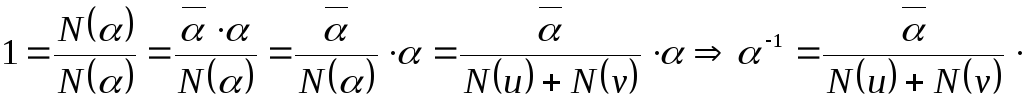
что и требовалось доказать.
