
- •Федеральное агентство по образованию
- •Независимость аксиом Пеано.
- •Непротиворечивость системы аксиом Пеано.
- •Категоричность теории натуральных чисел.
- •Сложение натуральных чисел.
- •Свойства операции сложения на множестве натуральных чисел:
- •Умножение натуральных чисел.
- •Свойства операции умножения на множестве натуральных чисел:
- •Упорядоченность полукольца натуральных чисел.
- •Свойства отношения :
- •Понятия наибольшего и наименьшего элементов некоторого множества. Теоремы о существовании наибольшего и наименьшего элементов в подмножестве множества натуральных чисел.
- •Іі и ііі формы метода математической индукции для натуральных чисел.
- •Архимедовская расположенность полукольца натуральных чисел.
- •Лекции 3-4. Построение множества целых чисел.
- •Сложение и умножение целых чисел.
- •Кольцо целых чисел.
- •Вложение полукольца натуральных чисел в кольцо целых.
- •Строение кольца целых чисел.
- •Положительный конус и его свойства.
- •Свойства отношения :
- •Упорядоченность кольца целых чисел.
- •Три формы метода математической индукции для целых чисел.
- •Теоремы о существовании наибольшего и наименьшего элементов в подмножестве множества целых чисел.
- •Абсолютная величина целого числа и его свойства.
- •Свойства модуля:
- •Теорема о делении с остатком.
- •Архимедовская расположенность кольца целых чисел.
- •Лекции 5-6. Построение множества рациональных чисел.
- •Сложение и умножение рациональных чисел.
- •Поле рациональных чисел.
- •Вложение кольца целых чисел в поле рациональных.
- •Упорядоченность поля рациональных чисел.
- •Архимедовская расположенность поля рациональных чисел.
- •Лекция 7. Фундаментальные последовательности рациональных чисел и их свойства
- •Операции над последовательностями рациональных чисел.
- •Нулевые, положительные, отрицательные последовательности рациональных чисел.
- •Эквивалентные последовательности рациональных чисел и их свойства.
- •Лекции 8-9. Построение множества действительных чисел.
- •Поле действительных чисел.
- •Вложение поля рациональных чисел в поле действительных чисел.
- •Упорядоченность поля действительных чисел.
- •Архимедовская расположенность поля действительных чисел.
- •Теорема о сходимости любой фундаментальной последовательности рациональных чисел в поле действительных чисел.
- •Теорема о сходимости любой фундаментальной последовательности действительных чисел в поле действительных чисел.
- •Лекция 10. Поле комплексных чисел.
- •Алгебраическая форма записи комплексного числа.
- •Свойства сопряженных комплексных чисел:
- •Свойства нормы:
- •Геометрическая интерпретация комплексного числа. Тригонометрическая форма записи комплексного числа.
- •Корни - ой степени из единицы
- •Лекция 11. Тело кватернионов.
- •Алгебраическая форма кватернионов.
- •Свойства сопряженных и нормы.
- •Геометрическая интерпретация чисто мнимых кватернионов
- •Лекция 12. Ассоциативные алгебры.
- •Теорема Фробениуса.
- •Дуальные и двойные числа (ассоциативные алгебры над полем действительных чисел размерности 2).
- •Алгебра Кэли (Неассоциативная альтернативная алгебра с делением).
Свойства операции умножения на множестве натуральных чисел:
1)
![]() .
.
Доказательство.
![]() .
.
2)
![]() .
.
Доказательство.
![]() .
.
3)
![]() (дистрибутивность).
(дистрибутивность).
Доказательство.
Проведем методом
математической индукции в І форме для
натуральных чисел по
![]() .
.
База индукции
![]() :
:
![]() .
.
Индуктивное
предположение
![]() :
:
![]()
Покажем
справедливость утверждения для
![]() :
:
![]() (?)
(?)
![]() .
.
4)
![]() (ассоциативность).
(ассоциативность).
Доказательство.
Проведем методом
математической индукции в І форме для
натуральных чисел по
![]() .
.
База индукции
![]() :
:
![]() .
.
Индуктивное
предположение
![]() :
:
![]()
Покажем
справедливость утверждения для
![]() :
:
![]() (?)
(?)
![]() .
.
5)
![]() (коммутативность).
(коммутативность).
Доказательство.
Проведем методом
математической индукции в І форме для
натуральных чисел по
![]() .
.
База индукции
![]() :
:
![]() .
.
Индуктивное
предположение
![]() :
:
![]()
Покажем
справедливость утверждения для
![]() :
:
![]() (?)
(?)
![]() .
.
6)
![]() (закон
сокращения).
(закон
сокращения).
Доказательство.
см 8) свойство отношения
![]() на
на![]() .
.
Упорядоченность полукольца натуральных чисел.
На множестве
натуральных чисел определим бинарное
отношение
![]() по следующему правилу:
по следующему правилу:
![]()
Теорема 3.
Отношение
![]() на множестве натуральных чисел является
строгим линейным порядком.
на множестве натуральных чисел является
строгим линейным порядком.
Доказательство.
Отношение![]() - порядок на
- порядок на![]() (?)
(?)
![]() (антисимметричность)
(?)
(антисимметричность)
(?)
![]() .
Возможны случаи:
.
Возможны случаи:
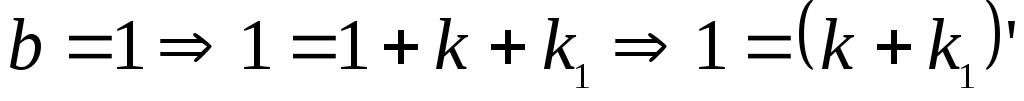 ;
;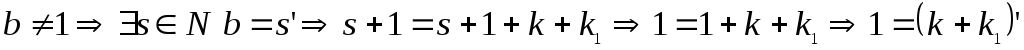 .
.
В обоих случаях получили противоречие с 1 аксиомой Пеано, следовательно, посылка импликации ложна, а, значит, сама импликация истинна.
![]() (транзитивность)
(?)
(транзитивность)
(?)
![]() .
.
Порядок![]() - строгий (?)
- строгий (?)
![]() (антирефлексивность)
(?)
(антирефлексивность)
(?)
Предположим, что
![]() .
Возможны случаи:
.
Возможны случаи:
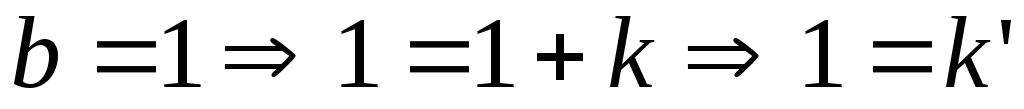 ;
;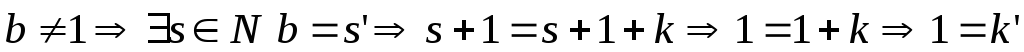 .
.
В обоих случаях получили противоречие с 1 аксиомой Пеано, следовательно, предположение неверно.
Порядок![]() - линейный (?)
- линейный (?)
![]() (линейность)
(?)
(линейность)
(?)
Доказательство
проведем методом математической индукции
в І форме для натуральных чисел по
![]() .
.
База индукции
![]() :
:
Возможны случаи:
 ;
;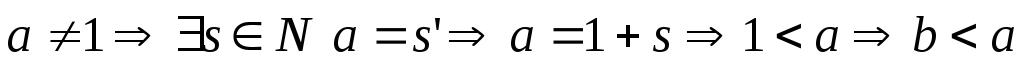 .
.
В обоих случаях дизъюнкция оказалась истинной.
Индуктивное
предположение
![]() :
:
![]()
Покажем
справедливость утверждения для
![]() :
:
![]() (?)
(?)
Возможны случаи:
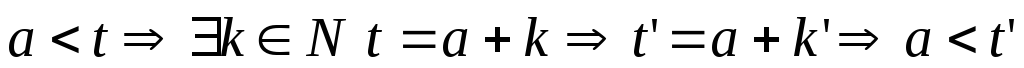 ;
;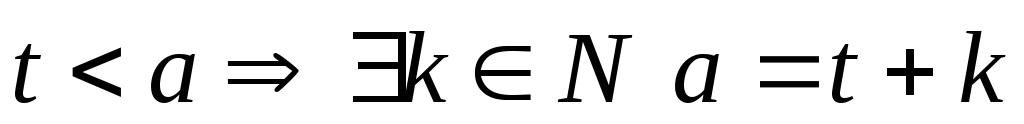 .
Возможны случаи:
.
Возможны случаи:
 ,
,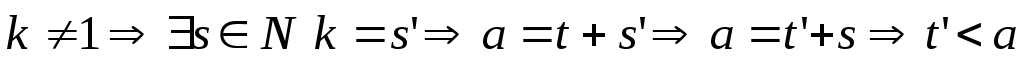 ;
;
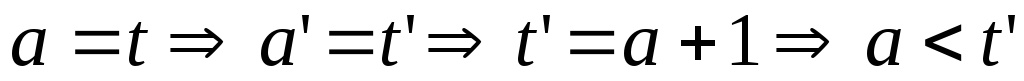 .
.
что и требовалось доказать.
Свойства отношения :
1)
![]() .
.
Доказательство.
![]() .
.
2)
![]() .
.
Доказательство.
![]() .
.
3)
![]() .
.
Доказательство.
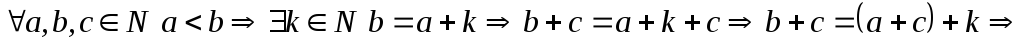
![]() .
.
4)
![]() .
.
Доказательство.
![]() .
.
5)
![]() .
.
Доказательство.
![]()
![]() .
.
6)
![]() .
.
Доказательство.
![]()
![]() .
.
7)
![]() .
.
Доказательство.
![]() возможны случаи:
возможны случаи:
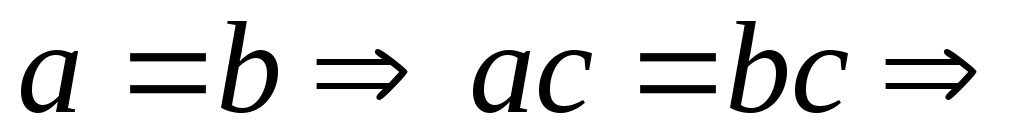 противоречие
с условием
противоречие
с условием
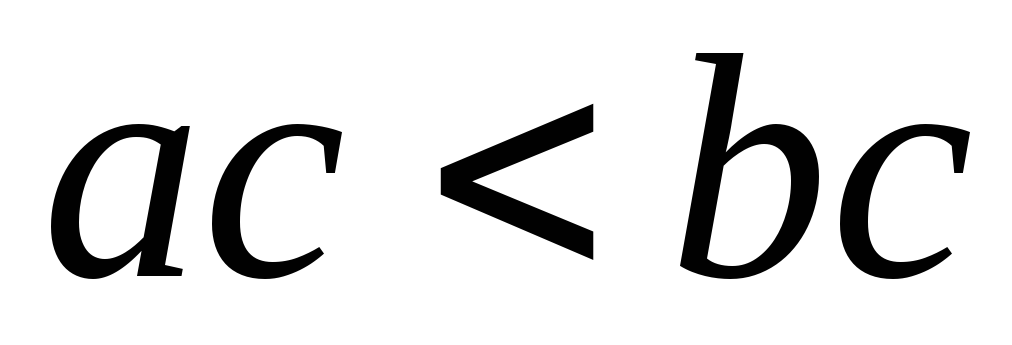 ;
;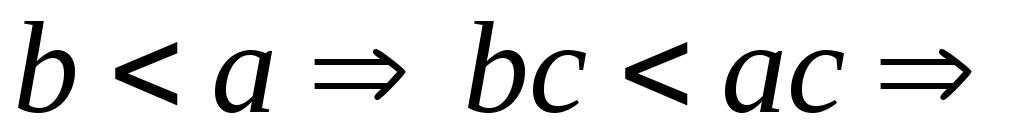 противоречие
с условием
противоречие
с условием
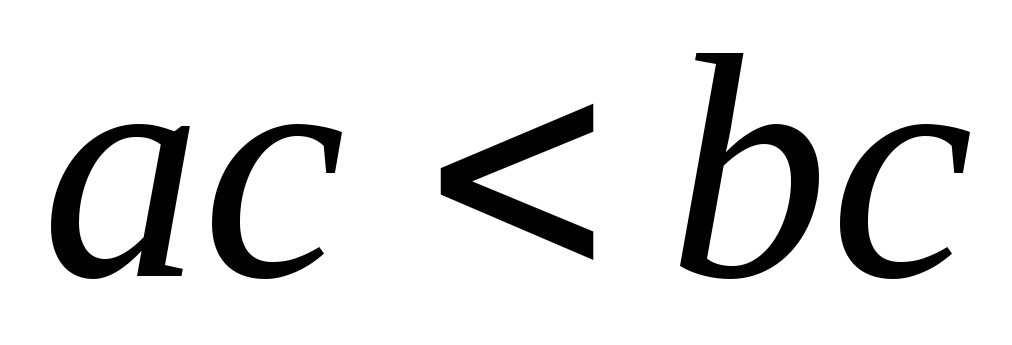 ;
;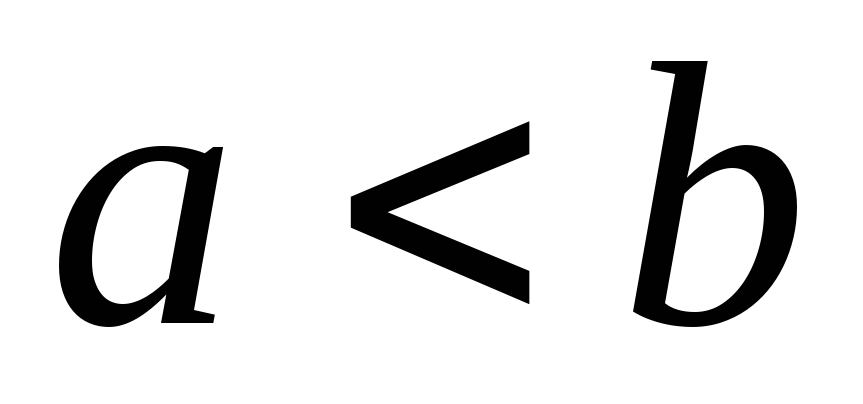 .
.
Методом исключения
получаем, что
![]() .
.
8)
![]() .
.
Доказательство.
Предположим, что
![]() .
Тогда возможны случаи:
.
Тогда возможны случаи:
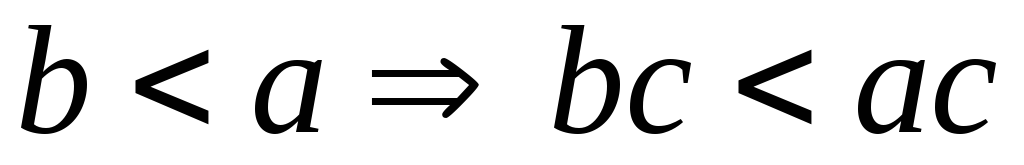 ;
; .
.
В обоих случаях
получено противоречие с условием
![]() ,
следовательно, предположение неверно.
,
следовательно, предположение неверно.
Определение.
Универсальная алгебра
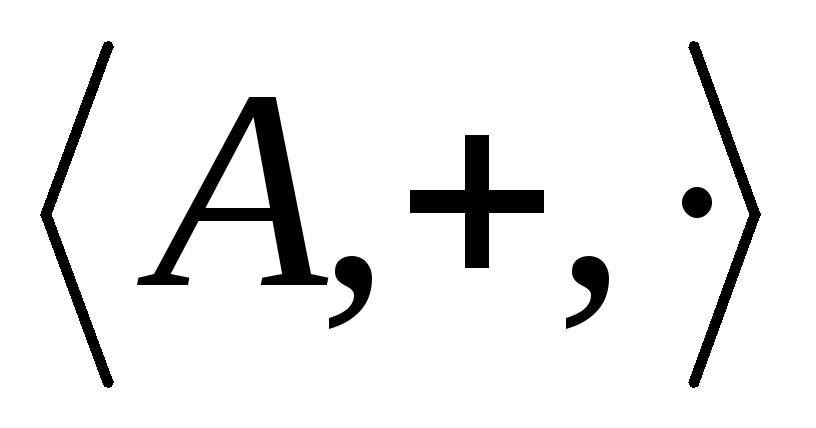 называется полукольцом, если бинарные
операции + и
называется полукольцом, если бинарные
операции + и![]() удовлетворяет следующим условиям:
удовлетворяет следующим условиям:![]()
1.![]() ;
;
2.
![]() ;;
;;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() ;
;
6.
![]() .
.
Теорема 4.
![]() -полукольцо.
-полукольцо.
Доказательство.
Сложение и умножение - операции на множестве натуральных чисел (теоремы 1,2). Доказательство аксиом полукольца смотри свойства указанных опреаций.
что и требовалось доказать.
Определим на
множестве натуральных чисел бинарное
отношение
![]() по следующему правилу:
по следующему правилу:
![]() .
.
Теорема 5.
Отношение
![]() на множестве натуральных чисел является
линейным порядком(рефлексивно,
антисимметрично, транзитивно, линейно).
на множестве натуральных чисел является
линейным порядком(рефлексивно,
антисимметрично, транзитивно, линейно).
(доказательство самостоятельно).
Определение.
Множество
![]() называется линейно упорядоченным, если
на нем задано бинарное отношение
линейного порядка.
называется линейно упорядоченным, если
на нем задано бинарное отношение
линейного порядка.
Определение.
Полукольцо
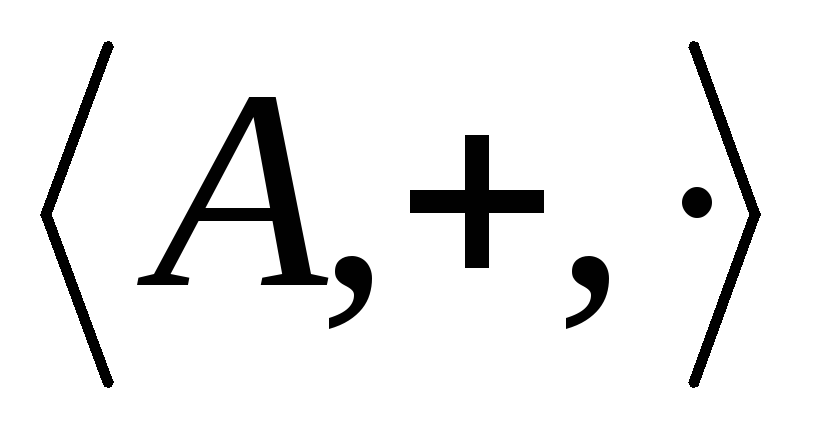 называется линейно упорядоченным, если
множество
называется линейно упорядоченным, если
множество![]() линейно упорядочено.
линейно упорядочено.
Теорема 6. Полукольцо натуральных чисел линейно упорядочено.
Доказательство.
Следует из теоремы 6.
