
- •Федеральное агентство по образованию
- •Независимость аксиом Пеано.
- •Непротиворечивость системы аксиом Пеано.
- •Категоричность теории натуральных чисел.
- •Сложение натуральных чисел.
- •Свойства операции сложения на множестве натуральных чисел:
- •Умножение натуральных чисел.
- •Свойства операции умножения на множестве натуральных чисел:
- •Упорядоченность полукольца натуральных чисел.
- •Свойства отношения :
- •Понятия наибольшего и наименьшего элементов некоторого множества. Теоремы о существовании наибольшего и наименьшего элементов в подмножестве множества натуральных чисел.
- •Іі и ііі формы метода математической индукции для натуральных чисел.
- •Архимедовская расположенность полукольца натуральных чисел.
- •Лекции 3-4. Построение множества целых чисел.
- •Сложение и умножение целых чисел.
- •Кольцо целых чисел.
- •Вложение полукольца натуральных чисел в кольцо целых.
- •Строение кольца целых чисел.
- •Положительный конус и его свойства.
- •Свойства отношения :
- •Упорядоченность кольца целых чисел.
- •Три формы метода математической индукции для целых чисел.
- •Теоремы о существовании наибольшего и наименьшего элементов в подмножестве множества целых чисел.
- •Абсолютная величина целого числа и его свойства.
- •Свойства модуля:
- •Теорема о делении с остатком.
- •Архимедовская расположенность кольца целых чисел.
- •Лекции 5-6. Построение множества рациональных чисел.
- •Сложение и умножение рациональных чисел.
- •Поле рациональных чисел.
- •Вложение кольца целых чисел в поле рациональных.
- •Упорядоченность поля рациональных чисел.
- •Архимедовская расположенность поля рациональных чисел.
- •Лекция 7. Фундаментальные последовательности рациональных чисел и их свойства
- •Операции над последовательностями рациональных чисел.
- •Нулевые, положительные, отрицательные последовательности рациональных чисел.
- •Эквивалентные последовательности рациональных чисел и их свойства.
- •Лекции 8-9. Построение множества действительных чисел.
- •Поле действительных чисел.
- •Вложение поля рациональных чисел в поле действительных чисел.
- •Упорядоченность поля действительных чисел.
- •Архимедовская расположенность поля действительных чисел.
- •Теорема о сходимости любой фундаментальной последовательности рациональных чисел в поле действительных чисел.
- •Теорема о сходимости любой фундаментальной последовательности действительных чисел в поле действительных чисел.
- •Лекция 10. Поле комплексных чисел.
- •Алгебраическая форма записи комплексного числа.
- •Свойства сопряженных комплексных чисел:
- •Свойства нормы:
- •Геометрическая интерпретация комплексного числа. Тригонометрическая форма записи комплексного числа.
- •Корни - ой степени из единицы
- •Лекция 11. Тело кватернионов.
- •Алгебраическая форма кватернионов.
- •Свойства сопряженных и нормы.
- •Геометрическая интерпретация чисто мнимых кватернионов
- •Лекция 12. Ассоциативные алгебры.
- •Теорема Фробениуса.
- •Дуальные и двойные числа (ассоциативные алгебры над полем действительных чисел размерности 2).
- •Алгебра Кэли (Неассоциативная альтернативная алгебра с делением).
Алгебраическая форма записи комплексного числа.
![]() ,
,
где
![]() .
.
Определение.
![]() - алгебраическая форма записи комплексного
числа, причем единственная.
- алгебраическая форма записи комплексного
числа, причем единственная.
Предложение
1.
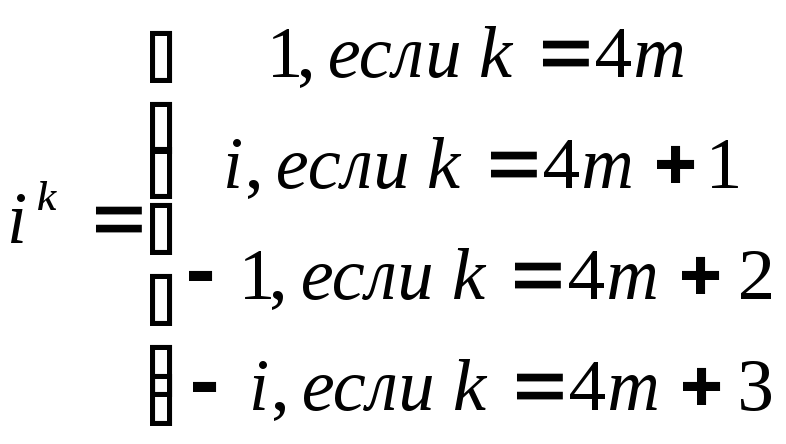 для любого
для любого![]() .
.
Определим действия сложения и умножения на множестве комплексных чисел, заданных в алгебраической форме:
![]()
![]()
Определение.
Сопряженным
к комплексному числу
![]() называется комплексное число
называется комплексное число![]() .
.
Свойства сопряженных комплексных чисел:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() т.т.т.,к.
т.т.т.,к.![]() ;
;
5.
![]() для любого
для любого![]() .
.
Определение.
Нормой
комплексного числа
![]() называется число
называется число![]() .
.
Замечание.
![]() .
.
Свойства нормы:
1.
![]() ;
;
2.
![]() т.т.т.,к.
т.т.т.,к.![]() ;
;
3.
![]() ;
;
4. если
![]() ,
то
,
то![]() .
.
Геометрическая интерпретация комплексного числа. Тригонометрическая форма записи комплексного числа.
Пусть
![]() .
.

Каждому комплексному
числу
![]() ставится в соответствие точка
ставится в соответствие точка![]() в прямоугольной системе координат.
в прямоугольной системе координат.
Если
![]() и
и![]() ,
то
,
то![]() .
При этом
.
При этом![]() .
.
Тригонометрическая
форма записи комплексного числа возникает
из геометрической интерпретации. Так,
каждой точке
![]() можно поставить в соответствие
радиус-вектор
можно поставить в соответствие
радиус-вектор![]() ,
который определяется длиной
,
который определяется длиной![]() и направлением – углом
и направлением – углом![]() отклонения
от положительного направления оси
отклонения
от положительного направления оси![]() .
.
Замечание.
![]() ,
,![]() ,
,![]() .
.
Таким образом
![]() .
Последняя запись и есть тригонометрическая
форма записи комплексного числа.
.
Последняя запись и есть тригонометрическая
форма записи комплексного числа.
Предложение
2. Если
![]() ,
то
,
то![]() для каждого
для каждого![]() .
.
Доказательство.
Пусть
![]() ,
,![]() .
Тогда
.
Тогда
![]() .
Последнее равенство и дает основание
утверждать справедливость данной
теоремы.
.
Последнее равенство и дает основание
утверждать справедливость данной
теоремы.
что и требовалось доказать.
Замечание.
![]() .
.
Корни - ой степени из единицы
Определение.
Комплексное число
![]() называется корнем
называется корнем![]() - ой степени из единицы, где
- ой степени из единицы, где![]() ,
если
,
если![]() .
.
Вычислим все корни
![]() - ой степени из единицы. Пусть
- ой степени из единицы. Пусть![]() .
Зная, что
.
Зная, что![]() ,
составим систему:
,
составим систему: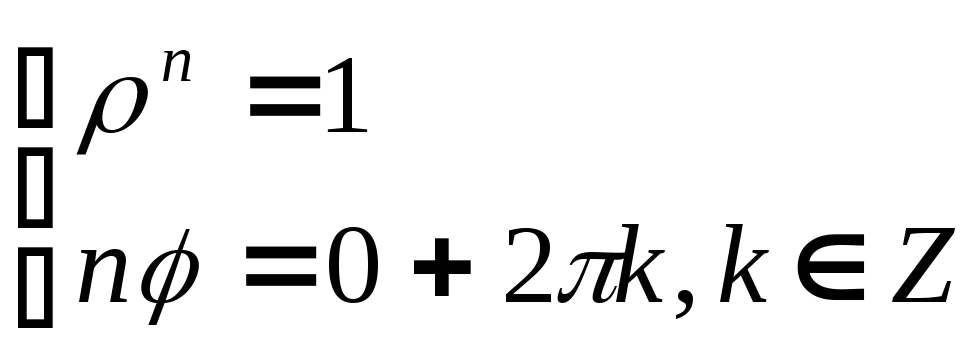 .
Тогда
.
Тогда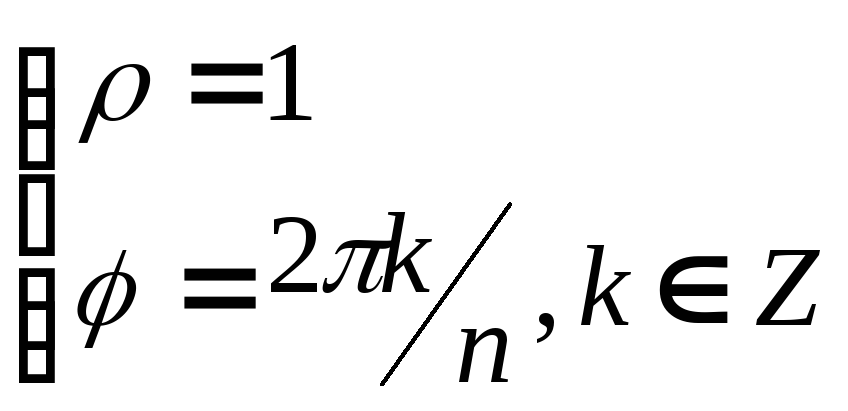 и любой корень
и любой корень![]() - ой степени из единицы будет иметь вид:
- ой степени из единицы будет иметь вид:![]() .
.
Покажем, что
существует ровно
![]() различных корней
различных корней![]() - ой степени из единицы. Для этого поделим
- ой степени из единицы. Для этого поделим![]() на
на![]() с остатком, получим
с остатком, получим![]() ,
где
,
где![]() .
Следовательно,
.
Следовательно,![]() .
Поскольку
.
Поскольку![]() может принимать только одно из
может принимать только одно из![]() значений
значений![]() ,
то и различных корней
,
то и различных корней![]() - ой степени из единицы также будет ровно
- ой степени из единицы также будет ровно![]() штук, причем
штук, причем![]() ,
где
,
где![]() .
.
Теорема
3.
Корни
![]() - ой степени из единицы образуют
мультипликативную циклическую группу.
- ой степени из единицы образуют
мультипликативную циклическую группу.
Доказательство.
Пусть
![]() - всех корней
- всех корней![]() - ой степени из единицы. Очевидно, что
- ой степени из единицы. Очевидно, что![]()
![]()
![]() .
Тогда
.
Тогда![]() замкнуто относительно умножения.
замкнуто относительно умножения.
Операция умножения
во множестве
![]() ассоциативна;
ассоциативна;![]() - нейтральный элемент в
- нейтральный элемент в![]() ;
;![]() .
.
Таким образом,
![]() группа, в которой элемент
группа, в которой элемент![]() является порождающим, так как
является порождающим, так как![]()
![]() ,
следовательно,
,
следовательно,![]() - мультипликативная циклическая группа.
- мультипликативная циклическая группа.
что и требовалось доказать.
Определение.
Комплексное число
![]() называется корнем
называется корнем![]() - ой степени из ненулевого комплексного
числа
- ой степени из ненулевого комплексного
числа![]() ,
где
,
где![]() ,
если
,
если![]() .
.
Вычислим все корни
![]() - ой степени из комплексного числа
- ой степени из комплексного числа![]() .
Пусть
.
Пусть![]() ,
,![]() .
Зная, что
.
Зная, что![]() ,
составим систему:
,
составим систему: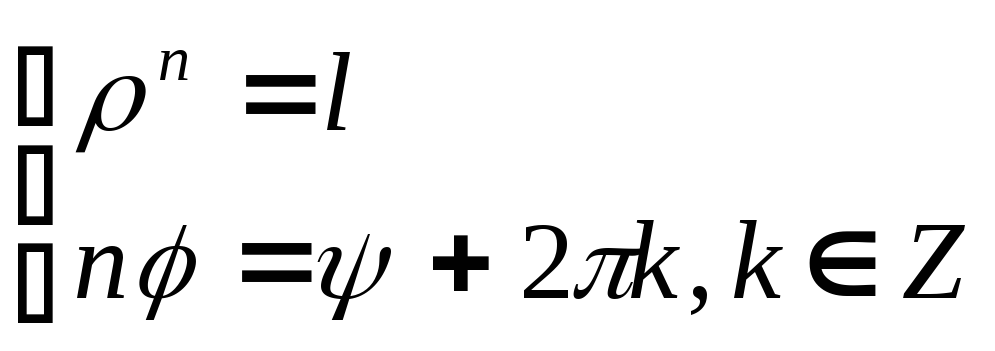 .
Тогда
.
Тогда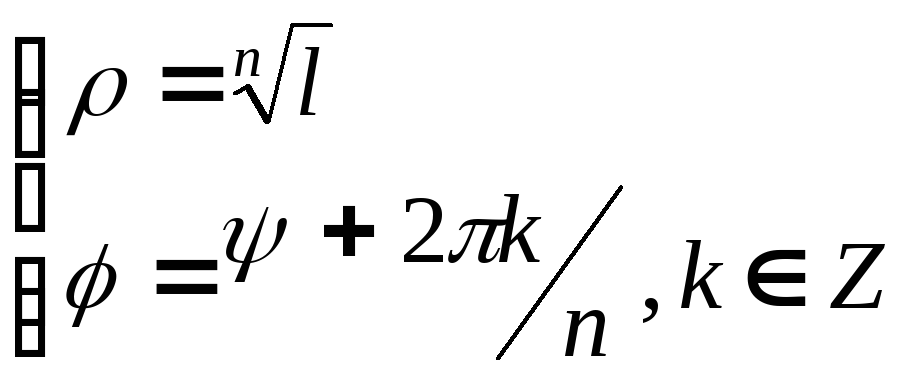 и любой корень
и любой корень![]() - ой степени из комплексного числа
- ой степени из комплексного числа![]() будет иметь вид:
будет иметь вид:![]() .
.
Покажем,
что существует ровно
![]() различных корней
различных корней![]() - ой степени из комплексного числа
- ой степени из комплексного числа![]() .
Для этого поделим
.
Для этого поделим![]() на
на![]() с остатком, получим
с остатком, получим![]() ,
где
,
где![]() .
Следовательно,
.
Следовательно,![]()
![]() .
Поскольку
.
Поскольку
![]() может принимать только одно из
может принимать только одно из![]() значений
значений![]() ,
то и различных корней
,
то и различных корней![]() - ой степени из комплексного числа
- ой степени из комплексного числа![]() также будет ровно
также будет ровно![]() штук, причем
штук, причем![]() ,
где
,
где![]() .
.
Замечание. Для
каждого
![]() справедливо
справедливо![]()
![]() .
.
Следствие.
Все корни
![]() - ой степени из ненулевого комплексного
числа
- ой степени из ненулевого комплексного
числа![]() являются результатом умножения одного
из этих корней на корни
являются результатом умножения одного
из этих корней на корни![]() - ой степени из единицы.
- ой степени из единицы.
Пример. Найти все корни 3 – ей степени из -8.
Очевидно, что -2 – один из искомых корней. Тогда, согласно вышеприведенному следствию,
![]() ,
,
![]() ,
,
![]() .
.
Теорема 5. Поле комплексных чисел не является упорядоченным.
Доказательство.
Предположим, что
![]() упорядоченное поле с положительным
конусом
упорядоченное поле с положительным
конусом![]() .
Согласно аксиомам положительного
конуса, для элемента
.
Согласно аксиомам положительного
конуса, для элемента![]() справедливо одно из следующих условий:
справедливо одно из следующих условий:
1.
![]() ,
что противоречит
,
что противоречит![]() ;
;
2.
![]() ,
что противоречит
,
что противоречит![]() ;
;
3.
![]() ,
что противоречит
,
что противоречит![]() .
.
Таким образом, ни
одно из трех условий не выполняется,
следовательно, предположение о
существовании положительного конуса
ложно, и, значит,
![]() не является упорядоченным полем.
не является упорядоченным полем.
что и требовалось доказать.
