
- •Федеральное агентство по образованию
- •Независимость аксиом Пеано.
- •Непротиворечивость системы аксиом Пеано.
- •Категоричность теории натуральных чисел.
- •Сложение натуральных чисел.
- •Свойства операции сложения на множестве натуральных чисел:
- •Умножение натуральных чисел.
- •Свойства операции умножения на множестве натуральных чисел:
- •Упорядоченность полукольца натуральных чисел.
- •Свойства отношения :
- •Понятия наибольшего и наименьшего элементов некоторого множества. Теоремы о существовании наибольшего и наименьшего элементов в подмножестве множества натуральных чисел.
- •Іі и ііі формы метода математической индукции для натуральных чисел.
- •Архимедовская расположенность полукольца натуральных чисел.
- •Лекции 3-4. Построение множества целых чисел.
- •Сложение и умножение целых чисел.
- •Кольцо целых чисел.
- •Вложение полукольца натуральных чисел в кольцо целых.
- •Строение кольца целых чисел.
- •Положительный конус и его свойства.
- •Свойства отношения :
- •Упорядоченность кольца целых чисел.
- •Три формы метода математической индукции для целых чисел.
- •Теоремы о существовании наибольшего и наименьшего элементов в подмножестве множества целых чисел.
- •Абсолютная величина целого числа и его свойства.
- •Свойства модуля:
- •Теорема о делении с остатком.
- •Архимедовская расположенность кольца целых чисел.
- •Лекции 5-6. Построение множества рациональных чисел.
- •Сложение и умножение рациональных чисел.
- •Поле рациональных чисел.
- •Вложение кольца целых чисел в поле рациональных.
- •Упорядоченность поля рациональных чисел.
- •Архимедовская расположенность поля рациональных чисел.
- •Лекция 7. Фундаментальные последовательности рациональных чисел и их свойства
- •Операции над последовательностями рациональных чисел.
- •Нулевые, положительные, отрицательные последовательности рациональных чисел.
- •Эквивалентные последовательности рациональных чисел и их свойства.
- •Лекции 8-9. Построение множества действительных чисел.
- •Поле действительных чисел.
- •Вложение поля рациональных чисел в поле действительных чисел.
- •Упорядоченность поля действительных чисел.
- •Архимедовская расположенность поля действительных чисел.
- •Теорема о сходимости любой фундаментальной последовательности рациональных чисел в поле действительных чисел.
- •Теорема о сходимости любой фундаментальной последовательности действительных чисел в поле действительных чисел.
- •Лекция 10. Поле комплексных чисел.
- •Алгебраическая форма записи комплексного числа.
- •Свойства сопряженных комплексных чисел:
- •Свойства нормы:
- •Геометрическая интерпретация комплексного числа. Тригонометрическая форма записи комплексного числа.
- •Корни - ой степени из единицы
- •Лекция 11. Тело кватернионов.
- •Алгебраическая форма кватернионов.
- •Свойства сопряженных и нормы.
- •Геометрическая интерпретация чисто мнимых кватернионов
- •Лекция 12. Ассоциативные алгебры.
- •Теорема Фробениуса.
- •Дуальные и двойные числа (ассоциативные алгебры над полем действительных чисел размерности 2).
- •Алгебра Кэли (Неассоциативная альтернативная алгебра с делением).
Операции над последовательностями рациональных чисел.
Определение.
Суммой последовательностей
![]() и
и![]() называется последовательность, полученная
в результате сложения соответствующих
членов этих последовательностей, т.е.
называется последовательность, полученная
в результате сложения соответствующих
членов этих последовательностей, т.е.![]() .
.
Определение.
Произведением последовательностей
![]() и
и![]() называется последовательность, полученная
в результате умножения соответствующих
членов этих последовательностей, т.е.
называется последовательность, полученная
в результате умножения соответствующих
членов этих последовательностей, т.е.![]() .
.
Замечание.
Разностью последовательностей
![]() и
и![]() является сумма последовательностей
является сумма последовательностей![]() и
и![]() .
.
Теорема 2. Сумма, произведение и разность сходящихся последовательностей рациональных чисел является сходящейся последовательностью.
Доказательство.
Поскольку предел суммы, произведения, разности сходящихся последовательностей равен соответственно сумме, произведению, разности пределов этих последовательностей, теорему можно считать доказанной.
что и требовалось доказать.
Свойство 4 ф.п.р.ч. Сумма, произведение и разность фундаментальных последовательностей рациональных чисел является фундаментальной последовательностью.
Доказательство.
Докажем теорему сначала для фундаментальных последовательностей.
Пусть
![]() и
и![]() - фундаментальные последовательности
рациональных чисел. Тогда
- фундаментальные последовательности
рациональных чисел. Тогда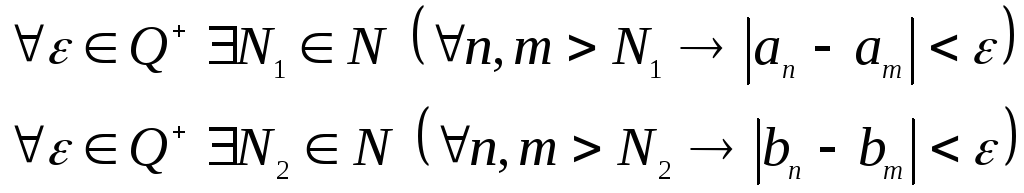 .
Полагая
.
Полагая![]() ,
получим
,
получим![]()
![]() ,
,![]() .
Оценим
.
Оценим![]() :
:
![]() .
.
Последнее неравенство
справедливо в силу свойства
3 ф.п.р.ч. оо
ограниченности любой ф.п.р.ч.. Следовательно,
последовательность
![]() является фундаментальной.
является фундаментальной.
Аналогично
устанавливается фундаментальность
последовательности![]() .
.
Последовательность
![]() фундаментальна,поскольку
фундаментальна,поскольку
![]() и всякая постоянная последовательность
рациональных чисел фундаментальна
и всякая постоянная последовательность
рациональных чисел фундаментальна![]() .
.![]() .
.
что и требовалось доказать
Определение.
Частным двух последовательностей
![]() и
и![]() при условии, что среди членов
последовательности
при условии, что среди членов
последовательности![]() отсутствуют числа, равные нулю, называется
последовательность
отсутствуют числа, равные нулю, называется
последовательность![]() .
.
Свойство 5
ф.п.р.ч.
Частным фундаментальных последовательностей
![]() и
и![]() рациональных чисел при условии, что
среди членов последовательности
рациональных чисел при условии, что
среди членов последовательности![]() отсутствуют числа, равные нулю, и
отсутствуют числа, равные нулю, и![]() не сходится к нулю, является фундаментальной
последовательностью рациональных
чисел.
не сходится к нулю, является фундаментальной
последовательностью рациональных
чисел.
Доказательство.
Поскольку
![]() не сходится к нулю, то найдется
положительное рациональное число
не сходится к нулю, то найдется
положительное рациональное число![]() и натуральное
и натуральное![]() такие, что
такие, что
![]() .
Поскольку последовательности
.
Поскольку последовательности![]() и
и![]() фундаментальны, имеем:
фундаментальны, имеем:
![]() - ограниченная,
следовательно,
- ограниченная,
следовательно,
![]() ;
;
![]() .
.
Выберем
![]() .
Тогда
.
Тогда
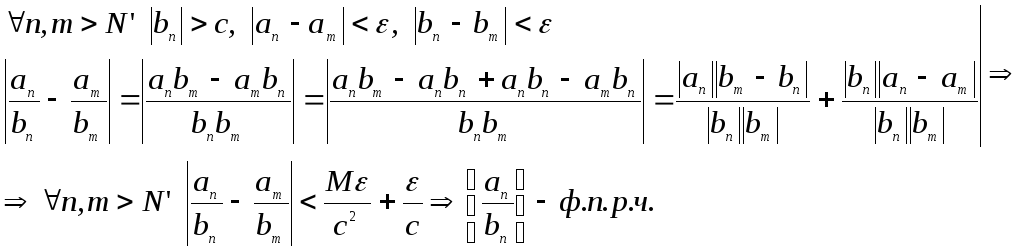
что и требовалось доказать
Нулевые, положительные, отрицательные последовательности рациональных чисел.
Определение. Последовательность рациональных чисел, сходящаяся к 0, называется нулевой последовательностью.
Следствия из определения:
Любая нулевая последовательность рациональных чисел является ф.п.р.ч.
Любая подпоследовательность нулевой последовательности является нулевой.
Произведение, сумма и разность нулевых последовательностей является нулевой.
Множество всех нулевых последовательностей образует подкольцо в кольце всех ф.п.р.ч.
Определение.
Последовательность
рациональных чисел
![]() называется положительной, если
называется положительной, если![]() .
.
Определение.
Последовательность
рациональных чисел
![]() называется отрицательной, если
называется отрицательной, если![]() будет положительной.
будет положительной.
Следствие. Любая подпоследовательность положительной (отрицательной) последовательности будет положительной.
Теорема 3. Сумма и произведение положительных последовательностей рациональных чисел является положительной последовательностью рациональных чисел.
Доказательство.
Пусть
![]() и
и![]() - положительные последовательности
рациональных чисел, что влечет
- положительные последовательности
рациональных чисел, что влечет
![]() .
.
Пусть
![]() .
Тогда
.
Тогда![]() .Последовательно
складывая и умножая последние неравенства,
получим
.Последовательно
складывая и умножая последние неравенства,
получим
![]() .
Поскольку
.
Поскольку![]() ,
а
,
а
![]() - произвольное, большее
- произвольное, большее![]() число, последовательности
число, последовательности![]() и
и![]() положительны.
положительны.
что и требовалось доказать
Теорема 4.
Если фундаментальные последовательности
![]() и
и![]() не являются положительными, тогда
фундаментальная последовательность
не являются положительными, тогда
фундаментальная последовательность![]() будет нулевой.
будет нулевой.
Доказательство.
По условию
![]() и
и![]() не являются положительными, следовательно,
не являются положительными, следовательно,![]() .
Учитывая фундаментальность
последовательностей
.
Учитывая фундаментальность
последовательностей![]() и
и![]() ,
можно выбрать
,
можно выбрать![]() настолько большим, чтобы выполнялись
неравенства:
настолько большим, чтобы выполнялись
неравенства:
![]()
Тогда
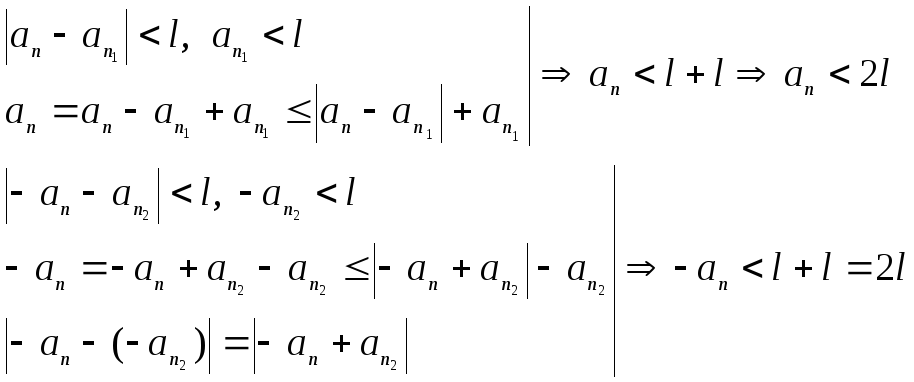
Выбрав
![]() ,
получим
,
получим![]() для сколь угодно малого
для сколь угодно малого![]() ,
а это возможно лишь в одном случае, если
,
а это возможно лишь в одном случае, если![]() является нулевой последовательностью
рациональных чисел.
является нулевой последовательностью
рациональных чисел.
что и требовалось доказать
Следствие.
Если
![]() - ф.п.р.ч., тогда либо
- ф.п.р.ч., тогда либо![]() положительна, либо
положительна, либо![]() положительна, либо
положительна, либо![]() -
нулевая.
-
нулевая.
