2.4 Аспекты, вызывающие сомнение в правомерности использования для оценки надежности условных вероятностей и условных плотностей вероятностей в математических моделях надежности агрегатов

Первый аспект. Целесообразно рассмотреть процедуры построения математических моделей, представленных экспоненциальным распределением, основанные на использовании условных вероятностей и условных плотностей вероятностей, которые применяются, как в учебной [37, 43], так и научной литературе [50].

Во многих отечественных источниках в области надежности, условная вероятность безотказной работы на отрезке времени [t_a; t_b], (t_b  t_a) определена как вероятность безотказной работы на момент t_b, при условии если до момента времени t_a отказа не было, и выражена как

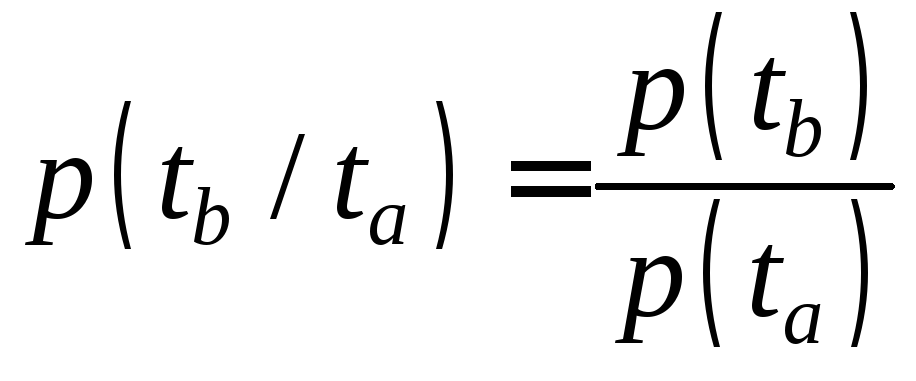. (2.19)

Но в приведенном виде формулировка не соответствует выражению (2.19), поскольку, если до момента t_a отказа не было, то на участке [0; ] вероятность безотказной работыp(t_a) = 1. В монографии [50] дана более корректная формулировка, в которой отсутствие отказа до момента времени t_a определено с некоторой вероятностью p(t_a).

Выражение (2.19) в соответствии с [37] получено из следующих соображений. Событие А определяет безотказную работу агрегата за время [0; t_a], а событие В – безотказную работу за [0; t_b]. Тогда вероятность совместного события А  В имеет вид

, (2.20)

т. е. равна произведению вероятности события А на условную вероятность события В при условии, что А произошло. В связи с этим, в [37] принято, что событие А поглощается событием В (т. е. если произошло событие В, то произошло и событие А). Следовательно, вместо (2.20) можно записать

. (2.21)

Переходя от событий ко времени и, получают

, (2.22)

или отсюда условную вероятность

. (2.23)

Однако, в теории вероятностей такой формулы нет, а в надежности она введена!

Некорректность приведенного из [37] рассуждения состоит в том, что события А и В приняты как определяющие безотказную работу за время от 0 до t_a и от 0 до t_b соответственно, но не определено с какими вероятностями. Выражение (2.21) получено в предположении, что произошло событие В и событие А. В случае если вероятность безотказной работы , то событиеВ не обязательно является поглощающим для события А. Но если имели место события безотказной работы при изменении времени от 0 до t_a и от 0 до t_b, то вероятности их реализации p(В) = p(А) = p(t_b) = p(t_a) = 1. Тогда, неясно, что обозначают выражения (2.21) – (2.23) и, причем здесь вероятности?

Второй аспект. Интегральная функция вероятности безотказной работы агрегата p(t), для которой определяется условная вероятность p(t_b /t_a) строится по результатам испытаний большой группы одинаковых агрегатов. Одни из них отказывают при меньших значениях времени, другие при больших. Время, при котором агрегаты отказывали, определяется только их собственными свойствами. Поэтому на количество и вероятность отказа агрегатов на отрезке t_a    t_b, не может повлиять количество и вероятность отказа агрегатов при t  t_a. В этом и состоит условие отсутствия последействия в потоке отказов вследствие независимости событий отказов агрегатов. Выполнение этого условия исключает возможность определения условных вероятностей.

Остановимся на этом подробнее. Как уже отмечалось ранее, в теории вероятностей [39, 47], вероятность реализации события на отрезке t_a    t_b, например, вероятность отказа, определена как приращение интегральной функции на этом отрезке в виде

. (2.24)

Это выражение также определенным образом учитывает условие реализации отказа на отрезке , поскольку учитывает возможность отказа при всех t  t_a с вероятностью q(t_a), но без нарушения условия отсутствия последействия.

Учитывая, что вероятность отказа q(t) = 1 – p(t), перепишем (2.24) в вероятностях безотказной работы

. (2.25)

Сравним значения вероятностей безотказной работы на отрезке , определенные по выражениям (2.23) и (2.25). Так как эти выражения справедливы для любых законов распределения вероятностей безотказной работы, то для простоты и наглядности примем в расчете распределение с равномерной плотностью вероятности при котором

. (2.26)

Подставив (2.26) в (2.25), выразим вероятность безотказной работы

, (2.27)

которая не зависит от положения отрезка  на оси времени t.

Применив (2.26) к (2.23), получим выражение

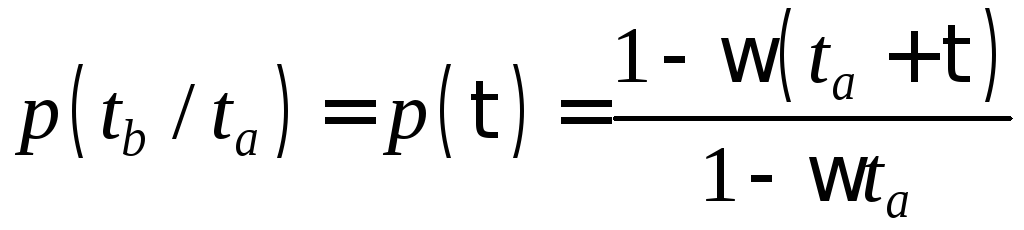. (2.28)

Рассмотрим конкретный пример для  = 0,1 и  = 1. Характер изменения показан на рис. 2.11.

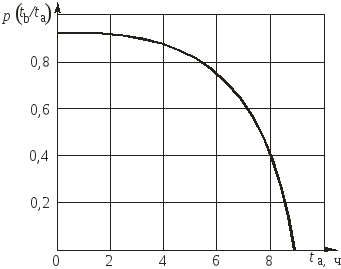
Рисунок 2.11 – Зависимость условной вероятности

безотказной работы от координаты начала

участка t_a при  = 0,1 и  = 1

Из этого рисунка следует, что условная вероятность безотказной работы на отрезке  фиксированной длины существенно нелинейна, что, при постоянной плотности вероятности отказа, представляется не оправданным.

Третий аспект. В традиционной теории надежности [43] особое значение отводится условной плотности вероятности отказов, которая определяется как плотность вероятности отказа в моменты времени t  t₁, при условии, что до момента t₁ отказа не было.

Рассмотрим рассуждения, определяющие правомерность условной плотности вероятности отказа, приведенные в [37]. Предполагается, что агрегат проработал время t₁, и в момент времени t₁ остался работоспособным, т. е. отказа нет с вероятностью равной единице (рис.2.12).

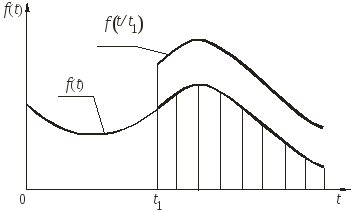
Рисунок 2.12 – Плотность вероятности и условная

плотность вероятности отказа агрегата.

За оставшееся время t  t₁ агрегат должен отказать, т. е. отказать с вероятностью равной единице. Следовательно, площадь под кривой плотности вероятности f(t), расположенная правее t₁, численно должна быть равна единице. Чтобы выполнялось это условие, все ординаты плотности f(t), лежащие правее t₁, авторами предложено разделить на нормирующее число, равное значению площади f(t) на интервале от t₁ до , т.е. само на себя.

Поскольку имеет место выражение

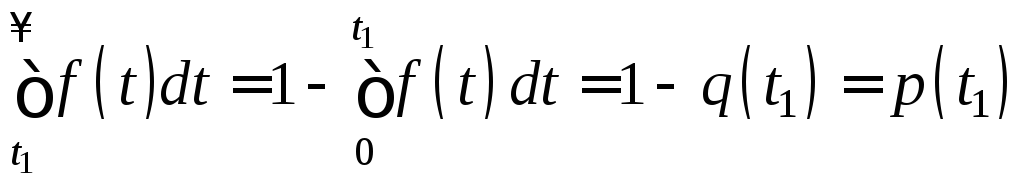,(2.29)

то условная плотность вероятности отказа в точке t₁ при условии, что до t₁ отказа небыло с вероятностью безотказной работы запишется как

.(2.30)

При построении условной плотности вероятности, в соответствии с рассмотренной процедурой, предложено ординаты правее точки t₁ увеличить, используя нормирующий множитель, определенный при условии, что до точки t₁ отказов не было с вероятностью равной единице. Но экспериментально построенная плотность вероятности содержит статистическую информацию о том, что до точки t₁ отказы были.

Возникает вопрос. На каком основании экспериментально построенная плотность вероятности подвергается трансформации, при которой до точки t₁ ее ординаты приравниваются к 0, а после t₁ увеличиваются посредством нормирующего множителя? Поставленный вопрос для теории надежности чрезвычайно важен, поскольку ответ на него определяет правомерность определения интенсивности отказов (t) и последующего построения математической модели вероятности безотказной работы агрегатов в виде экспоненциального распределения.

И наконец, если до момента времени отказа небыло с вероятностью равной 1, тои в соответствии с (2.17)

. (2.31)

В работе [50] введена другая трактовка выражения (2.17): «интенсивность отказа – условная мгновенная плотность вероятности отказа в момент времени t при условии, что до этого времени отказа небыло с вероятностью ».

Четвертый аспект. В теории вероятностей рассматриваются условные вероятности и условные плотности вероятностей, но только для функций двух и более зависимых случайных величин.

Рассмотрим правомерность введения условной плотности вероятности для функции одной переменной. В теории надежности условная плотность вероятности отказа представлена в виде (2.30). Ранее уже было отмечено, что известны две трактовки выражения (2.30):

- первая определяет f(t|t₁) при условии, что до точки t₁ отказа не было с вероятностью равной единице [37];

- в соответствии со второй до точки t₁ отказа не было с вероятностью p(t₁) [50].

Поскольку p(t₁) определяет вероятность на отрезке [0, t₁], то в соответствии с первой трактовкой будем иметь

p(t₁)=1 и f(t|t₁)=f(t). (2.32)

В соответствии со второй трактовкой вероятность отказа на отрезке [0, t₁] равна

, (2.33)

а после точки t₁, в общем виде на отрезке [t₁, ∞], она определится как

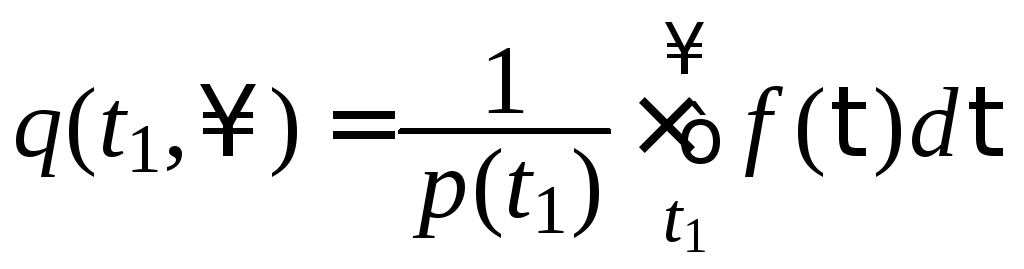(2.34)

Тогда вероятность отказа агрегата в диапазоне изменения времени работы от 0 до ∞ будет выражена как

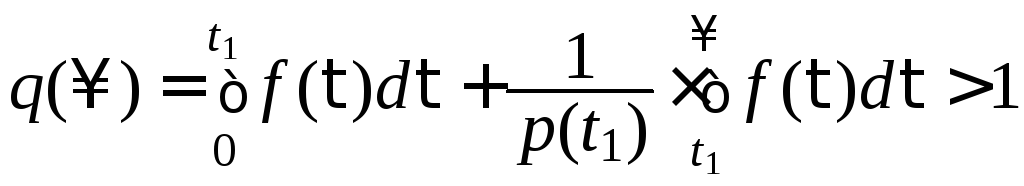. (2.35)

Значение вероятности отказа в возможном диапазоне изменения времени получено больше 1, поскольку сомножитель во втором члене 1/p(t₁) может быть только больше единицы. Из приведенного следует, что введение в рассмотрение условной плотности вероятности (2.30) не правомерно с позиции теории вероятностей, поскольку интеграл от плотности становится больше 1.

Кроме того, плотность вероятности отказа f(t) элемента строится по результатам испытаний большой группы таких элементов. Но отказ любого из них не зависит от отказов других испытуемых, т.е. события отказов элементов независимы. И введение условной плотности вероятности, даже из-за желания определения интенсивности отказов в форме (2.17) недопустимо с позиций основ испытания на надежность.

Против определения условной плотности вероятности отказа в форме (2.30) следует высказать ряд возражений:

– во-первых, рассматривается вероятностная задача (в вероятностной трактовке) и в ней по определяющей функции (вероятности отказа) дается детерминистическая трактовка. Предполагается, что при всех t  t₁, отказа не было с вероятностью равной единице, а положение t₁ на оси времени никак не ограничено (t₁ текущее значение времени);

– во-вторых, плотность вероятности отказа для отдельного агрегата определяется из статистики испытаний большой группы таких агрегатов и является распределением, ординаты которого определены из опыта и не подлежат изменению даже при необходимости формирования условной плотности;

– в-третьих, как и при определении условной вероятности безотказной работы, проигнорирован принцип отсутствия последействия;

– в-четвертых, в теории вероятностей [39] определение условных вероятностей и условных плотностей вероятностей предусматривает наличие системы двух зависимых случайных величин.

Пятый аспект. В работе [50] отмечается, что выражение (2.17) получено из рассмотрения результатов испытания совокупности не восстанавливаемых объектов, когда в процессе испытаний число исправных объектов убывает. Если ту же совокупность объектов испытывать по плану восстанавливаемых объектов, то по истечении некоторого промежутка времени поток отказов станет стационарным пуассоновским. Поскольку испытания проводятся с целью построения математической модели надежности отдельного агрегата, то к интерпретации их результатов следует подходить с предельной аккуратностью.

Покажем это. Обратим внимание на то, что экспоненциальное распределение (2.1) в котором , получено из выражения (2.17) в котором. Такой переход откчрезвычайно ответственен в смысле правомерности математической модели надежности элементов. Выражение (2.17) получено при испытании совокупности невосстанавливаемых объектов. Вывод выражения (2.1) как экспоненциальной математической модели вероятности безотказной работы из литературы неизвестен. Из выражения (2.17) получают не экспоненциальное, а показательное распределение (2.18) [37].

Там же в [37] отмечается, что реализуется при испытаниях совокупности однотипных элементов по плану с восстановлением. И в этой же работе предложено заменить в выражении (2.18)на, и получить, тем самым, из (2.18) выражение (2.1). Но такое преобразование некорректно, поскольку предлагается использовать модель, полученную при испытаниях совокупности элементов по плану без восстановления, для моделирования надежности элементов испытываемых по плану с восстановлением.

К тому же плотность вероятности отказа в соответствии с (2.1) и (2.2) имеет вид

. (2.36)

Здесь первый сомножитель является значением плотностипри, а второй сомножитель определяет процесс измененияво времени, свойственный экспоненциальному распределению. Утверждение о независимости интенсивности отказовот времени, при испытании совокупности восстанавливаемых объектов, равносильно утверждению о независимости от времени плотности вероятности. Посколькупри этом равна параметру потока отказов ω, а тот в свое время есть не что иное как математическое ожидание числа отказов в единицу времени, то в этом случаене может быть функцией времени.

Следовательно, в качестве закона распределения вероятности отказа элемента естественно принять не экспоненциальное распределение, полученное вследствие неправомерного преобразования выражения (2.18), а распределение равномерной плотности

. (2.37)

Приведенные доводы дают достаточно оснований сомневаться в возможности использования экспоненциальной модели для оценки надежности агрегатов.

Шестой аспект. В работах [50, 51] отмечается, что:«… в случае, когда отказы происходят в случайные моменты времени, и среднее число отказов на равных отрезках времени не зависит от их положения на оси времени, надежность устройства определяется хорошо известной экспоненциальной зависимостью (2.1)». Это утверждение исключает возможность определения условной плотности вероятности в виде выражения (2.30) и (2.17) из которого экспоненциальное распределение и получено. Вместе с этим, очевидно, что независимость числа отказов от положения отрезка на оси времени указывает на тот факт, что отказы распределены с равномерной плотностью вероятности.

Из выражения (2.17) после замены в нем f(t) на , разделения переменных и интегрирования, получают показательное распределение вероятности безотказной работы (2.18)

.

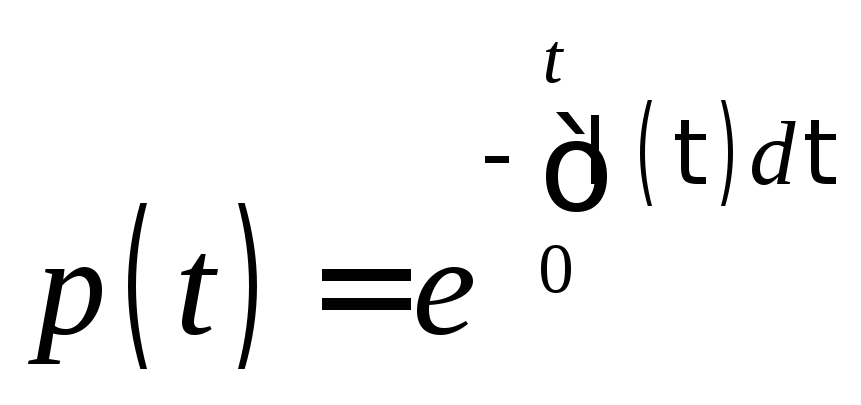Предполагается, что в случае стационарного процесса  = const, выражение (2.18) приобретает вид экспоненциального распределения (2.1)

Поскольку в исходном выражении (2.17) ограничения на вид функций f(t) и p(t) не наложены, то при произвольных законах распределения f(t) и p(t), интенсивность (t) постоянной быть не может.

Выражение (2.17) обращается в тождество (t) = , только при подстановке p(t) в виде (2.1) и f(t) в виде производной от нее. Но это и естественно, поскольку (2.1) получено из (2.17).

При замене в (2.18) () на (2.17) и использовании в (2.17)

распределения с равномерной плотностью вероятности, найдем

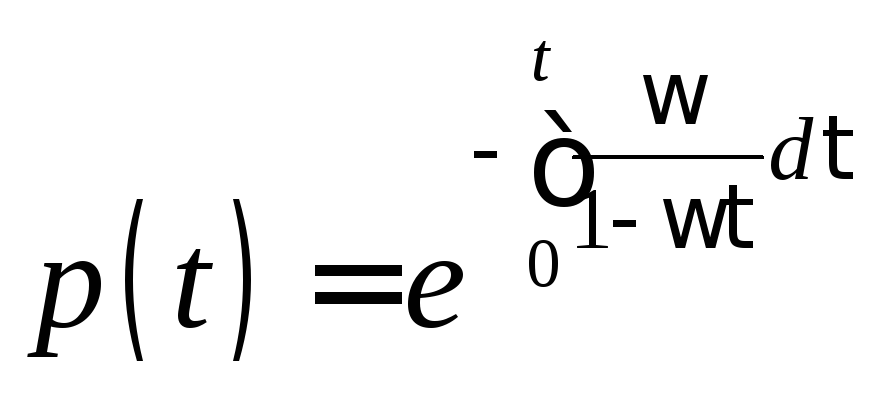. (2.38)

Результаты расчета p(t), выполненные по выражению (2.38), (показаны пунктирной линией), и по интегральной функции вероятности безотказной, соответствующей распределению с равномерной плотностью p(t) = 1 – t, при  = 0,1, приведены на рис. 2.13.

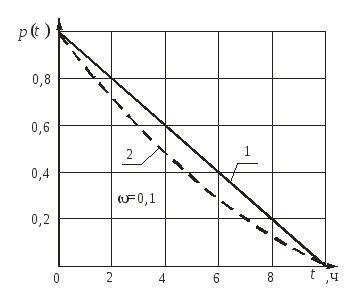
1. p(t) = 1 – t;

2.

Рисунок 2.13 – Вероятности безотказной работы

Расхождения результатов совершенно очевидны.

Таким образом, подводя итоги, можно сделать очевидные выводы, что получение модели надежности в виде экспоненциального распределения из представления интенсивности отказов как условной мгновенной плотности вероятности в виде

неправомерно, т.к.:

– в теории вероятностей условные вероятности и условные плотности вероятностей рассматриваются только для функций двух и более зависимых случайных величин;

– в теории надежности условие отсутствия последействия исключает возможность определения условных вероятностей и условных плотностей вероятностей;

– из исходного выражения для в теории надежности получено не экспоненциальное, а показательное распределение вероятности безотказной работы. Затем экспоненциальное распределение получено из показательного путем замены=var на =const. Такая замена не правомерна, поскольку =var и =const реализуются при различных планах испытаний, которым на практике соответствуют различные стратегии эксплуатации;

– в теории надежности показательная и экспоненциальная зависимости вероятности безотказной работы рассматриваются как функции распределения вероятности хотя они не удовлетворяют ограничениям, накладываемым в теории вероятностей на функции распределения вероятности.

Седьмой аспект. В ряде источников [8] отмечается, что использование в надежности экспоненциального распределения обосновано применением методов марковских процессов и уравнений Колмогорова к простейшим графам состояний невосстанавливаемых нерезервированных агрегатов. Рассматривается простейшая система состояний и переходов приведенная на рис. 2.14.

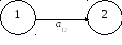
1 – исправное состояние;

2 – неисправное состояние.

Рис. 2.14 – Граф состояний необслуживаемых

нерезервированных агрегатов

Поскольку рассматривается процесс эксплуатации невосстанавливаемого агрегата, то в системе (рис. 2.14) будет иметь место только один переход 1-2. Поведение такой системы предлагается описать следующей системой дифференциальных уравнений Колмогорова:

(2.39)

.

Интенсивность перехода по своей физической сущности представляет собой интенсивность отказов необслуживаемых агрегатов λ. Используя преобразование Лапласа от системы дифференциальных уравнений (2.39) переходят к системе алгебраических уравнений

;

,

из которой найдено выражение для P₁(S)

.

Перейдя к оригиналу, с учетом начального условия , окончательно получено

(2.40)

Рассматриваемое решение содержит существенную некорректность в постановочной части. Марковские процессы, как и пуассоновские описывают системы и процессы, удовлетворяющие условию стационарности. Граф состояний (рис. 2.14) имеет только один переход, по завершении которого процесс функционирования заканчивается, т.е. рассматриваемая система не удовлетворяет условию стационарности.

Условие стационарности выполняется если в графе имеется замкнутый маршрут, в рассматриваемом случае если бы имелся обратный переход 2-1, как на рисунке 2.15.

Рис. 2.15 – Граф состояний и переходов нерезервированных восстанавливаемых (обслуживаемых) агрегатов.

Здесь интенсивность перехода 2-1

это интенсивность восстановления отказа, где Т_ср – среднее время восстановления.

Система дифференциальных уравнений для этой модели будет иметь вид:

;

,

Решение этой системы для вероятности нахождения агрегата в исправном состоянии , с использованием преобразований Лапласа (при условии), имеет вид

. (2.41)

Первый член суммы определяет при стационарном процессе, а второй член описывает переходный процесс от начального условия, до стационарного состояния вероятности.

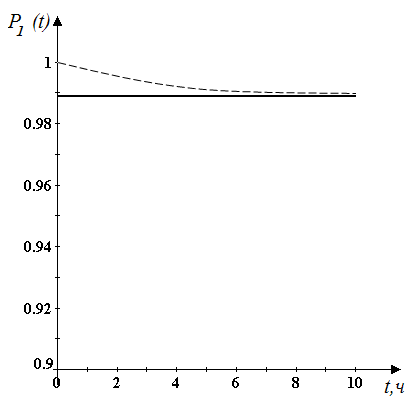
Графически состояние системы показано на рис. 2.16, при 1/ч и1/ч.

переходный процесс

стационарный процесс

Рисунок 2.16 – Зависимость вероятности нахождения системы

в исправном состоянии

Из приведенных результатов следует независимость стационарной части решения от времени, т.е. вероятность нахождения агрегата в исправном состоянии при стационарном процессе не моделируется экспоненциальной функцией времени. Экспоненциальной моделью представляется переходный процесс от значения до. Экспоненциальная же модель надежности агрегата предполагает изменение вероятности нахождения в исправном состояниив диапазоне от 1 до 0.

***

Приведенные рассуждения дают серьезные основания для сомнений как в правомерности построения экспоненциальной модели надежности агрегатов, так и в возможности ее использования в расчетах надежности сложных функциональных систем. А также убеждают в неправомерности использования условных вероятностей и условных плотностей вероятностей в математической модели надежности агрегатов.

В работе уделено большое внимание исследованию правомерности использования в расчетах надежности экспоненциального распределения поскольку во многих источниках [37, 43, 47] оно воспринимается в качестве основного закона расчета надежности агрегатов (элементов) систем.