39. Теорема Хинчина. Понятие об усиленном збч.

\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

В действительности требования конечности дисперсии в ЗБЧ для независимых одинаково распределенных с.в. связано исключительно со способом доказательства и на самом деле это утверждение остается справедлвым и без предположения конечности дисперсии.

Теорема Хинчина. Любая последовательностьнезависимых одинаково распределенных с.в., имеющих конечное МО, подчиняется ЗБЧ, т.е.

.

Доказательство:

Т.к. сходимость по вероятности к константе эквивалентна слабой сходимости (см. Лемму), то достаточно доказать слабую сходимость.

В соответствии с теоремой о непрерывности эта сходимость имеет место, если ил тоько если ХФ

Вычислим ХФ .

Так как МО существует и равно, то ХФможно разложить в ряд Тейлора в окрестности точки 0.

.

Следовательно, ХФ

При , используя замечательный предел, получаем:

На самом деле в условии теоремы Хинчина имеет место сходимость не только по вероятности, но и почти наверное.

Теорема Колмогорова(Усиленный ЗБЧ)

Если – последовательность независимых одинаково распределенных с.в., имеющих конечное МО, то

Центральная предельная теорема. (ЦПТ)

Пусть – последовательность независимых одинаково распределенных с.в., имеющих конечное МО и дисперсии

Пусть . Тогда в соответствии с ЗБЧ

или, в соответствии со свойствами сходимости по вероятности:

Возникает вопрос:

При делении на в пределе получается 0. Нельзя ли поделить на что-то, возрастающее кмедленнее, чем, чтобы предел не был равен нулю.

Оказывается, что уже к нулю не стремится, при этомстановится все более похоже на нормальный ЗР, т.е. имее место слабая сходимость последовательности ФР с.в.:

к ФР нормального закона.

Это и есть смысл ЦПТ.

\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

40. Статистическая модель. Генеральная совокупность (гс), выборка, объем выборки. Простейшие способы представления статистических данных.

\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Вероятностная модель случайных явлений основана на понятии вероятностного пространства . При этом в каждой конкретной ситуации вероятностьсчитается полностью известной числовой функцией на-алгебре, т.е.считается известной. Задача теории вероятностей состоит в том, чтобы находить вероятности сложных событий через известные вероятности простых событий. Однако на практике вероятностькак правило неизвестна. Можно только предположить, что истинная вероятностьявляется элементом некоторого класса вероятностей, допустимых для описания данного случайного явления.

Тройка – статистическая модель.

Цель математической статистики в общем случае – уточнение вероятностной модели случайного явления, т.е. отыскание истинной вероятности или близкой к ней, основываясь на наблюдаемых результатах эксперимента, называемых статистическими данными.

В классической МС имеют дело со случайными экспериментами, состоящими в проведении повторных независимых наблюдений над с.в., имеющей неизвестное распределение вероятностей, т.е. имеющей неизвестную.

В этом случае множество всех возможных значений с.в.называют генеральной совокупностью.

Числа ,,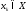являющиеся результатомнезависимых наблюдений над с.в., называют выборкой из генеральной совокупности,– объемом выборки.

Задача математической статистики: как по выборке из генеральной совокупности, иеющей ФР , извлекая из нее максимум информации, сделать обоснованные статистические выводы о неизвестных вероятностных характеристиках с.в..

Замечание. Обосновать качество статистических выводов на основе одной конкретной выборки принципиально нельзя. Выборка – это чисел, случайно отобранных из генеральной совокупности. И то, что верно для одной выборки, может оказаться неверным для другой.

Поэтому при рассмотрении теоретических вопросов и задач, когда необходимо получить результат, справедливый для любой выборки, на выборку следует смотреть как на случайный вектор , у которого все координатынезависимы и распределены так же, как и с.в..

В этом случае – копии с.в.. Т.е. смотреть на выборку априорно на случайный вектор, который еще не принял своего конкретного значения.

Под статистической моделью, отвечающей повторным неизменным наблюдениям над с.в. 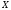, понимают тройку, где:

– генеральная совокупность,

– борелевская-алгебра подмножеств,

– класс допустимых функций распределения для с.в., к которому принадлежит и истинная неизвестная ФР .

Если ФР из класса заданы с точностью до значений параметра, принимающего значения множества(т.е.), то статистическую модель называют параметрической. При этом говорят, что известен тип распределения наблюдаемой с.в., а неизвестен только параметр, от которого распределение зависит.может быть как скаляром, так и вектором.

Статистические модели бывают непрерывными (НСВ) и дискретными (ДСМ), в соответствии с тем, какой является наблюдаемая с.в.

Примернепрерывной параметрической модели.

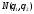– общая параметрическая нормальная модель. Наблюдаемая с.в.имеет нормальный ЗР с неизвестными.

.

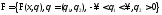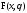имеют плотности вероятностей

Примердискретной параметрической модели:

– дискретная с.в., имеющая пуассоновский ЗР с неизвестным параметром.

:,

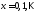
Задачи, решаемые в математической статистике, можно разбить на две большие группы:

1) Задачи, связанные с определением неизвестного ЗР наблюдаемой с.в. и параметров в него входящих. Задачи решаются в рамках теории оценивания.

2) Задачи, связанные с проверкой гипотез относительно ЗР наблюдаемой с.в.. Решаются в рамках теории проверки статистических гипотез.