4.1.1.1. Решение методом разделения переменных.

Одним из наиболее распространенных классических методов решения линейных краевых задач теплопроводности является так называемый метод разделения переменных Фурье. Основная идея этого метода заключается в сведении дифференциального уравнения в частных производных, каковым является уравнение теплопроводности, к дифференциальным уравнениям в обыкновенных производных, методы решения которых хорошо разработаны.

Для этого отыскивается некоторое частное решение линейного дифференциального уравнения теплопроводности

, (4.10)

где - избыточная температура, а t_f – температура среды, окружающей тело (t_f=const).

Частное решение ищется в виде произведения двух функций, одна из которых φ(τ) зависит только от времени, а другая ψ (x,y,z) является функцией только координат:

(4.11)

Подставив уравнение 4.11 в уравнение 4.10, получим

(4.12)

Левая часть выражения 4.12 зависит только от τ, правая – только от координат x,y,z . Равенство 4.12 возможно только в том случае, если левая и правая части равны некоторой постоянной λ = const (не путать с коэффициентом теплопроводности λ!).

(4.13)

Из равенства 4.13 получаем два дифференциальных уравнения:

(4.14)

(4.15)

Дифференциальное уравнение 4.14 является уже уравнением в обыкновенных производных. Применением метода разделения переменных и уравнение 4.15 также удается привести к трем дифференциальным уравнениям в обыкновенных производных.

Решение уравнения 4.14 находится достаточно просто в виде:

(4.16)

Введенная нами выше величина λ выбирается из физических соображений. Для процессов, стремящихся к состоянию температурного равновесия, λ<0, так как если принять λ>0, то при стремлении τ→ ∞ температура возрастала бы бесконечно. Чтобы подчеркнуть постоянство знака λ принимают условие λ = - k², тогда при любом k λ<0.

Для циклического изменения температур накладывают еще одно условие λ=ik². Тогда с учетом того, что по формуле Эйлера получаем периодический закон.

Подставив в уравнение 4.15 условие λ = - k², получим

(4.17)

Это уравнение называют уравнением Покеля, а решение задачи с учетом граничных условий называют задачей Штурма-Лиувилля.

Уравнение 4.17 имеет тривиальное решение ψ=0 при любых λ = k². Нетривиальные решения уравнения 4.17 имеют место не при любых числах λ, а при некоторых вполне определенных значениях λ₁, λ₂, ... и т.д.

Те числа λ, при которых имеются нетривиальные решения уравнения 4.17, носят название собственных значений дифференциального оператора ²+k² =0 или собственных чисел, а функции ψ, удовлетворяющие 4.17 при данных λ₁, λ₂, ... и т.д. , называют собственными функциями.

Уравнение 4.17

с помощью метода разделения переменных может быть приведено к трем дифференциальным уравнениям в обыкновенных производных следующим образом. Положим

(4.18)

Подставив 4.18 в 4.17, получим

(4.19)

Поделив левую и правую части уравнения 4.19 на ψ = XYZ, после перегруппировки получим

(4.20)

Левая часть уравнения 4.20 зависит только от х , а правая только от y и z ; это может быть только в том случае, если левая и правая части 4.20 равны некоторой постоянной разделения – l², не зависящей ни от х, ни от y и z. Поэтому

(4.21)

(4.22)

Тогда вместо уравнения 4.17 получаем следующие дифференциальные уравнения в обыкновенных производных:

; (4.23)

; (4.24)

(4.25)

где , откуда .

Получив решение уравнений 4.16 и 4.17 при каком-то конкретном значении собственного числа λ_n , мы получим одно из частных решений

(4.26)

Это решение удовлетворяет дифференциальному уравнению теплопроводности 4.10 и соответствующим граничным условиям, но не удовлетворяют начальным условиям.

Затем, пользуясь линейностью уравнения, решение задачи находят как линейную суперпозицию этих частных решений:

, причем такую, которая удовлетворяет уже и начальным условиям путем соответствующего подбора коэффициентов C_n.

Рассмотрим конкретный пример.

Пусть, например, требуется найти температурное поле в тонком изолированном по боковой поверхности стержне, расположенном вдоль оси х, если избыточная температура его концов нулевая, а начальное распределение температур есть некоторая функция f(х).

Математически такая задача формулируется следующим образом:

; (4.27)

τ =0 (4.28)

х=0 (4.29)

х=ℓ (4.30)

Следуя методу разделения переменных, частное решение будем искать в виде

(4.31)

Подставляя 4.31 в 4.27 , получим

(4.32)

Получим два дифференциальных уравнения в обыкновенных производных:

(4.33)

(4.34)

Общее решение 4.33 будет

(4.35)

а общее решение 4.34 имеет вид

(4.36)

Правильность решений легко проверить дифференцированием и сравнением с исходными уравнениями 4.33 и 4.34.

Постоянные С₂ и С₃ найдем из граничных условий 4.29 и 4.30. Используя 4.29, получим , откуда С₂=0 и решение 4.36 имеет вид

(4.37)

Используя граничное условие 4.30, имеем

(4.38)

Так как С₃ не может равняться 0 (иначе получается тривиальное решение, не представляющее интереса), то следует принять, что

, (4.39)

откуда видно, что k может принимать лишь ряд дискретных значений:

(4.40)

Тогда, подставляя (4.40) в 4.35 и 4.36, приходим к следующим выражениям

(4.41)

(4.42)

В свою очередь, подставляя 4.41 и 4.42 в 4.31, для частного решения получаем

, (4.43)

где С_n=С₁С₃

В начальный момент при τ = 0

(4.44)

Очевидно, что в общем случае правая часть соотношения 4.44 не равна f(х) и никаким подбором С_n подобного равенства достичь нельзя. Однако, если составить бесконечный ряд, сумма которого будет суммой частных решений

, (4.45)

то при условии, что этот ряд сходится и его можно дифференцировать, он тоже окажется решением дифференциального уравнения 4.27 , удовлетворяющим граничным условиям 4.29 и 4.30.

Для того, чтобы решение 4.45 удовлетворяло также начальному условию 4.28, необходимо, чтобы имело место равенство

(4.46)

Соотношение 4.46 есть разложение функции f(х) в ряд Фурье по синусам.

Если f(х) удовлетворяет известным условиям разложимости в ряд Фурье [9] , то коэффициенты этого ряда определятся по формуле

(4.47)

Тогда, подставляя С_n из формулы 4.47 в выражение 4.45, мы получаем окончательное решение поставленной задачи.

В учебных целях разработано методическое указание по расчету температур тел простейших геометрических форм для процесса остывания (охлаждения) их.

Одномерное тело (бесконечные пластина и цилиндр, шар) с одинаковой температурой во всех точках, равной t^/_, в начальный момент времени τ₀ погружается в жидкость с неизменной температурой t_ж . Коэффициент теплоотдачи на поверхности тела (для пластины с обеих боковых сторон) одинаков и постоянен.

Если за начало отсчета температуры принять температуру окружающей среды t_ж и избыточную температуру стенки обозначить то дифференциальное уравнение теплопроводности для твердых тел:

(1)

принимает вид

Граничные условия: при х = δ

Начальное условие: при τ = 0

При этом температуры тела на поверхности t_с и в плоскости симметрии t₀ для любого момента времени определяются из следующих соотношений:

и

где t^/ - начальная температура по всему сечению тела.

Пример распределения температур по толщине плоской стенки во времени

Рис. 1. Изменение температурного поля в плоской неограниченной стенке

от времени при охлаждении.

Безразмерная температура тела определяется безразмерной координатой , числом Био и числом Фурье , где х- текущая координата в направлении теплового потока, м; ℓ-характерный линейный размер тела, м; λ – коэффициент теплопроводности, Вт/м·К и а = - коэффициент температуропроводности материала тела, м²/с.

Аналитическое решение уравнения теплопроводности при заданных начальных и граничных условиях запишется:

(2)

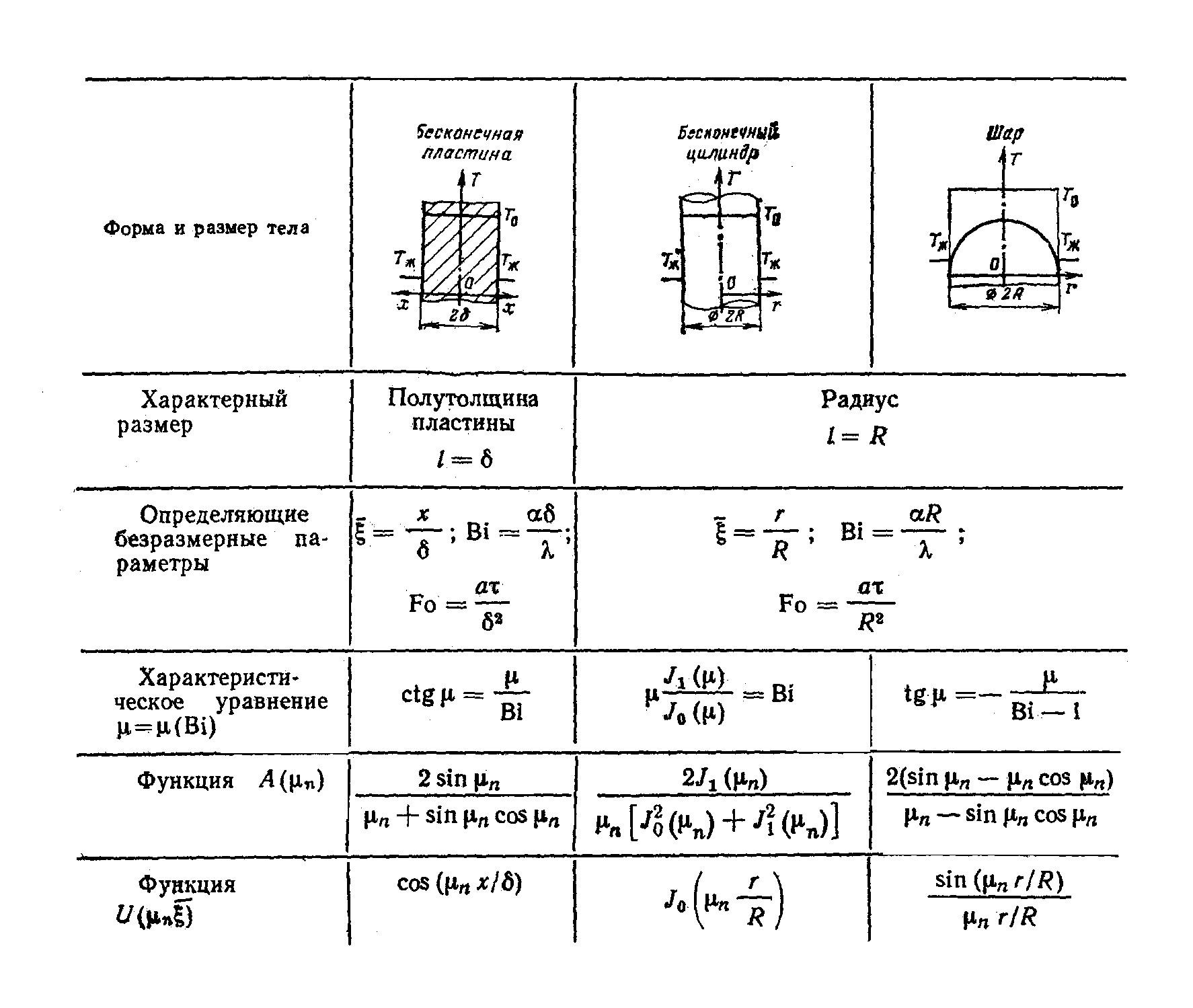
Здесь А и U – некоторые функции от корней характеристических уравнений μ_n, а сами корни являются однозначной функцией критерия Био.

В таблице 1 приведены: вид характеристических уравнений и соотношения для расчета функций А(μ_n) и для случая охлаждения (нагрева) бесконечной пластины, бесконечного цилиндра и шара. Через J₀ и J₁ обозначены функции Бесселя первого рода нулевого и первого порядка (функции приведены в табл.2). Начало координат расположено на средней плоскости для пластины, на оси для цилиндра и в центре для шара. Решение (2) может быть использовано для бесконечной пластины в случае, если одна из боковых плоскостей имеет абсолютную теплоизоляцию. В этом случае начало координат необходимо поместить на теплоизолированной стенке и в качестве характерного размера принять всю толщину стенки 2δ.

Первые шесть корней характеристических уравнений из таблицы 1 приведены в таблицах №№ 2 – 5.

При Fo>0,3 ряд (2) оказывается настолько быстро сходящимся, что для практических целей достаточно ограничиться первым членом (с погрешностью не выше 1%).

(3)

Таблица 1.

Так для плоской пластины общий вид решения

(3а)

а для практических целей решение записывается

(3^/а)

Здесь , , ,

Координата точки О на оси х расположена на расстоянии λ_ст/α_ж , м.

Как видно, даже для простейшего одномерного случая плоской или цилиндрической стенки решение задачи достаточно громоздкое и трудоемкое. Для тел произвольной формы и произвольного набора ГУ аналитического решения не существует. Безразмерная функция температур тел классической формы описывается критериями подобия:

= Bi - критерий Био;

= Fo – критерий Фурье.

На основании второй теоремы подобия искомая функция в виде безразмерной температуры в различных сходственных точках x/l =L может быть представлена в виде зависимости:

(4.50)

Здесь безразмерная форма температуры представляет из себя следующее:

, где

t_ж - температура окружающей среды;

t_с и - абсолютная и относительная температуры стенки;

t^/ и - абсолютная и относительные температуры стенки при τ = 0 (заданы начальными условиями).

При решении технических задач в большинстве случаев достаточно знать температуру на поверхности и в средней плоскости стенки . Выражение 4.50 упрощается, т.к. аргумент ξ становится постоянным числом (при х=0 ξ =0, а при х = δ ξ =1) и выпадает, как параметр.

Графическое изображение безразмерной наружной температуры плоской неограниченной пластины приведено на рис.4.5.

Рис.4.5. Зависимость безразмерной наружной температуры пластины от Bi и Fo.

Рис. 4.6. Зависимость безразмерной средней температуры пластины от Bi и Fo.

Рис. 4.7. Зависимость теплового потока через плоскую пластину от Bi и Fo.

Рис. 4.8. Зависимость наружной температуры цилиндра от Bi и Fo

Рис. 4.9. Зависимость внутренней температуры цилиндра от Bi и Fo.

Рис. 4.10. Зависимость теплового потока через цилиндр от Bi и Fo.

Рис. 4.11. Зависимость наружной температуры шара от Bi и Fo

Рис.4.12. Зависимость температуры в центре шара от Bi и Fo.

Рис. 4.13. Зависимость теплового потока внутрь шара от Bi и Fo.

При решении стационарных задач можно использовать принцип суперпозиции температурных полей.

Например, при решении уравнения Лапласа при граничных условиях третьего рода

; на границе Sj (4.51)

Решение можно представить как сумму решений вспомогательных задач

где T_k – решение вспомогательных задач:

, (4.52)

где ; ; - дельта-функция.

Графическая интерпретация получения решения методом суперпозиции:

Рис.4.14. Суперпозиция температурных двумерных полей.

Зависимость процесса распространения тепла от формы и размеров тела.

Скорость протекания процесса для какого-либо тела тем выше, чем больше отношение его поверхности к объему. В этом легко убедиться, если для тел различной формы сравнивать значения (на оси симметрии внутри тела) при одинаковых значениях Fo. Такое сопоставление приведено на рис. 4.15, где для различных тел даны зависимости при Bi →∞ . Здесь штрихом обозначена начальная температура поверхности тела.

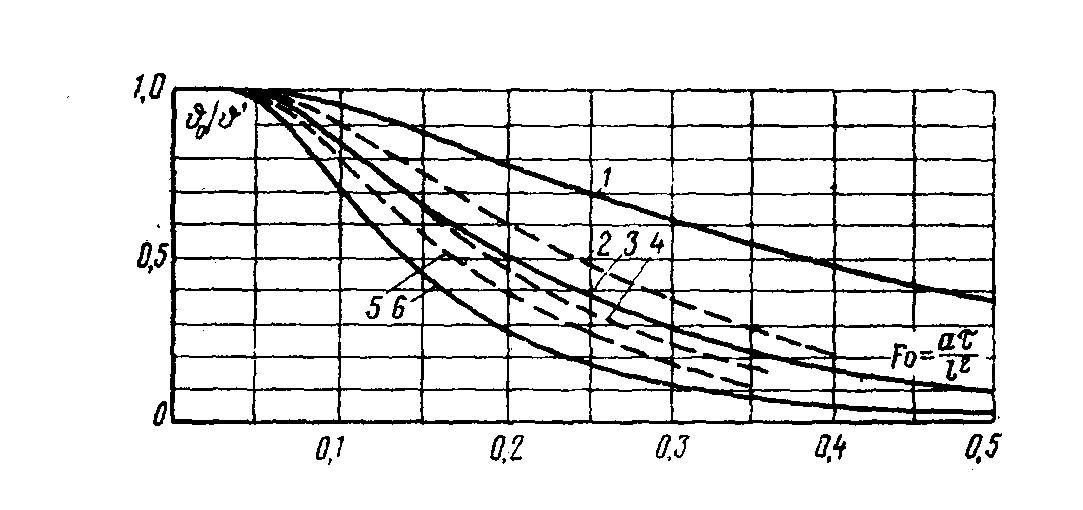
Рис.4.15. Зависимость температуры в центре для тел различной формы

1- пластина; 2 – квадратная балка бесконечной длины; 3- цилиндр бесконечной длины;

4 - куб; 5- цилиндр, длина равна диаметру; 6 – шар.

Из рисунка видно, что для шарообразных тел скорость процесса больше, чем для любых других. Для цилиндрических и призматических тел скорость процесса в сильной степени зависит от их длины. Чем меньше длина, тем выше скорость.

При построении графика использован метод суперпозиции. Короткие цилиндры, прямоугольные призмы и параллелепипеды можно рассматривать соответственно как тела, образованные пересечением взаимно перпендикулярных цилиндра и пластины, двух и трех пластин неограниченных размеров, но конечной толщины. Для цилиндра конечной длины толщина пластины 2δ берется равной длине цилиндра ℓ. Относительная температура

для какой-либо точки цилиндра равна произведению относительных температур этой точки, полученых для бесконечно длинного цилинра и пластины бесконечной протяженности. Для прямоугольных призм и параллелепипедов также применяется этот способ. Например, относительная температура на поверхности середины длины цилиндра равна произведению относительной температуры поверхности бесконечно длинного цилиндра на относительную температуру в середине неограниченной плиты ; точно так же относительная температура на оси в середине цилиндра равна произведению бесконечного цилиндра и неограниченной длины.

Опыт аналитических решений (функции Грина, метод тепловых потенциалов, интегральных преобразований и др.) изложен в специальной литературе. См. например [2,3,6,8]