
Lectures part1
.pdf- 81 -
одну из этих формул, то такая величина является тензором соответствующего ранга.
Сточки зрения тензорного подхода вектор является тензором первого ранга.
Всовременной механике деформируемых тел, как и в других отраслях науки и техники, широко используются понятие и свойства тензора. С его по- мощью можно записывать соотношения для произвольных систем координат, что, в частности, позволяет создавать универсальные программы для вычисли- тельных машин. Понятие тензора полезно ещё и тем, что позволяет предста-
вить себе напряженное состояние вблизи точки как одну многокомпонентную величину, не зависящую от выбора системы координат.
- 82 -
Тема №8. Деформированное состояние в точке трехмерного тела. Обобщенный закон Гука. Система уравнений теории
упругости и пути ее решения
Деформированное состояние в точке трехмерного тела
Деформированное состояние тела можно характеризовать перемещения- ми точек. Действительно, если имеется закрепленное до деформации тело, то при деформации все его точки переместятся в новое положение. Напомним,
что перемещением точки называется вектор U , проведенный из положения материальной точки тела до деформации А в ее положение А* после дефор-
мации (рис. 8.1), а составляющие вектора U по осям x, y, z обозначены в дан- ном курсе u, v, w.
Р |
Отметим, что перемещения то- |
|
чек могут использоваться и для неза- |
||
|
||
А |
крепленных тел. Но в этом случае они |
|
А* |
характеризуют не только деформации |
|
|
тела, но и его перемещение в про- |
|
Рис. 8.1 |
странстве. |
|
При рассмотрении растяжения |
стержня убедились, что неудобно пользоваться только абсолютными величи- нами перемещений. Кроме них вводилась относительная величина – относи- тельное удлинение, называемое еще линейной деформацией. Именно эта вели- чина связана законом Гука с нормальным напряжением. Другое напряжение, касательное, связано было законом Гука для сдвига с угловой деформацией.
В общем, трехмерном случае для характеристики деформированного со- стояния вблизи точки используются линейные деформации εx , ε y , εz и угло-
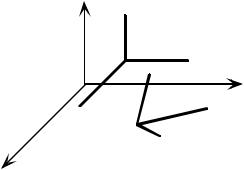
вые деформации γ xy , γ yz , γ zx . Рассмотрим в теле до деформации точки A, B, C, D (рис. 4.1), образующие отрезки AB = dx , AC = dy , AD = dz . Положение этих точек после деформации помечено на рис. 8.2 соответствующей буквой со звез- дочкой. Линейные деформации в точке А во всех координатных направлениях вводятся также, как в направлении координаты x при растяжении стержня
εx = |
A*B* − AB |
|
= |
(dx)* − dx |
|
, |
|
|
AB |
dx |
|
||||||
|
|
|
|
|||||
εy = |
A*C* − AC |
= |
(dy)* − dy |
, |
(8.1) |
|||
AC |
dy |
|||||||
|
|
|
|
|||||
|
|
|
- 83 - |
|
ez = |
A*D* - AD |
= |
(dz)* - dz |
. |
AD |
|
|||
|
|
dz |
||
Угловой деформацией назван угол, на который изменяется прямой угол в деформируемом твёрдом теле. Изменяться могут, очевидно, углы на всех плос- костях, проходящих через данную точку. Угловые деформации в плоскостях, параллельных координатным, вводятся соотношениями
g xy = ÐBAC - ÐB* A*C* = 90°-ÐB* A*C* , |
|
|||||
g yz = ÐCAD - ÐC* A*D* = 90°-ÐC* A*D* , |
(8.2) |
|||||
g zx = ÐDAB - ÐD* A*B* = 90°-ÐD* A*B* . |
углов равенства γ xy = γ yx , |
|||||
z |
|
|
|
|
Для |
|
D |
dz dy |
|
γ yz = γ zy , |
γ zx = γ xz очевидны и в доказа- |
||
|
A |
C |
тельстве не нуждаются в отличие от ка- |
|||
0 |
|
|
D* |
y |
сательных напряжений. Предельный пе- |
|
|
dx |
|
|
|
реход при записи формул (8.1–8.2) осу- |
|
B |
|
|
C* |
ществляется за счёт выбора отрезков |
||
A* |
B* |
|||||
x |
|
|
|
dx , dy , dz бесконечно малой длины. |
||
Рис. 8.2 |
|
|
Около данной точки для различных сис- |
|||
|
|
|
тем координат можно указать бесконеч- |
|||
|
|
|
|
|
но много линейных и угловых деформа- |
|
ций. Кроме того, деформированное состояние закреплённого тела можно также характеризовать перемещениями его точек. Различные величины, характери- зующие деформации вблизи точки, называют параметрами деформированного состояния в точке твердого тела, а само это физическое явление – деформи- рованным состоянием в точке.
Как и в случае напряжений, деформаций в данной системе координат шесть, и можно показать, что для них выполняется основной тензорный при- знак (7.38) и они также образуют симметричный тензор второго ранга (для это- го вводят коэффициент 0,5 при угловых деформациях).
Поэтому для деформаций, как и для напряжений, существуют главные оси и главные значения деформаций:
εmax = ε1 , ε2 , εmin = ε3 , |
(8.3) |
обладают они и всеми другими свойствами симметричных тензоров второго ранга.

- 84 -
Зависимости между деформациями и перемещениями
1.Зависимости между линейными деформациями и перемещениями
Идеформации, и перемещения закрепленного тела характеризуют одно и то же деформированное состояние тела, поэтому между этими двумя группами величин должны существовать зависимости. Получим их.
z 
A
α0 a
a
α
β B b A*
b A* a*
a*
β
x

Рис. 8.2
точек концов отрезков AB и
|
Изобразим снова точки A и B |
||
|
нижней грани бесконечно малого пря- |
||
C y |
моугольного параллелепипеда (рис. 8.2) |
||
до деформации и после деформации A* , |
|||
C* |
B* . Деформацию εx найдем исходя из |
||
B* |
ее определения: |
|
|
|
εx (x) = (dx)* − dx = |
A*B* − AB |
. (8.4) |
|
|
||
|
dx |
AB |
|
b* |
Для этого следует найти длины отрез- |
|
|
|
ков, входящих в формулу (8.4), что |
|
можно сделать с помощью координат |
A*B* (табл. 8.1). |
|
|
Таблица 8.1 |
Координаты точек
|
до деформации |
после деформации |
||
A |
|
B |
A* |
B* |
x |
|
x + dx |
x + u |
x + dx + uB |
y |
|
y |
y + v |
y + vB |
z |
|
z |
z + w |
z + wB |
Для записи координат точек A* , B* (после деформации) использованы перемещения точки А: u, v, w, и перемещения точки В: uB , vB , wB .
Точки А и В бесконечно близки друг к другу, поскольку расстояние меж- ду ними dx . В непрерывной задаче функции, заданные в этих точках, будут также бесконечно близкими, что можно выразить с помощью терминов мате- матики, с помощью дифференциалов. Однако в данном случае это будут част- ные дифференциалы по координате x:
uB |
= u + ∂xu = u + |
|
∂u |
dx , |
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
∂x |
|
||||
vB |
= v + ∂xv = v + |
∂v |
dx , |
(8.5) |
||||||
|
|
|||||||||
|
|
|
|
∂x |
|
|||||
w = w + ∂ |
x |
w = w + |
∂w |
dx . |
|
|||||
|
|
|||||||||
B |
|
|
|
|
∂x |
|
||||
|
|
|
|
|
|
|
||||
- 85 -
Конечно, AB = dx . Длина отрезка A*B* по координатам записывается по формуле аналитической геометрии:
A*B* = |
|
. |
|
(xB* - xA* )2 + (yB* - yA* )2 + (zB* - zA* )2 |
(8.6) |
однако она содержит радикал. Преобразуем формулу (8.4):
ex = |
A*B* |
- 1, |
|
|
(8.7) |
||||
AB |
|
|
|
|
|||||
|
A* B* |
|
|
||||||
откуда 1+ e x |
= |
|
|
||||||
|
|
|
|
. Возведя в квадрат, получим: |
|
||||
|
|
dx |
|
|
|||||
|
|
|
|
|
(A*B* )2 |
|
|
||
1 + 2ex |
|
2 |
= |
. |
(8.8) |
||||
+ ex |
(dx)2 |
||||||||
|
|
|
|
|
|
|
|
||
Теперь радикал для записи линейной деформации не потребуется.
Подставим в (8.6) значения координат точек A* и B* из табл. 8.1 с учётом
соотношений (8.5) и найдём квадрат длины отрезка A*B* |
|
||||||||
2 |
éæ |
¶u |
ö2 |
æ ¶v |
ö2 |
æ ¶w |
ö2 |
ù |
(8.9) |
(A*B* ) |
= êçdx + |
¶x |
dx÷ |
+ ç |
dx÷ |
+ ç |
dx÷ |
ú . |
|
|
êè |
ø |
è ¶x |
ø |
è ¶x |
ø |
ú |
|
|
|
ë |
|
|
|
|
|
|
û |
|
Полученный результат подставим в (8.8), раскроем скобки и сократим на (dx)2 :
1+ 2ex + e2x |
=1+ 2 |
¶u |
æ |
¶u ö2 |
¶x |
+ ç ÷ |
|||
|
|
è |
¶x ø |
|
+æ ¶v ö2 + æ ¶w ö2 ç ÷ ç ÷ , è ¶x ø è ¶x ø
откуда |
|
|
|
¶u ö2 |
|
¶v ö2 |
|
¶w ö2 |
|
2ex + e2x |
= 2 |
¶u |
æ |
æ |
æ |
(8.10) |
|||
¶x |
+ ç |
÷ |
+ ç |
÷ |
+ ç |
÷ . |
|||
|
|
è |
¶x ø |
è |
¶x ø |
è |
¶x ø |
|
При малых перемещениях и деформациях следует пренебречь нелинейными
2 |
æ |
¶u ö2 |
æ |
¶v ö2 |
|
слагаемыми ex |
, ç |
÷ |
, ç |
÷ |
, |
|
è |
¶x ø |
è |
¶x ø |
|
æ ¶w ö2
ç ÷ по сравнению с другими слагаемыми, т.е.
è ¶x ø
линеаризировать это соотношение: |
|
||||||||
ex = |
∂u |
. |
|
|
|
|
|
|
(8.11) |
|
|
|
|
|
|
|
|||
|
¶x |
|
|
|
|
|
|
|
|
Ещё два соотношения можно получить либо аналогично первому, либо |
|||||||||
исходя из равноправия направлений осей координат |
|
||||||||
ex = |
∂u |
, |
e y = |
∂v |
, |
e z = |
∂w |
. |
(8.12) |
|
|
|
|||||||
|
¶x |
|
¶y |
|
¶z |
деформации εx |
|||
Запишем |
далее некоторую величину, аналогичную |
||||||||
из (8.7): |
|
|
|
|
|
|
|
||
|
a*b* |
|
- 86 - |
|
~ |
|
|
||
ex = |
|
- 1 , |
(8.13) |
|
ab |
||||
|
|
|
но вместо отрезка AB пользуемся его проекцией на ось х – отрезком a*b* . Ко- ординаты крайних точек этого отрезка определим по рис. 8.2 (табл. 8.2).
|
|
|
|
|
A* |
|
|
B* |
|
|
|
|
|
|
x + u |
|
x + dx + uB |
|
|
|
|
|
|
0 |
|
0 |
|
||
|
|
|
|
0 |
|
0 |
|
||
Длина отрезка |
a*b* с учетом (8.5) |
запишется так: |
|
||||||
a*b* = x + dx + u + |
∂u |
∂u |
|
||||||
|
dx - x - u = dx + |
|
dx , |
(8.14) |
|||||
¶x |
¶x |
||||||||
поэтому |
∂u |
|
|
|
|
|
|
|
|
~ |
= ex . |
|
|
|
|
|
(8.15) |
||
ex = |
¶x |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Отсюда следует, что введенные упрощения соответствуют пренебрежению по- воротом отрезка AB = dx в процессе деформации.
|
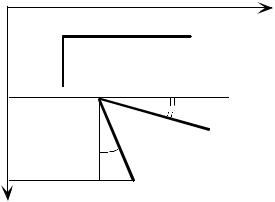
2. Угловые деформациями и перемещения. |
|
|
|
|
|
|
||||||
|
Далее исходя из определения |
|
|
|
|
|
|
|
|
||||
|
g xy = ÐBAC - ÐB* A*C* = 90°-ÐB* A*C* , |
|
|
|
|
|
|
(8.16) |
|||||
0 |
|
|
|
|
y |
запишем угловые деформации через пе- |
|||||||
|
a |
|
|
c |
|
ремещения. Угловые деформации будут |
|||||||
a |
|
|
|
найдены из отношений отрезков, до де- |
|||||||||
|
|
|
|
|
|||||||||
b |
b |
|
|
|
|
формации параллельных осям. Следует |
|||||||
a* |
|
|
|
снова пренебрегать поворотом отрезков, |
|||||||||
a |
p |
|
|
j |
2 |
чтобы получать угловые деформации с |
|||||||
|
|
|
|
|
той же степенью точности, как и линей- |
||||||||
|
|
|
|
|
c* |
||||||||
|
|
|
|
|
ные. Тогда вместо угла после деформа- |
||||||||
b |
|
j |
1 |
|
|
||||||||
|
|
|
ции ÐB |
* |
A |
* |
C |
* |
(рис. 8.2) |
можно рас- |
|||
x |
n |
m |
b* |
|
|
|
|
|
|||||
|
|
сматривать |
|
Ðb*a*c* , его |
проекцию на |
||||||||
|
Рис. 8.3 |
|
|
|
|||||||||
|
|
|
|
плоскость xOy . Для угла ÐBAC это |
|||||||||
|
|
|
|
|
|
||||||||
очевидно, поэтому изобразим плоскость xOy (рис. 8.3) и запишем |
|
||||||||||||
|
g xy » Ðbac - Ðb*a*c* = 90°-Ðb*a*c* = j1 + j2 . |
|
|
|
|
(8.17) |
|||||||
|
Найдем углы ϕ1 |
и ϕ2 , образующие угол γ xy , для малых перемещений и |
|||||||||||
деформаций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b*m |
|
b*n - nm |
|
|
- 87 - |
|||||
tgj » j = |
= |
= |
vB - vA |
, |
||||||||||
|
|
|
|
|
||||||||||
|
1 1 |
|
ma* |
a*b* |
|
|
a*b* |
|||||||
где vB и vA – |
перемещения точек A и В в направлении оси у. |
|||||||||||||
ношениями (8.5), где vA = v , (8.12) и (8.14), найдем |
||||||||||||||
|
|
|
∂v |
|
|
|
|
|
|
|
|
|||
j1 |
= |
vA + |
¶x dx - vA |
= |
¶v 1 |
|
. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
æ |
+ |
¶uö |
¶x 1+ e |
|
|
|||||||||
|
|
|
x |
|||||||||||
|
|
ç1 |
÷dx |
|
|
|
|
|
||||||
|
|
è |
|
¶xø |
|
|
|
|
|
|
|
|
||
(8.18)
Пользуясь соот-
(8.19)
Но для малых деформаций можно пренебречь линейной деформацией εx по сравнению с единицей:
1 + εx ≈1, |
|
|
|
|
|
|
|
|
|
|
|
(8.20) |
|||||||||
поэтому |
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
j1 |
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
(8.21) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
¶x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Нетрудно видеть, что аналогично запишется |
|
||||||||||||||||||||
j2 = |
|
∂u |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
¶y |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда согласно (8.17) |
|
|
|
|
|
|
|
|
|
||||||||||||
g xy = |
∂v |
+ |
∂u |
. |
|
|
|
|
|
|
|
|
|
(8.22) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
¶x |
¶y |
|
|
|
|
|
|
|
|
|
||||||
Формулы для γ yz и γ zx |
получаются аналогично или же просто циклической |
||||||||||||||||||||
перестановкой символов. |
|
|
|
|
|
|
|||||||||||||||
Таким образом, перемещения и деформации связаны в линейных задачах |
|||||||||||||||||||||
следующими шестью соотношениями: |
|
||||||||||||||||||||
ex |
= |
|
∂u |
|
, g xy = |
∂v |
|
+ |
∂u |
|
, |
|
|||||||||
|
¶x |
¶x |
¶y |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ey |
= |
|
∂v |
|
, |
g yz = |
|
∂w |
+ |
|
∂v |
|
, |
(8.23) |
|||||||
|
¶y |
|
¶y |
|
¶z |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ez |
= |
∂w |
, g zx = |
∂u |
|
+ |
∂w |
, |
|
||||||||||||
|
¶z |
¶z |
|
¶x |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
которые называются соотношениями Коши. Эти соотношения называют также деформационными, или кинематическим.
Обобщенный закон Гука. Физические соотношения.
Снова рассмотрим бесконечно малый параллелепипед со сторонами dx1, dx2 , dx3 . Предположим, что он находится в одноосном напряженном со-
стоянии в направлении оси x1 (т.е. растянут в этом направлении). Тогда в на-
- 88 -
правлении других главных осей напряженного состояния x2 и x3 он уменьшит свои размеры. Деформацию в направлении этих осей можно записать по закону Гука для растяжения-сжатия
ε* = σ1 |
, ε* |
= −με* = −μ σ1 |
, ε* |
= −με* = −μ σ1 . |
(8.24) |
|||
1 |
E |
2 |
1 |
E |
3 |
1 |
E |
|
|
|
|
|
|
|
|||
Напомним, что при этом σ2 = 0 и σ3 = 0 , поскольку деформация в поперечном направлении происходит без напряжений.
Предположим теперь, |
что напряжение σ2 |
действует только в направле- |
||||||||||||||||
нии оси х2. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ε1** = −μ |
σ2 |
, ε**2 = |
|
σ2 |
|
|
, ε**3 = −μ |
σ2 |
. |
|
(8.25) |
|||||||
|
|
E |
|
|
||||||||||||||
|
|
E |
|
|
|
|
|
|
E |
|
||||||||
Аналогично для напряжения σ3 : |
|
|
|
|
|
|||||||||||||
ε1*** = −μ |
σ3 |
|
, ε***2 |
= −μ |
σ3 |
, ε***3 |
= |
σ3 |
. |
(8.26) |
||||||||
E |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
E |
|
E |
|
||||||
При одновременном действии всех трех напряжений, по принципу су- |
||||||||||||||||||
перпозиции, одноименные деформации нужно складывать: |
||||||||||||||||||
ε1 = ε1* + ε1** + ε1*** = |
1 |
|
|
[σ1 − μ(σ2 |
+ σ3 )], |
|
||||||||||||
E |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ε2 = ε*2 + ε**2 |
+ ε***2 |
= |
1 |
|
[σ2 − μ(σ2 + σ1 )], |
(8.27) |
||||||||||||
E |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ε3 = ε*3 + ε**3 |
+ ε***3 |
= |
1 |
|
[σ3 − μ(σ1 + σ2 )]. |
|
||||||||||||
E |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Полученные соотношения уже представляют собой обобщенный закон Гука, записанный, однако, для главных осей напряжений и деформаций, по-
скольку на координатных площадках отсутствуют касательные напряжения и угловые деформации. Далее следует воспользоваться формулами, которые по-
зволяют выразить компоненты деформаций и напряжений на произвольных площадках через их главные значения и направляющие косинусы углов для произвольных площадок относительно главных. Эти формулы являются част- ным случаем формул (7.37). Поскольку законы изменения напряжений и де- формаций по углам поворота осей координат одинаковы, то для произвольных осей снова будут справедливы те же соотношения:
εx = E1 [σx
εy = E1 [σ y
εz = E1 [σz
− μ(σ y + σz )], |
|
− μ(σz + σx )], |
(8.28) |
− μ(σx + σ y )]. |
|
- 89 -
По главным значениям деформаций и напряжений вычисляются также значения угловых деформаций и касательных напряжений для произвольных площадок, что приводит к соотношениям
γ xy |
= |
|
τ xy |
, |
|
γ yz = |
τ yz |
, γ zx = |
τ |
zx |
, |
(8.29) |
|
|
G |
|
G |
|
|
||||||||
где |
|
|
|
|
|
|
|
G |
|
||||
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
G = |
|
|
|
|
|
. |
|
|
|
|
|
(8.30) |
|
|
2 1+ μ |
) |
|
|
|
|
|
||||||
|
|
|
( |
|
|
|
|
|
|
|
|
||
Соотношения (8.28) и (8.29) представляют собой обобщенный закон Гука для произвольных осей координат. Коэффициент G – модуль сдвига, для кото- рого заодно для общего случая получается соотношение (8.30), связывающее его с модулем на растяжение-сжатие и коэффициентом Пуассона.
Соотношения обобщенного закона Гука могут быть переписаны для вы- числения напряжений по деформациям. В сдвиговых уравнениях (8.29) это де-
лается элементарно |
|
τxy = Gγ xy , τyz = Gγ yz , τzx = Gγ zx . |
(8.31) |
В соотношениях (8.28) добавим и вычтем слагаемые с коэффициентом Пуассона, сумма нормальных напряжений даст независящую от выбора коор-
динат величину (первый инвариант напряжений), которую обозначим так |
|
|||||||||||
σ* = σx + σy + σz ; |
|
|
|
|
|
|
(8.32) |
|||||
εx = |
1 |
|
[σx + μσx − μσx − μ(σy + σz )]= |
1 |
|
[(1+ μ)σx − μσ* ]; |
|
|||||
E |
E |
|
||||||||||
|
|
|
[σy + μσy − μσy − μ(σz + σx )]= |
|
[(1+ μ)σy − μσ* ]; |
|
||||||
εy = |
1 |
|
1 |
|
(8.33) |
|||||||
E |
|
|
E |
|
||||||||
εz = |
|
1 |
|
[σz + μσz − μσz − μ(σx +σy )]= |
1 |
[(1+ μ)σz − μσ* ]. |
|
|||||
|
E |
|
|
|
||||||||
|
|
|
|
E |
|
|
|
|||||
Обозначим первый инвариант деформаций аналогично первому инварианту напряжений:
ε* = εx + ε y + εz |
(8.34) |
Сложив формулы (8.33), найдем зависимость между инвариантами:
ε* = 1− 2μ σ*. (8.35)
E
Теперь формулы (8.33) легко обращаются. Например, первая из них при-
нимает вид
|
μE |
E |
|
|
|
σx = |
|
ε* + |
|
εx = λε* + 2Gεx , |
(8.36) |
(1+ μ)(1− 2μ) |
1+ μ |
||||
что приводит к искомым равенствам обобщенного закона Гука во второй форме: σx = λε* + 2Gεx , τxy = Gγxy ,
σ y = λε* + 2Gε y , |
|
- 90 - |
|
||
|
τyz = Gγ yz , |
(8.37) |
|||
σz = λε* + 2Gεz , |
|
τzx = Gγzx , |
|
||
где введён новый коэффициент, характеризующий свойства материалов |
|
||||
λ = |
μE |
, |
|
(8.38) |
|
(1 + μ)(1 − 2μ) |
|
|
|||
а G – модуль сдвига.
Напомним, что закон Гука является частным видом физических соотно- шений, связывающих напряжения и деформации. Он справедлив при малых перемещениях и деформациях.
Система уравнений теории упругости.
Выпишем дифференциальные уравнения равновесия бесконечно малого элемента трехмерного упругого тела (6.14), соотношения обобщенного закона Гука (8.28) и (8.29) и соотношения Коши:
|
∂σ |
x |
+ |
|
∂τyx |
+ |
|
∂τ |
zx |
|
+ ρx |
= 0, |
|
|||||||||||||||||||
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
||||||||||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|||||||||||||
|
∂σy |
+ |
∂τzy |
|
+ |
|
∂τxy |
|
|
+ ρy |
= 0 , |
(8.39) |
||||||||||||||||||||
|
∂y |
|
|
∂z |
|
|
∂x |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
∂σ |
z |
|
+ |
∂τ |
xz |
|
|
+ |
∂τyz |
|
+ ρz |
= 0 . |
|
||||||||||||||||||
|
∂z |
|
|
|
∂x |
|
|
∂y |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
σx = λε* + 2Gεx , τxy = Gγxy , |
|
|||||||||||||||||||||||||||||||
σ y |
= λε* + 2Gε y , |
|
τyz = Gγ yz , |
(8.40) |
||||||||||||||||||||||||||||
σz = λε* + 2Gεz , |
|
|
|
|
τzx = Gγzx , |
|
||||||||||||||||||||||||||
ε |
x |
= |
|
∂u |
|
, γ |
xy |
= |
|
|
∂v |
|
|
+ |
|
∂u |
|
, |
|
|
||||||||||||
|
∂x |
|
|
|
∂x |
|
|
|
∂y |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ε |
y |
= |
|
∂v |
, γ |
yz |
= |
|
|
∂w |
+ |
|
∂v |
|
, |
|
(8.41) |
|||||||||||||||
|
∂y |
|
|
∂y |
|
∂z |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
εz = |
|
∂w |
, γzx = |
|
|
∂u |
|
+ |
|
∂w |
, |
|
|
|||||||||||||||||||
|
|
|
|
∂z |
|
∂x |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
В уравнения (8.39) – (8.41) входят 15 |
неизвестных функций координат |
|||||||||||||||||||||||||||||||
точки упругого тела: три компонента перемещения (u,v,w ), шесть компонентов деформаций (εx ,εy ,εz ,γxy , γ yz ,γzx ) и шесть компонентов напряжений (σx , σy , σz , τxy , τyz , τzx ). Объемные силы ρx , ρy , ρz , характеристики материала λ, G ,
а также геометрия конструкции считаются известными.
Уравнений тоже 15, однако большая часть из них дифференциальные в частных производных. Дифференциальные уравнения требуют для однознач-
