
Lectures part1
.pdf- 91 -
ного решения задания граничных условий. Такими условиями в данном случае будут условия на границе, краю тела. На части границы, где заданы опорные связи рассматриваемого тела, граничными (краевыми) условиями будет равен-
~r
ство вектора перемещений U точек тела перемещениям опорных связей U
r r |
|
~ |
(8.42) |
U = U |
|
Если же опоры абсолютно твердые, то перемещения опор нулевые. Тогда |
|
на границе |
|
U = 0 |
(8.43) |
~r
На другой части границы могут быть задан вектор внешнего давления s , он должны быть равен в точках границы напряжению σ (внутреннему давле- нию), поэтому на другой части контура граничное условие будет иметь вид:
r |
|
~ |
(8.44) |
s = s , |
|
для свободного же края без нагрузки условием на границе будет |
|
σ = 0. |
(8.45) |
Переписанные в проекциях на оси координат граничные (точнее краевые) условия (8.42), (8.44) или их варианты записи (8.43), (8.45) должны быть при- соединены к системе уравнений (8.39) – (8.41), после чего она становится замк- нутой. Это система уравнений в частных производных высокой сложности, по- скольку она содержит 15 неизвестных функций трех координат, например σx = σx (x, y, z), γ zx = γ zx (x, y, z), u = u(x, y, z) и т.д. В общем случае ее решение можно осуществить только численными методами, хотя в частных случаях возможно и аналитическое ее решение.
Для решения эти уравнения обычно преобразуют, уменьшая число урав- нений и основных неизвестных. Используют два основных пути решения этой системы уравнений: решение в напряжениях или же решение в перемещениях. В первом случае из системы уравнений исключаются деформации и перемеще- ния. Решение получающейся системы уравнений относительно напряжений оказывается несколько более сложной, чем при решении в перемещениях, и используется реже. Более употребительным является второй путь.
Уравнения для решения краевой задачи теории упругости в перемещениях.
В качестве основных неизвестных, подлежащих определению в первую очередь, принимаются три функции компонентов вектора перемещений:
u = u(x, y, z),v = v(x, y, z),w = w(x, y, z) . |
(8.46) |
Подстановка в равенства обобщенного закона Гука, записанного в фор- ме (8.40), соотношений Коши даёт соотношения для напряжений, входящих в
первое из уравнений равновесия (8.39), |
|
|
|
|
|
|
|
|||||||||
s |
|
= le* + 2G |
¶u |
, t |
|
æ |
¶v |
+ |
¶u |
ö |
|
æ |
¶u |
+ |
¶w ö |
(8.47) |
x |
|
yx |
= Gç |
|
|
÷, t |
zx |
= Gç |
|
÷, |
||||||
|
|
¶x |
|
ç |
¶x |
|
¶y |
÷ |
è |
¶z |
|
¶x ø |
|
|||
|
|
|
|
|
è |
|
ø |
|
|
|
||||||
где |
|
|
|
|
|
|
- 92 - |
|
∂u |
|
∂v |
|
∂w |
|
|
||
e* = |
+ |
+ |
. |
(8.48) |
||||
¶x |
¶y |
|
||||||
|
|
|
¶z |
|
||||
Подстановка выражений (8.47) для напряжений в уравнение равновесия после
группировки членов приводит к уравнению
|
¶e* |
|
¶ æ |
¶u |
|
¶v |
|
¶w ö |
æ |
¶2u |
|
¶2u |
|
¶2u ö |
|
|
|
|
|||||
l |
|
+ G |
|
ç |
|
+ |
|
+ |
÷ |
+ Gç |
|
2 |
+ |
|
2 |
+ |
|
2 |
÷ |
+ g |
x |
= 0. |
(8.49) |
|
|
|
|
|
|
|
|||||||||||||||||
|
¶x |
|
ç |
¶x |
|
¶y |
|
÷ |
ç |
¶x |
|
¶y |
|
¶z |
÷ |
|
|
|
|||||
|
|
¶x è |
|
|
¶z ø |
è |
|
|
|
|
|
ø |
|
|
|
|
|||||||
Используя (8.48), и учтя, что выражение во вторых круглых скобках есть опе-
ратор Лапласа
( ) |
|
¶2 |
L |
|
¶2 L |
|
¶2 L |
|
|
|
|
|
( ) |
|
( ) |
|
( ) |
|
|
||
D L |
= |
|
+ |
+ |
, |
(8.50) |
||||
¶x2 |
¶y2 |
¶z2 |
||||||||
|
|
|
|
|
|
|||||
получим первое, а по аналогии и остальные уравнения равновесия в перемещениях
(l + G) |
¶ æ |
¶u |
+ |
¶v |
+ |
¶wö |
+ GDu + rx = |
|||
|
ç |
|
¶y |
¶z |
÷ |
|||||
|
|
|||||||||
|
|
¶x è ¶x |
|
|
ø |
|
||||
|
|
¶ |
æ |
¶u |
|
¶v |
|
|
ö |
|
(l + G) |
|
ç |
+ |
+ |
¶w÷ |
+ GDv + ry = |
||||
|
|
|
¶y |
|||||||
|
|
¶y è ¶x |
|
|
¶z ø |
|
||||
(l + G) |
¶ |
æ |
¶u |
+ |
¶v |
+ |
¶wö |
+ GDw + rz = |
||
|
ç |
|
¶y |
¶z |
÷ |
|||||
|
|
|||||||||
|
|
¶z è ¶x |
|
|
ø |
|
||||
0,
0 , |
(8.51) |
0.
Таким образом, мы пришли к системе трех дифференциальных уравне- ний в частных производных относительно трех неизвестных функций переме- щений точек тела u(x, y, z),v(x, y, z),w(x, y, z). Система получается значительно
более обозримой, чем исходная. Легче видеть и граничные условия, необходи- мые для решения системы. Действительно, каждое из уравнений имеет второй порядок. Для их решения необходимо по два граничных условия для каждой переменной. Такие условия в начале и в конце интервала, т.е. граничные (крае- вые) условия, очевидно всегда можно указать.
Граничные условия для перемещений (8.42) или (8.43) сохранят свой вид, условия же для напряжений (8.44) или (8.45) необходимо переписать, исполь- зуя равенства, подобные (8.47). Уравнения (8.51) называются уравнениями Ла- ме. Если их удается решить аналитически или численно, то по найденным функциям перемещений с помощью соотношений Коши (8.41) определяются сначала деформации, а затем из обобщенного закона Гука (8.40) вычисляются напряжения.

- 93 -
Тема №9. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ
СЕЧЕНИЙ
В формулы сопротивления материалов входят величины, представляю- щие собой интегралы по площади поперечных сечений. Значения этих инте- гралов зависят только от геометрии этих сечений. Прежде чем изучать изгиб и кручение стержней, рассмотрим вспомогательный вопрос – свойства и способы вычисления этих интегралов.
Статические моменты плоского сечения
Статическими моментами плоского сечения называются интегралы вида
Sy = òzdF , |
Sz = ò ydF . |
(9.1) |
F |
F |
|
Это – чисто геометрические интегралы. Поясним, почему они называются мо- ментами.
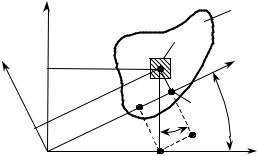
Рассмотрим пластину постоянной толщины h из материала с удельным весом ρ , который действует в направлении оси x (рис. 9.1). Выделим малый элемент объема Vi , как показано на рисунке. Поскольку площадь этого эле- мента на лицевой поверхности пластины Fi , то объем этого элемента
Vi = h Fi , вес Pi = ρh Fi , а момент относительно оси y : M yi = ρhzi Fi .
|
z |
|
Fi |
h |
|
Vi |
||
|
||
|
zi |
0 |
y |
|
h |
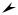 x
x
Рис. 9.1
Суммируя моменты всех подоб- ных элементов пластины, получим на-
стоящий статический момент сил веса этой пластины относительно оси y :
i=∞ |
i=∞ |
M y = åρhzi |
Fi = ρh åzi Fi . |
i=1 |
i=1 |
Бесконечная сумма в этом выражении является интегральной, поэтому
M y = ρhòzdF ,
F
откуда видно, что данный момент отличается от статического момента площа- ди сечения только постоянным множителем (отсюда название «статический момент» площади сечения).
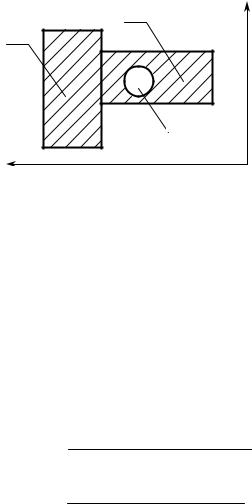
По тем же соображениям используется понятие центра тяжести сечения.
Центр тяжести – это точка, в которой приложена равнодействующая сил веса. Статический момент системы сил (в том числе сил веса) относительно оси, проходящей через точку приложения их равнодействующей, равен нулю.
|
|
|
- 94 - |
|
|
|
Поскольку момент равнодействующей равен сумме моментов состав- |
||||||
ляющих, то, если yc , zc – координаты центра тяжести в некоторых произволь- |
||||||
ных осях, для силы веса ρhF можем записать |
|
|
|
|||
|
i=∞ |
|
|
|
|
|
ρhFzc = åρhzi Fi = M y . |
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
Заменим бесконечную сумму интегралом и сократим на ρh : |
|
|||||
Fzc |
= òzdF , |
|
|
|
|
|
|
F |
|
|
|
|
|
поэтому |
= S y , Fyc = Sz . |
|
|
|
|
|
Fzc |
|
|
|
|
(9.2) |
|
где yc , zc |
– координаты центра тяжести сечения (а не только пластины). |
|||||
|
|
|
|
Координатные оси, |
проходящие |
|
|
II |
y |
через |
центр |
тяжести, |
называются |
I |
центральными. |
|
|
|||
|
|
|
|
|||
|
|
|
Так как |
определенный интеграл |
||
|
|
|
|
|||
|
|
|
представляет собой бесконечную сум- |
|||
|
|
|
му, то статический момент обладает |
|||
|
III |
|
свойством аддитивности по области. |
|||
|
|
|
Тогда |
статический момент составного |
||
z |
|
0 |
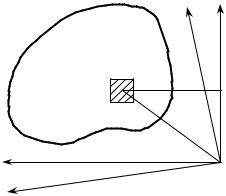
сечения (рис. 9.2) относительно некото- |
|||
|
рой оси y можно представить как сум- |
|||||
|
Рис. 9.2 |
|
||||
|
|
му статических моментов элементов, |
||||
|
|
|
составляющих |
сечение. |
Отверстие |
|
в этом случае можно рассматривать как элемент с отрицательным статическим |
||||||
моментом и площадью поперечного сечения, поэтому |
|
|
||||
S y = SI y + SII y − SIII y , |
|
|
|
|
(9.3) |
|
откуда, учитывая (9.3): |
|
|
|
|
|
|
zc (FI + FII − FIII )= zIcFI + zIIcFII − zIIIcFIII . |
|
|
||||
В итоге получаются формулы для определения центра тяжести сечения, со- |
||||||
стоящего из элементов с известным положением центра тяжести: |
|
|||||
yc = yIc FI + yIIc FII − yIIIc FIII |
; |
|
|
|
|
|
|
FI + FII − FIII |
|
|
|
|
(9.4) |
zc = zIc FI + zIIc FII − zIIIc FIII . |
|
|
|
|||
|
|
|
|
|||
|
FI + FII − FIII |
|
|
|
|
|
|
- 95 - |
|
Моменты инерции плоских сечений и их простейшие свойства |
||
Интегралы по площади сечения |
|
|
I y = òz2dF, |
Iz = ò y2dF |
(9.5) |
F |
F |
|
I yz = ò yzdF , |
|
(9.6) |
F |
|
|
I p = òr2dF . |
|
(9.7) |
F |
|
|
называются моментами инерции плоского сечения, причём |
I y , Iz – осевые |
|
моменты инерции, I yz – центробежный момент инерции, I p – полярный мо-
мент инерции.
Как и статические моменты, эти величины совпадают с точностью до множителя ρh с инерционными характеристиками пластины, изображенной на
рис. 9.1 (см. курс теоретической механики). |
|
||
Нетрудно видеть: |
|
|
|
I p = I y + Iz , |
|
|
(9.8) |
действительно, из рис. 9.3 получаем |
|
||
I y + Iz = òz2dF + ò y2dF = ò(z2 + y2 )dF = òr2dF = I p . |
|||
F |
F |
F |
F |
Но I p это определенный интеграл, некоторое постоянное для данного сечения число. Поскольку для любых осей, например ξ и η (рис. 9.3), поверну- тых на произвольный угол относительно начала координат, справедливо равен-
ство
r2 = y2 + z2 = ξ2 + η2 . |
|
|
Тогда |
|
|
I p = I y |
+ Iz = Iξ + Iη = const . |
|
|
ξ |
y |
|
|
|
|
dF |
|
|
z |
|
|
r |
y |
z |
|
0 |
ξ |
|
|
|
Рис. 9.3 |
|
(9.9)
Таким образом, нами получено свойство осевых моментов инерции:
Сумма осевых моментов инерции не меняется при повороте осей коорди- нат.
Кроме того, из определений мо- ментов инерции очевидно, что осевые и центробежный моменты инерции вели- чины всегда положительные.
Так как момент инерции, как и ста-
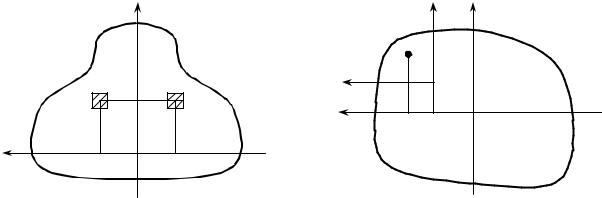
|
|
|
|
- 96 - |
|
|
тический момент, есть интеграл, то он также обладает свойством аддитивности, |
||||||
как и статический момент, так что для одной и той же оси y момент инерции |
||||||
сечения на рис. 9.2 можно представить в виде суммы: |
|
|||||
Iy = I yI + I yII |
− IyIII . |
|
|
(9.10) |
||
Здесь для отверстия снова используется тот же прием. Момент инерции отвер- |
||||||
стия взят со знаком минус. |
|
|
|
|||
Центробежный же момент инерции может быть как положительным, так |
||||||
и отрицательным. Центробежный момент инерции для осей, одна из которых |
||||||
является осью симметрии сечения, равен нулю. Докажем это свойство. |
||||||
Ось y сечения на рис. 9.4 является осью симметрии. Представим центро- |
||||||
бежный момент всего сечения как сумму центробежных моментов, вычислен- |
||||||
ных по его левой и правой частям (относительно этой оси): |
|
|||||
I yz = ò yzdF = ò yл zлdFл + ò yп zпdFп . |
|
(9.11) |
||||
F |
|
Fл |
|
Fп |
|
|
Для любого элемента dFл существует равный ему элемент dFп . Очевид- |
||||||
ны следующие равенства |
|
|
|
|||
yл = yп , zл = −zп , Fл = Fп . |
|
|
||||
Тогда |
|
|
|
|
|
|
I yz = ò yл zлdFл + ò yп zпdFп = − ò yп zпdFп + ò yп zпdFп = 0, |
||||||
Fл |
|
|
Fп |
Fп |
Fп |
|
что и требовалось доказать. |
|
|
|
|||
|
|
y |
|
|
y |
yc |
|
|
|
|
|
A |
|
|
zл zп |
|
|
0 |
|
|
dFл y |
dFп |
z |
y0 |
ц.т. |
||
л |
y |
zc |
z0 |
0c |
||
|
п |
|
|
|
||
z |
|
0 |
|
|
|
|
Рис. 9.4 |
|
Рис. 9.5 |
||||
Докажем некоторые другие свойства моментов инерции, которые пона- |
||||||
добятся нам в дальнейшем. |
|
|
|
|||
Моменты инерции сечения относительно осей, параллельных центральным
Найдем момент инерции относительно оси y (рис. 9.5), исходя из его оп- ределения. Если yс, zс – координаты точки А в центральных осях, y0 , z0 – коор-
|
|
|
|
|
|
|
|
- 97 - |
|
динаты точки 0 в центральных осях (расстояний между осями), то координаты |
|||||||||
точки А в произвольных осях, как видно из рисунка, записываются так: |
|||||||||
|
y = yc − y0 , z = zc − z0 . |
|
|
(9.12) |
|||||
Тогда в определении момента инерции можно сделать замену переменной и |
|||||||||
представить интеграл в виде суммы интегралов по отдельным слагаемым |
|||||||||
|
I y = òz2dF = ò(zc − z0 )2 dF = òzc2dF − 2z0 òzcdF + z02 òdF . |
||||||||
|
|
|
F |
F |
|
F |
F |
F |
|
Поскольку z0 – константа для данной пары осей, то она вынесена из-под знака |
|||||||||
интеграла, кроме того |
|
|
|
|
|||||
|
I yc = òzc2dF, S yc =òzcdF = 0, F = òdF , |
|
|||||||
|
|
|
|
F |
|
F |
|
F |
|
поэтому |
= I |
|
+ z2F , |
|
|
|
|
||
|
I |
y |
yc |
|
|
|
(9.13) |
||
|
|
|
0 |
|
|
|
|
||
аналогично можно получить ещё две формулы |
|
||||||||
|
I |
z |
= I |
zc |
+ y2F |
|
|
|
|
|
|
|
0 |
|
|
|
(9.14) |
||
|
Iyz = Iyc zc + yzF |
|
|
|
|||||
|
|
|
|
|
|||||
|
Таким образом, формулами (9.13), (9.14) можно воспользоваться, если |
||||||||
известны моменты инерции относительно центральных осей, а требуется опре- |
|||||||||
делить моменты инерции относительно произвольных осей, параллельных цен- |
|||||||||
|
|
z |
|
|
|
|
F |
тральным. Если обратить эти форму- |
|
|
|
|
|
|
dF |
лы, то можно и по известным для про- |
|||
|
|
|
|
|
a |
|
извольных осей |
моментам инерции, |
|
η |
|
z |
|
|
e |
ξ |
определить их для центральных осей. |
||
|
|
|
|
||||||
|
|
|
|
|
d |
|
Но необходимо, |
чтобы одна из пар |
|
|
|
|
|
|
ξ |
α |
|||
|
|
|
|
|
была бы парой центральных осей. Для |
||||
|
η |
|
|
|
α |
|
|||
|
|
|
b |
c |
|
произвольных пар параллельных осей |
|||
|
|
0 |
|
y |
y |
формулы записываются сложнее. Эти |
|||
|
|
|
|
||||||
|
|
|
|
|
Рис. 9.6 |
|
|
формулы часто называют формулами |
|
|
|
|
|
|
|
|
Штернера. |
|
|
|
|
|
Изменение моментов инерции при повороте осей координат. |
||||||
Если известны моменты инерции относительно некоторой пары осей ко- ординат x и y, то несложно вычислить моменты инерции относительно любых других осей, например ξ и η, повернутых на некоторый угол α относительно
исходных осей (рис. 9.6). Для этого надо записать по определению моменты инерции в новых осях, а затем сделать замену переменной с помощью формул,
- 98 -
выражающих зависимости между координатами одной и той же точки в разных парах осей. Эти формулы можно получить непосредственно из рисунка
ξ = 0d + de = y cosα + zsin α ,
(9.15)
h = ac - ce = -ysin a + z cosa ,
или взять из справочника по математике. Тогда первый из осевых моментов инерции запишется так:
Iξ = òh2dF = ò(- ysin a + z cosa)2 dF =
|
|
F |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
æ |
|
2 |
ö |
|
2 |
|
æ |
|
2 |
ö |
2 |
æ |
|
ö |
= |
ç |
ò y |
÷ |
|
a + |
ç |
òz |
÷ |
ç |
|
÷ |
||||
ç |
|
dF ÷sin |
|
ç |
|
dF ÷cos |
|
a - 2ç |
ò yzdF ÷sin acosa = |
||||||
|
è F |
|
ø |
|
|
|
è F |
|
ø |
|
è F |
ø |
|||
= Iξ = I y cos2 a + Iz sin2 a - I yz sin 2a . |
(9.16) |
||
Аналогично получаются ещё две формулы |
|
||
Iη = I y sin2 a + Iz cos2 a + I yz sin 2a , |
(9.17) |
||
Iξη = |
I y - Iz |
sin 2a + I yz cos2a , |
|
2 |
|
||
|
|
|
|
Формулы (9.16), 9.17 очень напоминают формулы (7.7), (7.8), (7.10) для напряжений при плоском напряженном состоянии. Они полностью совпадут, если поменять знак у всех касательных напряжений (или центробежных мо- ментов) на противоположный. Можно показать, что шесть массовых моментов инерции твердого тела Ix , I y , Iz , Ixy , I yz , Izx образуют подобно напряжениям
симметричный тензор второго ранга, доказав для них формулы (7.37). Мы же обнаружили подобие формул в частном, плоском случае. Очевидно, что свой- ства таких величин должны совпадать. В данном случае они совпадают с точ- ностью до непринципиального отличия в знаках. Поэтому нет необходимости снова выводить тем же путём те же самые формулы и свойства.
Так, среди всех пар осей, проходящих через данную точку сечения, обычно существуют главные оси и главные моменты инерции. Центробежный момент инерции для главных осей равен нулю, а осевые моменты инерции принимают в этих осях максимальное и минимальное значения. Направления главных осей от-
носительно заданных определяются углом αгл :
tg 2aгл = |
2I yz |
. |
(9.18) |
||
Iz |
- I y |
||||
|
|
|
|||
Заметим, что формула записана для правой системы координат. Данная форму- ла в левой системе координат отличается знаком.
Главные моменты инерции определяются проще всего по формулам
|
|
|
|
1 |
|
|
- 99 - |
|
|
|||||
|
|
|
|
é |
|
|
|
|
|
ù |
|
|||
|
|
|
|
|
2 |
|
2 |
|
||||||
|
Imax = I1 |
= |
|
|
êI y |
+ Iz + |
(I y - Iz ) |
+ |
4I yz ú |
, |
||||
2 |
||||||||||||||
|
|
|
|
ë |
|
|
|
|
û |
(9.19) |
||||
|
|
|
|
1 |
é |
|
|
|
|
|
ù |
|||
|
|
|
|
|
2 |
|
2 |
|
||||||
|
Imin = I2 |
= |
|
|
êI y |
+ Iz - |
(I y - Iz ) |
+ |
4I yz ú . |
|||||
2 |
||||||||||||||
|
|
|
|
ë |
|
|
|
|
û |
|
||||
|
Моменты инерции произвольных осей по их главным значениям вычис- |
|||||||||||||
ляются так |
|
|
|
|
|
|
|
|
|
|
|
|||
|
Iξ = I1 cos2 b + I2 sin2 b , |
|
|
|
|
|
|
|||||||
|
Iη = I1 sin2 b + I2 cos2 b , |
|
|
|
(9.20) |
|||||||||
|
Iξη = |
I1 - I2 |
sin 2b . |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
Из этих формул видно, что если равны |
|||||||
|
|
|
|
|
|
x1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
главные моменты инерции I1 = I2 , то |
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
i 1 |
|
|
|
i 2 |
|
|
|
равными будут и все прочие осевые |
|||||
|
|
|
|
|
|
|
|
моменты инерции для осей с тем же |
||||||
x2 |
|
|
|
|
|
|
|
началом координат Iξ = Iη = I y = Iz = I . |
||||||
Все эти оси и моменты инерции тоже будут главными.
Рис. 9.7 Главные оси с началом координат в центре тяжести сечения называются главными центральными осями сечения.
В теории расчета стержней используются эти оси, поэтому нужно уметь находить их положение и значения главных моментов инерции центральных осей.
Радиус инерции. Эллипс инерции Радиусами инерции называются величины:
iy = |
|
I y |
|
, iz = |
|
I |
z |
|
. |
(9.21) |
F |
|
|
|
|||||||
|
|
|
|
|
F |
|
||||
Измеряются эти величины, как видно из формул, в единицах длины. По глав- ным моментам инерции вычисляются главные радиусы инерции:
i1 = |
|
I1 |
|
, i 2 = |
|
I2 |
|
. |
(9.22) |
F |
|
||||||||
|
|
|
|
|
F |
|
|||
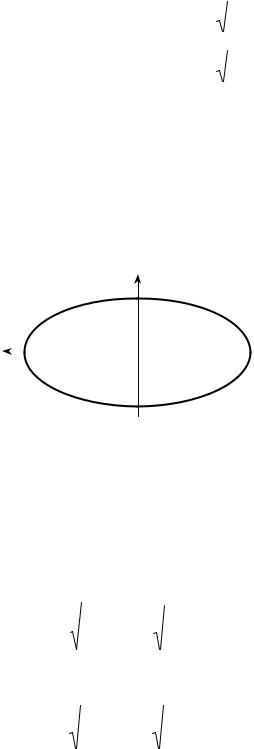
Эллипс, построенный на главных радиусах инерции как на полуосях, на-
зывается эллипсом инерции. При этом радиус инерции принято откладывать перпендикулярно своей оси (рис. 9.7), поэтому уравнение эллипса для главных
осей x1, x2 имеет вид |
|
|||||
|
x2 |
|
x2 |
|
|
|
|
1 |
+ |
2 |
=1 . |
(9.23) |
|
i 22 |
i 12 |
|||||
|
|
|
|
|||
- 100 -
Эллипс инерции использовался для графического определения моментов инерции относительно осей, что не актуально при наличии вычислительной техники. Но он объясняет название «радиусы инерции», а радиусы инерции ис- пользуются в технической литературе.
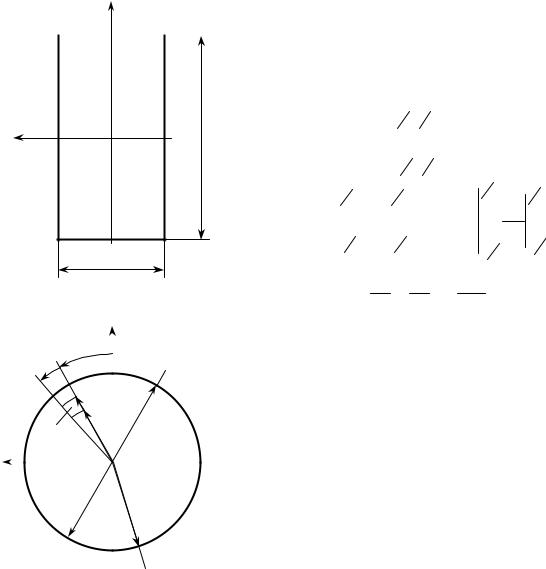
Моменты инерции простейших сечений
y |
Формулы для моментов инерции сечений |
|
простых очертаний могут быть получены анали- |
|
тически. Рассмотрим прямоугольное сечение |
|
(рис. 9.8). Учитывая независимость интегрирова- |
|
ния по координатам y и z, запишем |
|
|
|
|
|
|
|
b |
|
|
h |
|
|
|
|
|
|
|
|
||
z |
h |
Iz = ò y2dF = ò2 |
|
|
ò2 y2dydz = |
|
|
|
||||||||||||
|
|
F |
|
|
|
|
−b |
2 |
−h |
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
æ b 2 |
öæ b 2 |
|
|
2 |
|
|
ö |
|
b 2 |
|
y |
3 h 2 |
||||||
|
|
ç |
|
֍ |
|
ò y |
|
|
÷ |
= z |
|
|
= |
|||||||
|
|
= ç |
òdz ÷ç |
|
|
|
dy÷ |
|
3 |
|||||||||||
|
b |
è |
−b 2 |
øè |
−b 2 |
|
|
|
|
|
|
ø |
|
−b |
2 |
−h 2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
3 |
|
|
|
h |
3 |
ö |
|
bh |
3 |
|
|
|
|
||
|
|
|
ç h |
|
|
+ |
|
|
|
÷ |
= |
|
. |
|
|
(9.24) |
||||
|
|
|
= b |
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
||||
|
Рис. 9.8 |
|
ç |
24 |
|
|
24 |
|
12 |
|
|
|
|
|||||||
|
|
è |
|
|
ø |
|
|
|
|
|
||||||||||
|
dϕ |
ϕ |
|
|
y |
|
|
|
D |
|
|
Аналогично |
3 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Iy = hb . |
|
|
|
|
(9.25) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку оси y и z являются осями симметрии |
||||||||||||||
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
dF |
|
|
|
|
|
|
|
|
|
|
|
прямоугольника, тогда I yz |
= 0 . |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получим |
моменты |
инерции |
для круглого |
||||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
сечения (рис. 9.9). Начнем с определения поляр- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ного момента инерции. В полярной системе ко- |
|||||||||||||
|
|
|
|
|
|
|
|
|
R |
|
|
ординат заменим интегралы по площади на инте- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
гралы по координатам |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
Рис. 9.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π R |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I p = òr2dF = ò |
òr2rdrdj = |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
F |
|
|
|
|
0 |
0 |
|
|
|
|
|
|
2π öæ R |
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
æ |
2 |
ö |
|
|
r4 |
|
R4 |
|
|
|
pR4 |
pD4 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
ç |
|
֍ |
òr |
÷ |
= j |
|
|
|
|
|
== 2p |
|
|
|
= |
|
= |
|
. |
(9.26) |
|||||
|
|
= ç |
òdj÷ç |
|
|
rdr ÷ |
4 |
|
|
|
4 |
|
|
2 |
32 |
||||||||||||
|
|
è |
0 |
øè |
0 |
|
|
ø |
|
|
|
0 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Но поскольку I p = I y + Iz , а I y |
= Iz для круга, то осевой момент инерции |
||||||||||||||||||||||||||
