
Lectures part1
.pdf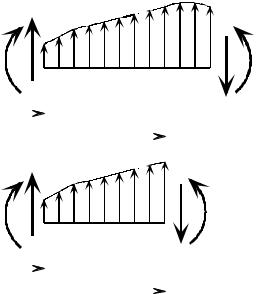
x |
- 31 - |
|
|
M (x) = Mн + òQdx , |
(3.24) |
xн
что, однако, не совпадает с формулой (3.20). Поставим формулу (3.23) в (3.24), тогда
x æ x |
ö |
|
ç |
÷ |
(3.25) |
M (x) = M н + Qн (x - xн ) + ò ç òqdx |
÷dx . |
|
xн è xн |
ø |
|
Может показаться, что формулы (3.20) и (3.25) различаются, но в курсе математике показывается, что интеграл, входящий в формулу (3.25) и называе- мый повторным интегралом, может вычисляться, в частности, по алгоритму соответствующего слагаемого в формуле (3.20):
x æ x |
ö |
|
ç |
÷ |
(3.26) |
ò ç òqdx |
÷dx = FAXCD (x - xц.т. ) . |
|
xн è xн |
ø |
|
Mн |
Qн |
|
|
|
|
|
Если закон распределения q по длине |
||||
|
|
|
|
|
достаточно сложный или эта функция зада- |
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
на таблично, то пользоваться формулой |
|||
|
|
A |
|
|
B |
|
|
(3.20) неудобно, поскольку |
для |
каждого |
|
|
|
|
|
|
|
||||||
xн |
|
|
|
M |
|
значения x необходимо находить центр тя- |
|||||
|
|
|
|
Qк |
к |
||||||
|
|
|
|
|
|
жести сложной фигуры. В этом случае для |
|||||
|
|
|
x |
|
|
|
|||||
|
|
|
|
|
|
|
определения значений эпюр Q(x) и M(x) |
||||
|
|
|
|
|
|
|
|||||
|
Qн |
|
|
C |
|
|
|||||
Mн |
|
|
|
|
пользуются |
последовательно |
формулами |
||||
|
D |
|
|
|
|
|
(3.23) и (3.24). Именно так поступают, на- |
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
пример, при построении эпюр от аэродина- |
|||
xн |
|
A |
X |
|
M(x) |
|
|
мической нагрузки крыла самолета. |
|
||
|
|
|
|
|
|||||||
|
|
|
|
Q(x) |
|
|
Заметим, кроме того, что алгоритм по- |
||||
|
|
|
|
|
|
|
|||||
|
|
|
x |
|
|
|
|
строения эпюр эквивалентен операции ин- |
|||
|
|
|
|
|
|
|
|||||
|
|
|
Рис. 3.4 |
|
|
|
|
тегрирования |
дифференциальных |
уравне- |
|
|
|
|
|
|
|
|
ний равновесия. Этого и следовало ожидать, |
||||
|
|
|
|
|
|
|
|
||||
поскольку при построении эпюр используются те же уравнения равновесия, но в интегральной форме.
|
|
|
|
- 32 - |
|
|
РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ |
||
|
Тема №4. Напряжения, деформации и перемещения при растяжении |
|||
|
|
невесомого стержня. Закон Гука |
||
|
Основные результаты эксперимента на растяжение стержня при малых |
|||
|
перемещениях и деформациях |
|||
|
|
|
|
При построении эпюр изучались инте- |
|
A |
A |
|
гральные силовые факторы, передающиеся в |
|
|
целом через поперечное сечение абсолютно |
||
|
|
|
|
|
|
|
|
|
жесткого тела. Названная тема очевидно бли- |
1 |
x |
|
|
же по содержанию к теоретической механике. |
l |
|
|
||
1 |
|
|
|
Перейдем теперь к изучению усилий в каждой |
l |
|
|
|
точке конструкции, т.е. собственно к сопро- |
1 |
|
|
|
|
|
|
|
|
|
l |
|
|
|
тивлению материалов (механике деформируе- |
|
l |
|
к |
|
|
|
l |
мого твердого тела). Знание усилий в каждой |
|
b |
|
bк |
|
|
|
|
точке позволяет судить о прочности конст- |
||
|
|
|
|
|
|
B |
|
|
рукции. |
|
|
|
В основе всякого знания, всякой науки |
|
|
l |
B* |
|
|
|
|
|
лежит опыт, эксперимент. Эксперимент, свя- |
|
|
|
P |
|
занный с растяжением стержней, лежит в ос- |
|
|
|
нове сопротивления материалов и теории уп- |
|
|
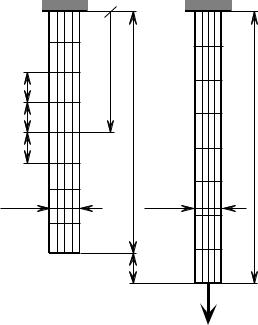
Рис. 4.1 |
|
||
|
|
ругости. |
||
|
|
|
|
|
|
Не описывая реальный эксперимент, приведем только его краткое описа- |
|||
ние и обобщенные результаты. Отметим, что проводимые в ходе лабораторных |
||||
работ эксперименты на растяжение, хотя и похожи на описываемый экспери- |
||||
мент, но имеют другие цели и не могут дать все отмеченные ниже результаты. |
||||
|
Допустим, что для испытаний взят прямой однородный изотропный ме- |
|||
таллический стержень с прямоугольным поперечным сечением (рис. 4.1). Дли- |
||||
на стержня много больше его поперечных размеров. Один конец стержня за- |
||||
крепляется на абсолютно жесткой опоре. На поверхности стержня наносится |
||||
прямоугольная сетка линий. Продольные линии параллельны оси стержня. За- |
||||
тем стержень подвергается действию растягивающей силы P, приложенной к |
||||
его концу строго вдоль оси стержня. Под действием этой силы стержень удли- |
||||
няется, но пусть сила будет такая, что это удлинение не превышает долей про- |
||||
цента от первоначальной длины стержня. Весом же стержня пренебрегаем, по- |
||||
лагая, что сила Р много больше веса стержня. |
||||
|
По сетке линий можно судить о характере распределения деформаций в |
|||
- 33 -
стержне. Линии сетки остаются прямыми и перпендикулярными друг к другу. Размеры всех ячеек сетки изменяются одинаково. Продольные размеры ячеек увеличиваются, поперечные уменьшаются. Отклонения могут наблюдаться только в зоне приложения активной силы и опорной реакции.
A
x
l
X
B
|
|
|
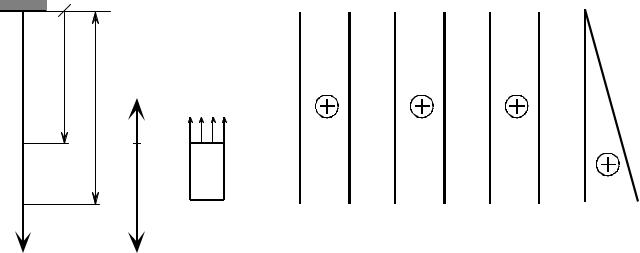
Эпюры: N (x) |
|
σ (x) |
|
ε (x) |
|
|
u(x) |
|
|
|
|||||||||||
|
N (x) |
|
|
A |
|
A |
|
A |
|
A |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
B |
B |
|
B |
|
B |
|
B |
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 4.2
На основе этой картины деформирования была сформулирована гипоте-
за плоских сечений: материальные точки стержня, до деформации находив- шиеся в одной плоскости поперечного сечения стержня, после деформации осевого растяжения-сжатия остаются в одной плоскости и эта плоскость остаётся перпендикулярной продольной оси стержня.
Подобные гипотезы относительно характера распределения перемещений точек при деформации называются кинематическими.
Меняя значение силы Р, площадь поперечного сечения стержня, длину, а также материал, из которого изготовлен стержень, можно убедиться, что при
малых нагрузках и стандартной температуре справедлива зависимость |
|
||
l = k |
Pl |
, |
(4.1) |
|
F |
|
|
где k – коэффициент, меняющий значение при смене материала стержня, т.е. он является механической характеристикой материала стержня. Однако использу- ется не она, а величина, ей обратная. Соотношение (4.1) представляет собой один из вариантов записи закона Гука, о котором, как и о некоторых других результатах эксперимента, скажем ниже в данной теме.
Уравнения равновесия и напряженное состояние невесомого стержня
Часть результатов эксперимента можно было предсказать. Действитель- но, мы можем построить эпюру осевой силы N(x) в стержне (рис. 4.2), пользу- ясь методом сечений. Уравнение равновесия отсеченной нижней части стержня
|
|
|
|
|
- 34 - |
|
|
|
|
|
ХВ в направлении продольной оси дает постоянную внутреннюю силу, равную |
||||||||||
внешней нагрузке: |
|
|
|
|
|
|
|
|
|
|
|
N(x) = P. |
|
|
|
|
|
|
|
|
|
|
Но тогда любой участок стержня растянут одними и теми же силами |
|||||||||
N (x) = P , и неудивительно, что все равные по длине отрезки стержня дефор- |
||||||||||
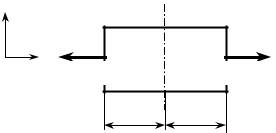
мируются одинаково. Участок стержня произвольной длины от сечения D − D |
||||||||||
до сечения E − E симметричен и нагружен симметрично (рис. 4.3). Плоскость |
||||||||||
поперечного сечения C − C является плоскостью симметрии. В этих условиях |
||||||||||
точки сечения не могут выйти при деформации из плоскости, в результате се- |
||||||||||
чение должно остаться плоским после деформации и нормальным к продоль- |
||||||||||
ной оси стержня. Поскольку такое рассуждение справедливо для произвольно- |
||||||||||
го сечения, то все сечения должны оставаться плоскими. Симметрия, однако, |
||||||||||
может нарушаться при неравномерном распределении сил |
N (x) по попереч- |
|||||||||
ному сечению. Так и происходит у концов стержня, где закон распределения |
||||||||||
сил по крайнему сечению может отличаться от распределения сил по внутрен- |
||||||||||
ним сечениям стержня (удаленным от его концов). |
|
|
|
|
||||||
|
|
|
|
|
Чтобы обосновать утверждение |
о |
||||
y |
D |
C |
|
E |
том, что |
поперечное |
сечение |
|
остается |
|
|
плоским |
необходимо |
принять |
принцип |
||||||
|
|
|
|
|
||||||
|
|
|
|
|
Сен-Венана. Считаем |
стержень |
весьма |
|||
0 x |
N (x) = P |
|
N (x) = P длинным, как и его участок на рис. 4.3. |
|||||||
|
D a |
C |
a |
E |
Согласно принципу Сен-Венана, внутрен- |
|||||
|
ние усилия в центральной части участка |
|||||||||
|
|
|
|
|
не зависят от законов распределения уси- |
|||||
|
Рис. 4.3 |
|
|
|
лий по сечениям D − D и E − E . Главные |
|||||
|
|
|
|
же векторы сил в сечениях |
D − D |
и |
||||
E − E симметричны относительно сечения. Если предположить, что в условиях |
||||||||||
симметрии задачи принцип Сен-Венана можно распространить и на деформи- |
||||||||||
рованное состояние, то центральное сечение должно остаться плоским в сим- |
||||||||||
метричной задаче, а поскольку оно произвольно, то плоским останутся и все |
||||||||||
другие сечения в средней части стержня. Приведенные рассуждения доказа- |
||||||||||
тельством назвать нельзя, они лишь являются обоснованием гипотезы о том, |
||||||||||
что сечения остаются плоскими. Эта гипотеза принимается, в конечном счете, |
||||||||||
на основе эксперимента. |
|
|
|
|
|
|
|
|
||
|
Если сечения остаются плоскими, то все продольные элементы деформи- |
|||||||||
руются одинаково, что свидетельствует о равномерности распределения силы |
||||||||||
N по поперечному сечению. |
|
|
|
|
|
|
|
|||
|
Рассмотрения сил N, однако, недостаточно для решения вопроса о проч- |
|||||||||

- 35 -
ности. Ведь при одной и той же силе N, допустим в 100 кгс, материал колонны здания будет недогружен, а оси механизма часов – перегружен. Ясно, что о на- груженности материала, а следовательно, и о прочности следует судить по от- носительной величине, т.е. по силе, приходящейся на единицу площади попе-
речного сечения стержня F: |
|
||||
σ |
ср |
= |
N |
= σ . |
(4.2) |
|
|
F |
|
|
|
Величина σ называется нормальным напряжением, нормальным – поскольку используется сила, действующая по нормали к сечению. По итогам экспери- мента сила N распределяется равномерно по сечению. Поэтому вычисляемое по формуле (4.2) среднее напряжение σср равно напряжению в каждой точке σ
поперечного сечения (рис. 4.2). Измеряется напряжение в системе СИ, очевид- но, в силах на единицу площади, т.е. в ньютонах на квадратный метр (паска- лях) ( Н м2 = Па ), как и давление. Да это и есть давление соседних слоев мате-
риала друг на друга, но в данной задаче это давление не совсем обычное, дав- ление на отрыв. Если рассмотреть задачу сжатия, то нормальное напряжение окажется обычным давлением соседних слоев материала друг на друга. Но Нм2 очень малая единица измерения и в практических расчетах обычно ис-
пользуют Н мм2 = МПа . В рассматриваемой задаче нормальное напряжение
оказывается постоянным во всех поперечных сечениях стержня. Только на концах стержня постоянство напряжений может нарушаться, однако учитывать эти отклонения в данном курсе не будем.
Таким образом, нормальным напряжением называется давление по нор- мали к рассматриваемому сечению внутри твердого тела.
Деформированное состояние невесомого стержня.
Рассмотрим подробнее деформированное состояние и его количествен- ные характеристики.
Р 
А
 А*
А*
Рис. 4.4
Введем понятие "перемещение" точек деформируемого тела.
Перемещением точки A закреп- ленного в пространстве деформируе-
|
мого твердого тела |
будем называть |
||||
|
r |
|
|
|
|
|
= AA* , проведенный из по- |
||||||
|
||||||
|
вектор U |
|||||
|
ложения точки A до деформации в ее |
|||||
|
положение |
|
после |
деформации A* |
||
- 36 -
(рис. 4.4).
Составляющие этого вектора по осям x, y, z обозначим соответственно u, v, w.
При испоьзовании гипотезы плоских сечений очевидно, что для описания деформации стержня в осевом направлении достаточно следить за перемеще- ниями точек продольной оси стержня u, чтобы получить осевые перемещения всех иных его точек.
В результате приложения нагрузки длина стержня изменится на некото-
рую величину |
|
l = lк − lн , |
(4.3) |
где lк – длина стержня после приложения нагрузки (конечная длина), lн - начальная длина стержня.
Величина l носит название абсолютного удлинения стержня и в дан-
ном случае равна перемещению точки B: l = uB . Очевидно, что при приложе- нии нагрузки перемещения получат и все другие точки оси стержня, и что они будут отличаться от перемещения точки B (рис. 4.1). Например, точка на опоре A совсем не будет перемещаться, uA = 0. Таким образом, перемещение будет функцией координаты x точки: u = u(x) .
Если мы имеем дело с колонной здания, и она от нагрузки изменила свою длину на 1 см, то материал колонны деформирован мало. Если на 1 см измени- ла свою длину ось механизма часов, то ее можно выкинуть. Чтобы получить характеристику деформированности материала, а не конкретного стержня, на-
до ввести в рассмотрение относительную величину
ε = |
l |
= |
l − l |
|
||
l |
к |
н |
. |
(4.4) |
||
l |
|
|||||
|
н |
|
н |
|
|
|
Эта величина называется относительным удлинением, или линейной деформа-
цией. Она представляет собой отношение приращения длины к первоначальной длине и является безразмерной. Заметим, что при малых деформациях в знаме- нателе формулы (4.4) можно использовать как lн, так и lк, разница в результа-
тах будет пренебрежимо малой.
Из (4.4) следует, что l = εlн , или в других обозначениях u(xB ) = εxB .
Поскольку любую часть стержня можно рассматривать как стержень меньшей длины, нагруженный той же силой N (x) = P , поэтому для любой точ- ки стержня перемещение есть u(x) = ~ε x . Однако не очевидно, что ~ε = ε . По-
кажем это.
На стержне нами были выделены участки равной длины (рис. 4.1). Обо- значим длину ячейки l1. Абсолютное удлинение одной ячейки обозначим соот- ветственно l1. Это удлинение одинаково для всех ячеек сетки, так как они
- 37 -
одинаковы и растянуты одинаковыми силами. Тогда и относительное удлине-
ние у всех участков одинаково: |
||
ε 1= |
l1 . |
|
|
l1 |
|
Если взять теперь участок стержня длиной, например, 3l1 , то его абсо- |
||
лютное удлинение будет равно 3 l 1, а относительное: |
||
ε3= |
3 l1 |
= ε1= ε = const . |
|
||
|
3l1 |
|
Поскольку аналогичным образом можно показать постоянство деформации для любого участка длины стержня, приходим к выводу о том, что величина ε в данной задаче есть величина постоянная, и тогда перемещения точек связаны с
относительным удлинением соотношением |
|
u (x) = εx , |
(4.5) |
где ε = const . Существование данной зависимости следовало ожидать, так как обе величины u и ε характеризуют одно и то же деформированное состояние.
Помимо деформации удлинения в продольном направлении происходят также деформации сжатия в поперечном направлении. Если bк – толщина стержня после деформации, b – толщина до деформации, то абсолютное сужение b есть
b = bк − b < 0 .
Относительное сужение, или линейная деформация в поперечном на-
правлении εп по аналогии с предыдущим безразмерная величина:
εп = |
b |
< 0 . |
(4.6) |
|
b |
||||
|
|
|
Другим важным результатом эксперимента, о котором еще не упомина- лось, является равенство, связывающее деформации в продольном и попереч- ном направлении:
εп = −με , |
(4.7) |
где μ безразмерная константа, определяемая экспериментально. Для разных
материалов она имеет разные значения в зависимости от их физических свойств и называется коэффициентом Пуассона. Аналитически может быть показано, что этот коэффициент может принимать значения 0 до 0,5, обычно 0,15-0,4, для сталей и дюраля ≈ 0,3.
Закон Гука для растяжения-сжатия. Физические соотношения
Деформации являются следствием внутренних сил и наоборот, внутрен- ние силы возникают, если тело деформировать, поэтому между величинами этих групп должны существовать определенные соотношения, учитывающие

- 38 -
физические свойства материалов. Эти зависимости называются физическими соотношениями. Для большинства материалов до определенного уровня на- грузки напряжения и деформации связаны прямо пропорциональной зависимо-
стью (рис. 4.5), которую записывают так |
|
σ = Eε . |
(4.8) |
Она получается из экспериментально устанавливаемого равенства (4.1), если
дополнительно обозначить
E = 1 . |
|
|
|
k |
|
|
|
Действительно, учтем, что P = N(x), и перепишем (4.1) в форме: |
|
||
N(x) = E |
l |
= E u(x) . |
(4.9) |
F |
l |
x |
|
Использовав теперь формулы для нормальных напряжений σ и линейных де- формаций ε (определения этих величин), приходим к равенству (4.8), которое
σ |
|
|
|
называется законом Гука. Закон Гука представляет |
|
|
|
собой частный случай физических соотношений. Ко- |
|
|
|
|
||
|
|
|
|
эффициент пропорциональности Е в этой формуле |
|
|
|
|
называется модулем упругости на растяжение или |
|
|
|
|
модулем упругости первого рода. Поскольку ε – ве- |
|
|
|
|
личина безразмерная, то из (4.8) следует, что модуль |
0 |
|
ε |
||
|
упругости измеряется в тех же единицах, что и на- |
|||
|
|
|
|
|
|
Рис. 4.5 |
|
|
пряжение. Если ε = 1, что соответствует увеличению |
|
|
|
длины растягиваемого стержня вдвое, то σ = E . Та- |
|
|
|
|
|
|
ким образом, модуль упругости – это нормальное напряжение, при котором длина растягиваемого стержня должна увеличиться вдвое (если бы закон Гука
продолжал действовать при таких уровнях деформаций и соответствующих им напряжений). Из сказанного следует, что модуль упругости имеет очень боль- шие значения, например для стали он ≈200000 Н мм 2 .
мм 2 .
Если в пределах действия закона Гука приложенную ранее нагрузку сбро- сить, то тело полностью восстановит свою первоначальную форму.
Свойство твердых тел полностью восстанавливать свою первоначаль- ную форму после снятия нагрузки называется упругостью.
Обозначим
с= EFl ,
иперепишем равенство (4.9):
N = |
EF |
l = с l , |
(4.10) |
|
l |
|
|
- 39 -
коэффициент с называется коэффициентом жесткости, при умножении на
него абсолютного удлинения получается величина приложенной к стержню растягивающей силы. Обратный ему коэффициент
α = 1 c |
(4.11) |
называется коэффициентом податливости, при умножении на него силы по-
лучается абсолютное удлинение: |
|
l = α N . |
(4.12) |
Очевидно, что растянутый стержень ведёт себя как пружина высокой жё- сткости и малой податливости. Произведение EF называется жесткостью се-
чения на растяжение.
При больших деформациях и напряжениях закон Гука нарушается и пе- реходит в более сложную физическую зависимость. Надо сказать, что закон Гука является приближенным. При очень малых деформациях он точен, а затем физическая зависимость всё больше отклоняется от прямой.
Замечания.
1.Напряжения и деформации связаны друг с другом, сопровождают друг друга. По- этому состояние тела под нагрузкой называют напряженно-деформированным состояни-
ем (НДС).
2.При рассмотрении задач в механике деформируемых тел выделяют три стороны во- проса, три группы соотношений:
а) теория напряженного состояния – это соотношения, связанные с уравнениями рав- новесия и содержащие напряжения;
б) теория деформированного состояния, или кинематические (геометрические) соот- ношения;
в) физические соотношения, связывающие первые две группы соотношений.
3.В пределах действия закона Гука при сжатии большинство материалов имеет те же свойства, что и при растяжении.
4.Напряженно-деформированное состояние материала стержня при растяжении нами рассмотрено еще не в полном объеме.
Касательные напряжения и угловые деформации для сечений, проведенных под произвольным углом к оси стержня.
Закон Гука для сдвига
Проведем сечение не под прямым углом к оси стержня (рис. 4.6). Зада- дим направление этого сечения углом α, который оно составляет с направлени- ем поперечного сечения. Как и раньше, отсеченная часть должна остаться в равновесии, поэтому осевая сила в стержне по-прежнему равна внешней на- грузке: N (x) = P . Но эта сила уже не будет нормальной к сечению. Разложим

- 40 -
её на две составляющие по аксиоме параллелограмма: Nα и Tα . Поскольку сила N (x) распределяется равномерно по сечению, силы Nα и Tα также распределятся равномерно по наклонному сечению площадью Fα , причем, как видно из рис. 4.6:
A
x
B
R = P
A
x
 α
α
Tα 
N ( x)= P
R = P
A
|
x |
α |
α |
|
τα |
Nα |
σα |
F = |
F |
; |
|
cosα |
|
||
α |
|
|
|
Nα = N (x) cosα ; |
(4.13) |
||
Tα = N (x) sin α |
|
||
Нормальное напряжение на на- клонной площадке снова, как и при по- лучении (4.2), вычислится как среднее
σα = Nα . (4.14)
Fα
Аналогично можно поступить и с силой Tα , лежащей в плоскости сечения
τα = |
Tα |
. |
(4.15) |
|
|||
|
Fα |
|
|
P |
Получается величина той же раз- |
|
мерности и природы, что и нормальное |
||
Рис. 4.6 |
||
напряжение, это тоже сила на единицу |
площади сечения, которая, благодаря равномерному распределению сил по се- чению, также вычисляется как среднее значение по сечению. Ее отличие от нормального напряжения в том, что сила расположена в плоскости сечения.
Величина τα называется касательным напряжением.
Подставляя значения Nα , Tα , Fα из (4.13) в (4.14) и (4.15), получим вы- ражения для нормального и касательного напряжений (σα , τα ) для произволь- но ориентированного сечения через значения нормальных напряжений σ в по-
перечном сечении и значение угла между сечениями
σα = |
|
N (x) |
cos2 |
α = σcos2 α |
(4.16) |
|||
|
|
|
||||||
|
|
F |
|
|
|
|
||
τα = |
N (x) |
sinα cosα = |
1 |
σsin2α |
(4.17) |
|||
|
2 |
|||||||
|
|
F |
|
|
|
|||
Заметим, что поскольку касательное напряжение направлено противоположно оси y, то его следует считать отрицательным. Однако вычисляется оно по положительным величи- нам, поэтому в формулах (4.15), (4.17) следует поставить знак минус, если требуется не только вычислить значение, но и указать направление касательного напряжения:
τα = − Tα , τα = − 1 σ sin 2α .
Fα 2
