
Lectures part1
.pdf
- 71 -
небрегать по сравнению с другими слагаемыми. Запишем уравнение равнове-
сия для оси η |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
åηi |
= τξηFξ + (σx sinα)Fx = 0, |
|
|
|
|
|
(7.3) |
||||||||||||
отсюда |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
τζη = −σx sinαcosα = − |
σx sin2α . |
|
|
|
|
(7.4) |
|||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
Посмотрим характерные значения напряжений для площадок различной |
||||||||||||||||||||
ориентации с помощью полученных формул: |
|
|
|
|
|||||||||||||||||
|
|
α = |
0°: |
σξ = σx , |
|
|
τξη = 0 . |
|
|
|
|
|
|
||||||||
|
|
α = 45° : σξ = 0,5σx , |
|
τξη |
|
= τmax = 0,5σx . |
|
|
|
(7.5) |
|||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
α = 90° : σξ = 0, |
|
|
τξη = 0 . |
|
|
|
|
|
|
||||||||||
|
|
Видим, что полученные нулевые значения σ и τ соответствуют нашему |
|||||||||||||||||||
определению одноосного напряженного состояния. |
Наибольшее нормальное |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
напряжение |
действует |
вдоль оси |
||
|
|
|
|
|
y |
|
σx |
|
|
|
|
|
|
|
|
одноосного |
напряженного |
состоя- |
|||
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
ния. Наибольшие касательные на- |
|||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
A |
|
|
|
τxy |
|
|
α |
|
|
|
η |
пряжения действуют под углом 45° |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
к оси одноосного напряженного со- |
||||||||
σy |
|
|
τyx |
|
|
|
|
|
|
|
C |
||||||||||
|
|
|
|
|
|
|
|
|
τξη |
|
стояния и равны половине наи- |
||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
больших |
нормальных. |
Вспомним, |
|||
|
|
|
|
|
|
|
σξ |
|
|
|
|
что «проскальзывание» слоев мате- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
риала при пластических деформаци- |
||||||||
|
|
|
B |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
α |
|
|
ξ |
|
|
|
|
ях происходит именно |
при |
углах, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рис. 7.5 |
близких к 45° . |
|
Эти результаты были получе- |
||
|
||
|
ны ранее при рассмотрении напря- |
жений на наклонных площадках при растяжении, хотя способ рассуждений в данном случае более общий. Очевидно, что одноосное напряженное состояние возникает при растяжении-сжатии стержней, но не только. Возникает оно и при чистом изгибе стержней. Возможно возникновение одноосного напряжен- ного состояния в отдельной точке или в локальной зоне материала. В соседних точках может быть уже более сложное напряженное состояние.
Плоское напряженное состояние.
Напряжения на наклонных площадках
Допустим, что вблизи некоторой точки А в твердом теле, находящемся в равновесии, в направлении плоскости x0y имеет место плоское напряженное

- 72 -
состояние. Определим напряжение на произвольной площадке, перпендику- лярной этой плоскости. Для этого снова мысленно вырежем из тела бесконечно малую прямую треугольную призму, две боковые грани которой перпендику- лярны осям x и y, а нормаль к третьей (напряжение на которой и будем опреде- лять) образует угол α с осью x (рис. 7.3). На рис. 7.5 показаны все напряжения, действующие в данном случае на призму. Из равновесия этой призмы следует, что сумма проекций всех сил на ось ξ должна быть равна нулю:
åξi = 0 = σξ Fξ − σ x cosαFξ cosα − σ y sinαFξ sinα − |
(7.6) |
|
− τxy sinαFξ cosα − τ yx cosαFξ sinα |
||
|
||
Откуда получим: |
|
|
σξ = σx cos2 α + σy sin2 α + τxy sin2α . |
(7.7) |
|
Тогда для площадки, перпендикулярной оси η (т.е. |
при αη = α + 90°), |
воспользовавшись соответствующими тригонометрическими формулами, бу- дем иметь:
ση = σx sin2 α + σy cos2 α − τxy sin2α |
(7.8) |
Сумма проекций всех сил на ось η дает |
|
|
åηi = τξηFξ + σx sin αFξ cosα − σ y cosαFξ sin α − |
(7.9) |
|
− τxy cosαFξ cosα + τyx sin αFξ sin α = 0, |
||
|
откуда с учетом парности касательных напряжений:
τξη = σy − σx sin2α + τxy cos2α . (7.10) 2
Таким образом, нами получены формулы (7.7), (7.8), (7.10) для определе- ния всех компонентов плоского напряженного состояния σξ , ση , τξη в других
произвольных осях. |
|
Вычислим сумму |
|
σξ + ση = σx (cos2 α + sin2 α)+ σy (sin2 α + cos2 α)= σx + σy , |
(7.11) |
откуда следует, что сумма нормальных напряжений на координатных площад-
ках при плоском напряженном состоянии не меняется при данном повороте координатных осей.
Подчеркнем также, что нами установлены законы изменения компонен- тов напряжений при повороте координатных осей относительно оси z вблизи одной и той же произвольной точки А. Так что достаточно знать компоненты напряжений хотя бы в одних осях, в любых других осях их легко пересчитать с помощью полученных формул.
- 73 -
Главные площадки при плоском напряженном состоянии
Главными площадками называются взаимно перпендикулярные площад- ки, на которых касательные напряжения равны нулю.
Из условия равенства нулю касательного напряжения на произвольной площадке с помощью соотношения (7.10) получаем уравнение
|
τξη = 0 = |
σ y |
− σx |
|
sin 2αгл + τxy cos2αгл , |
(7.12) |
||||
|
2 |
|
||||||||
откуда |
|
|
|
|
|
|
|
|||
2τxy |
|
|
|
|
|
|
||||
|
tg2αгл = |
|
|
. |
|
|
(7.13) |
|||
|
σx |
− σ y |
|
∂σξ |
|
|||||
|
|
|
|
|
|
|||||
Вычислим теперь производную |
из (7.7) |
и найдем углы α , при которых |
||||||||
∂α |
||||||||||
∂σξ |
|
|
|
|
|
|
|
|
||
= 0, а потому σ |
ξ |
|
принимают экстремальные значения. Получим именно |
|||||||
|
|
|||||||||
∂α |
|
|
|
|
|
|
|
|||
экстремумы, а не точки перегиба с нулевой производной, поскольку функции, входящие в выражения для σξ , не имеют точек перегиба:
|
∂σξ |
= 0 = −2σx cosαsinα + 2σy sinαcosα + 2τxy cos2α, |
(7.14) |
||
|
|
||||
|
∂α |
|
|
|
|
откуда |
|
|
|
||
|
(σ y − σx )sin2α + 2τxy cos2α = 0, |
(7.15) |
|||
|
tg2α = |
2τxy |
|
||
|
|
. |
(7.16) |
||
|
σx − σy |
||||
Формула (7.16) полностью совпала с (7.13), что говорит о том, что на
главных площадках помимо равенства нулю касательных напряжений есть и еще одна особенность. На этих площадках нормальные напряжения принимают максимальное и минимальное значения.
Анализируя значения угла, удовлетворяющие равенству (7.13), можно ви- деть, что существуют две главные площадки, повернутые относительно друг друга на угол 90°, что следует из свойств функции тангенса. На одной из них σξ = σmax , на другой ση = σmin .
Нормальные напряжения на главных площадках носят название главных напряжений.
Главные напряжения принято обозначать так: σmax = σ1, σmin = σ2 .
Примем оси, соответствующие главным площадкам, в качестве исходных при повороте осей. Положив касательные напряжения в формулах (7.7), (7.8),

- 74 - |
|
(7.10) равными нулю, придем к равенствам |
|
sξ = s1 cos2 a + s2 sin2 a, |
(7.17) |
sη = s1 sin2 a + s2 cos2 a, |
(7.18) |
tξη = σ2 − σ1 sin2a, |
(7.19) |
2 |
|
которые позволяют вычислить напряжения на площадках, произвольно ориен- тированных относительно главных.
Теперь несложно получить и формулы, по которым можно определить нор-
мальные напряжения на главных площадках по напряжениям на произвольных площадках. Для этого вычтем (7.18) из (7.17) и запишем результат в таком виде
sξ - sη = (s1 - s2 )cos2a . |
|
|
|
|
|
|
|
|
(7.20) |
||||||||
Перепишем и формулу для касательных напряжений (7.19): |
|
||||||||||||||||
2tξη = -(s1 - s2 )sin2a . |
|
|
|
|
|
|
|
|
|
|
(7.21) |
||||||
Теперь возведем в квадрат и сложим последние два равенства. С учетом |
|||||||||||||||||
основного тригонометрического тождества будем иметь |
|
||||||||||||||||
(sξ - sη )2 + 4tξη2 = (s1 - s2 )2 , |
|
|
|
|
|
|
|
(7.22) |
|||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s1 - s2 = |
|
(sξ - sη )2 + 4t2ξη |
. |
|
|
|
|
|
|
|
|
(7.23) |
|||||
С другой стороны, из предыдущего мы знаем, что |
|
||||||||||||||||
σ1 + σ2 = σξ + ση . |
|
|
|
|
|
|
|
|
|
|
|
(7.24) |
|||||
Складывая и вычитая последние два равенства, находим |
|
||||||||||||||||
|
|
|
|
1 |
é |
|
|
|
|
|
|
|
|
|
ù |
|
|
smax = s1 |
= |
|
+ |
(sξ |
- sη ) |
2 |
2 |
|
|
|
, |
(7.25) |
|||||
|
2 |
êsξ + sη |
|
+ 4tξη ú |
|||||||||||||
|
|
|
|
ë |
|
|
|
|
|
û |
|
|
|||||
|
|
|
|
1 |
é |
|
|
|
|
|
|
|
|
ù |
|
|
|
smin = s2 |
= |
|
- |
(sξ |
- sη ) |
2 |
2 |
|
|
|
(7.26) |
||||||
|
2 |
êsξ + sη |
|
+ 4tξη ú . |
|||||||||||||
|
|
|
|
ë |
|
|
|
|
|
û |
|
|
|||||
Вместо греческих букв в полученных равенствах можно писать соответ- |
|||||||||||||||||
ствующие латинские |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
é |
|
|
|
|
|
|
|
ù |
|
|
||
|
|
|
|
|
(sx |
- s y ) |
2 |
2 |
|
|
|
||||||
smax = s1 |
= |
|
|
êsx + s y |
+ |
|
+ 4txy ú |
, |
(7.27) |
||||||||
2 |
|
||||||||||||||||
|
|
|
|
ë |
|
|
|
|
|
û |
|
|
|||||
|
|
|
|
1 |
é |
|
|
|
|
|
|
ù |
|
|
|||
|
|
|
|
|
(sx |
- s y ) |
2 |
2 |
|
|
|||||||
smin = s2 |
= |
|
|
êsx + s y |
- |
|
+ 4txy ú |
, |
(7.28) |
||||||||
|
2 |
|
|||||||||||||||
|
|
|
|
ë |
|
|
|
|
|
û |
|
|
|||||
поскольку и те, и другие обозначают произвольные оси декартовых координат.
Площадки сдвига
Поскольку максимум синуса угла равен единице и достигается при уг-
- 75 -
ле 90°, из формулы (7.19) видно, что при повороте на угол 45° от главных пло-
щадок касательные напряжения принимают наибольшее по модулю значение
t max = σ1 − σ2 . (7.29) 2
Заметим, что знак касательного напряжения указывает только на его направ- ление относительно осей.
Подставив в (7.29) значения σ1 и σ2 из (7.27), (7.28), получим
|
|
|
|
1 |
|
|
|
t |
|
max |
= |
|
(sx - s y )2 + 4t2xy |
(7.30) |
|
|
|||||||
|
2 |
||||||
|
|
|
|
|
|
Площадки с наибольшими значениями касательных напряжений называ- ются площадками сдвига.
Вычислим значения нормальных напряжений на площадках сдвига, подста- вив в формулы (7.17), (7.18) α = 45°. Учитывая, что σ1 + σ2 = σx + σy , получим
|
æ |
|
|
|
ö 2 |
|
æ |
|
|
ö |
2 |
s |
|
+ s |
|
|
|
|
||
|
2 |
|
|
2 |
x |
y |
|
|
|
|||||||||||
sξ = s1 |
ç |
|
÷ |
+ s2 |
ç |
÷ |
= |
|
|
, |
(7.31) |
|||||||||
2 |
|
|
|
|
|
2 |
|
|||||||||||||
|
è |
|
ø |
|
è |
2 ø |
|
|
|
|
|
|
|
|||||||
|
æ |
|
|
|
ö 2 |
|
æ |
|
|
ö |
2 |
s |
|
+ s |
|
|
|
|
||
|
2 |
|
|
2 |
x |
y |
|
|
||||||||||||
sη = s1 |
ç |
|
|
÷ |
+ s2 |
ç |
|
÷ |
= |
|
|
. |
(7.32) |
|||||||
2 |
|
|
|
|
|
|
|
2 |
|
|||||||||||
|
è |
|
ø |
|
è |
2 ø |
|
|
|
|
|
|
|
|||||||
Значит на площадках сдвига нормальные напряжения равны между собой и равны среднему арифметическому их значений на любой паре координатных пло- щадок.
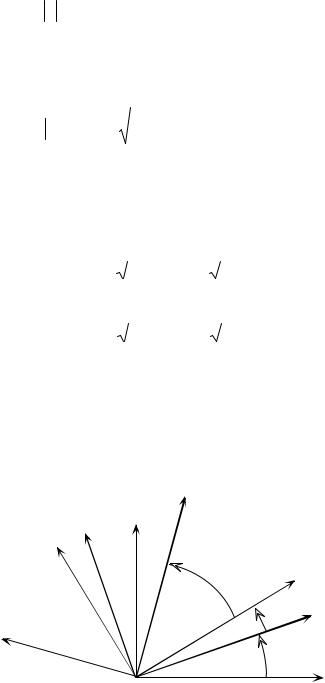
В заключение вспомним еще раз основные свойства напряжений при пло- ском напряженном состоянии вблизи точки при повороте осей координат.
x2 |
|
|
|
|
|
xсд |
Оказалось, что по напряжениям |
|||||||
η |
|
|
y |
|
на двух исходных координатных пло- |
|||||||||
|
|
|
|
45° |
|
|
|
|
щадках |
(соответствующих, |
на- |
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
пример, осям x и y, рис. 7.6) |
можно |
|||||
|
|
|
|
|
|
aглx1 |
||||||||
yсд |
|
|
вычислить напряжения для двух лю- |
|||||||||||
|
|
|
|
|
бых других координатных площадок |
|||||||||
|
|
a |
x |
|||||||||||
|
|
|
|
|
|
|
|
(на рис. 7.6 это оси x и h, соот- |
||||||
|
|
|
|
|
|
|
|
|
|
|
ветствующие углу a поворота осей |
|||
|
|
|
0 |
|
|
|
|
x |
||||||
|
|
|
|
|
|
|
|
|
|
|
координат). Среди |
всех возможных |
||
|
|
|
Рис. 7.6 |
|||||||||||
|
|
|
площадок |
можно |
указать главные |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
площадки (и соответствующие им оси координат x1 |
и x2 ), на которых нет ка- |
|||||||||||||
сательных напряжений, но зато нормальные напряжения принимают макси- мальное и минимальное значения. На угол 45° от главных повернуты коорди- натные площадки сдвига и соответствующие им оси координат xсд и yсд .
Вернёмся к одноосному напряжённому состоянию. Изображённые
- 76 -
на рис. 7.1 площадки являются главными. На них нормальные напряжения принимают максимальное и минимальное значения, а касательные напряжения равны нулю. Под углом 45° к ним действуют наибольшие касательные напря- жения τmax = (σmax − σmin ) 2 = σmax
2 = σmax  2, так как σmin = 0 . Это площадки сдвига.
2, так как σmin = 0 . Это площадки сдвига.
Некоторые частные случаи плоского напряженного состояния.
1. Напряженное состояние всестороннего растяжения-сжатия.
Допустим, что главные напряжения равны: σ1 = σ2 . Тогда из формул (7.17), (7.18) следует, что все нормальные напряжения для площадок, отличаю- щихся углом α, равны между собой:
|
σξ = σ1 cos2 α + σ1 sin2 α = σ1(cos2 α + sin2 α)= σ1 , |
|
(7.33) |
|||||
|
ση = σ1 sin2 α + σ1 cos2 α = σ1(sin2 α + cos2 α)= σ1 , |
|
(7.34) |
|||||
|
η |
σ1 |
σ1 |
|
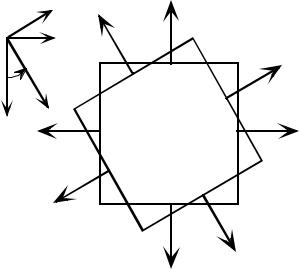
а все касательные напряжения для ука- |
|||
|
y |
|
|
|
занных площадок нулевые: |
|
||
|
|
|
|
τξη = |
σ1 − σ1 sin2α = 0. |
(7.35) |
||
α |
|
|
|
σ1 |
||||
ξ |
|
|
|
2 |
|
|
||
x |
|
|
|
Таким образом, напряженное со- |
||||
|
|
|
|
стояние |
всестороннего |
растяжения- |
||
|
σ1 |
|
|
|
||||
|
|
|
σ1 |
сжатия (при плоском напряженном со- |
||||
|
|
|
|
|
стоянии) означает равенство всех нор- |
|||
|
σ1 |
|
|
|
мальных напряжений внешнему давле- |
|||
|
|
σ1 |
|
нию на площадках, перпендикулярных |
||||
|
|
|
|
площадке |
с нулевыми |
напряжениями, |
||
|
|
|
σ1 |
|
при отсутствии касательных напряжений |
|||
Рис. 7.7 |
на тех же площадках (рис. 7.7). Вернемся |
|
|
к этому напряженному состоянию, когда будем говорить о трёхмерном случае. |
|
2. Напряженное состояние чистого сдвига.
Чистым сдвигом называется частный случай плоского напряженного состояния, при котором на одной из пар взаимно перпендикулярных площадок, проходящих через данную точку, действуют только касательные напряжения,
а нормальные напряжения равны нулю.
Выберем оси x и y так, чтобы они были перпендикулярны данным пло- щадкам (рис. 7.8). Полагая нулевыми нормальные напряжения в формулах (7.7), (7.8), (7.10), для осей, повернутых на угол α = 45° относительно осей x и y, полу-
чим
σξ = τxy sin(2 × 45°) = τxy ,
|
ση = −τxy sin(2 × 45°)= −τxy , |
- 77 - |
|
||||
|
|
(7.36) |
|||||
|
τ ξη |
= τxy cos(2 × 45°) = 0, |
|
|
|
||
откуда очевидно σmax = τmax = τxy . |
|
|
|
||||
|
Видим, что при чистом сдвиге на площадках, повернутых на угол α = 45° от- |
||||||
носительно площадок |
сдвига (площадок с максимальными касательными |
на- |
|||||
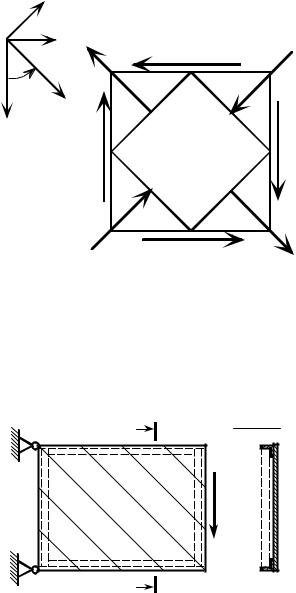
|
η |
|
|
|
|
пряжениями), действуют одни только |
|
|
y |
σξ = τxy |
τxy |
ση = −τxy |
нормальные напряжения, а касательные |
||
|
равны нулю, т.е. это главные площадки. |
||||||
45° |
|
|
|
|
|
При этом значения главных напряжений |
|
ξ |
|
|
|
|
равны и одно напряжение направлено на |
||
x |
|
|
|
|
|||
|
|
τyx |
|
|
τyx |
растяжение, а другое на сжатие. |
На- |
|
|
|
|
правления различных напряжений |
при |
||
|
|
|
|
|
|
чистом сдвиге показаны на рис. 7.8. Ка- |
|
|
|
|
|
|
|
сательные напряжения равны по модулю |
|
|
|
|
|
|
|
нормальным, следовательно, роль сдви- |
|
|
ση = −τxy |
τxy |
σξ |
= τxy |
говых деформаций и касательных |
на- |
|
|
пряжений в этом случае много более |
||||||
|
|
||||||
|
|
Рис. 7.8 |
|
|
значительна, чем при растяжении, когда |
||
|
|
|
|
|
|
касательные напряжения равны полови- |
|
не нормальных. Чистый сдвиг в материале возникает, в частности, при кручении |
|||||||
круглых стержней, что покажем позже. Поэтому по ГОСТу определение модуля уп- |
|||||||
|
|
|
|
|
ругости на сдвиг G производят именно при |
||
|
|
A |
|
A - A |
кручении круглых стержней. |
|
|
|
|
|
|
|
|
Напряженное состояние, близкое к |
|
|
|
|
|
|
чистому сдвигу, возникает в обшивке в слу- |
||
|
|
|
|
|
чае на рис. 7.9, где изображено нагружение |
||
|
|
|
|
|
тонкостенной панели силой Q, лежащей в |
||
|
|
|
|
Q |
плоскости обшивки. При достаточно боль- |
||
|
|
|
|
ших значениях нагрузки, которые зависят от |
|||
|
|
A |
|
|
параметров задачи (в частности, от толщины |
||
|
|
|
|
обшивки и размеров панели), обшивка мо- |
|||
|
|
Рис. 7.9 |
|
|
жет потерять устойчивость в направлении |
||
|
|
|
|
наибольших сжимающих напряжений. То- |
|||
|
|
|
|
|
|||
гда на её поверхности появляются волны, гребни которых направлены в направле- |
|||||||
нии действия наибольших растягивающих напряжений. Так, теория напряженного |
|||||||
состояния объясняет этот механический эффект. |
|
||||||
|
Заметим, что при чистом сдвиге площадки, на которых действуют только ка- |
||||||
сательные напряжения, являются площадками сдвига. |
|
||||||
- 78 -
Трехосное (объёмное) напряженное состояние.
D
A
 z
z
ζ
 η B
η B
y
 x ξ
x ξ
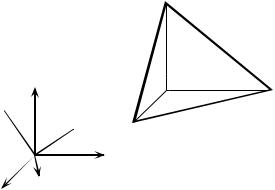
Рис. 7.10
При объёмном напряженном со- стоянии (подобно случаям однооосного и плоского НС) напряжения для произ-
вольных координатных площадок также могут быть выражены через напряжения C на исходных координатных площадках, если известны углы между осями коор- динат. Обозначим косинусы углов между осями x, y, z исходной системой коорди- нат и осями ξ, η, ζ новой системы коор-
динат, как указано в табл. 7.1. Таблица 7.1
|
Оси исходной системы координат |
||
Оси новой |
x |
y |
z |
системы ко- |
|
|
|
ординат |
|
|
|
ξ |
l11 |
l12 |
l13 |
η |
l21 |
l22 |
l23 |
ζ |
l31 |
l32 |
l33 |
Рассмотрев условия равновесия пирамиды, изображенной на рис. 7.10 (плоскость BCD перпендикулярна оси ξ), тем же путем, что и в случаях одноо- осного и плоского НС, можно получить соотношения следующего вида
σ |
ξ |
= σ |
l2 + σ |
l2 |
+ σ l2 + 2τ |
l l + 2τ |
l l |
+ 2τ |
l l |
, |
|
||
|
|
x 11 |
y 21 |
z 31 |
xy 11 21 |
|
yz 21 31 |
, |
zx 31 11 |
|
|
||
ση = ....................................................................... |
|
|
|
|
|
|
|
|
|
|
|||
σζ = ....................................................................... |
|
|
|
|
|
|
|
, |
|
|
|
||
τξη = σxl11l12 + σyl21l22 + σzl31l32 + |
|
|
|
|
|
|
|
||||||
+ τxy (l11l22 + l12l21)+ τ yz (l21l32 + l22l31 )+ τzx (l31l12 + l32l11 ) , |
(7.37) |
||||||||||||
τηζ = ....................................................................... |
|
|
|
|
|
|
|
, |
|
|
|
||
τζξ = σxl13l11 + σyl23l21 + σzl33l31 + |
|
|
|
|
|
|
|
||||||
+ τxy (l13l21 + l11l23 )+ τyz (l23l31 + l21l33 )+ τzx (l33l11 + l31l13 ) , |
|
|
|||||||||||
которые |
являются |
обобщением |
формул |
(7.7, |
7.8, |
7.10). |
Поскольку |
sin α = |
|||||
= cos(90° − α) , то структура соотношений (7.7, 7.8, 7.10) и (7.37) совпадает. Ин- тересно отметить, что если вернуться к единообразным обозначениям для каса- тельных и нормальных напряжений (6.2), учесть закон парности касательных на- пряжений, а оси обозначать соответственно номерами 1, 2, 3 и 1', 2', 3', то равенст-

- 79 -
ва (7.37) можно записать в следующей лаконичной форме:
3 |
3 |
|
σm'n' = å åσik lmilnk (m,n = 1, 2, 3). |
(7.38) |
|
i=1 k =1 |
|
|
В трехмерном случае, как и при плоском напряженном состоянии, суще-
ствуют главные площадки с нулевыми касательными напряжениями и главные нормальные напряжения на этих площадках:
σ1 = σmax > σ2 > σ3 = σmin . |
(7.39) |
Сумма нормальных напряжений на координатных площадках вблизи данной точки не зависит от выбора координатных осей:
σ1 + σ2 + σ3 = σx + σ y + σz = σξ + ση + σζ = const . |
(7.40) |
Экстремальные значения касательных напряжений выражаются через главные напряжения по формулам, аналогичным формуле для плоского на-
пряженного состояния
τ12 = (σ1 − σ2 ) 2; τ23 = (σ2 − σ3 ) 2; τ13 = τmax = (σ1 − σ3 ) 2 , |
(7.41) |
однако площадок сдвига в том виде, в каком они существуют в плоском случае, в трехмерном случае нет. Вывода этих соотношений не приводим и подробнее дан- ный вопрос не рассматриваем, поскольку в курсе сопротивления материалов ре- шаются в основном задачи для одноосного и плоского напряженных состояний.
Отметим отдельно, что в трехмерном случае также существует напря- женное состояние всестороннего растяжения-сжатия. Нормальные напряжения на всех площадках внутри тела в этом случае оказываются одинаковыми и рав- ными приложенному внешнему давлению. Касательных же напряжений в теле в этом случае нет совсем. Вследствие этого сплошные пластичные метал- лические тела при сжатии вообще не разрушаются и даже не испытывают пла- стических деформаций. В данном случае твердое тело ведёт себя в точности так же, как и жидкость, передавая приложенное внешнее давление по всем на- правлениям без изменения. Пластические деформации и разрушение, как видно из этого факта, при сжатии происходят вследствие сдвиговых деформаций.
Понятие тензора напряжений
Вспомним сначала, что такое вектор. Наиболее часто вектор определяют как направленный отрезок. Однако вектору можно дать и другое определение, полностью эквивалентное данному. Вектор − это величина, характеризующаяся тремя компонентами, которые меняются по известным законам при повороте системы координат. Для вектора a эти законы имеют вид
aξ = axl11 + ayl12 + azl13 ,
aη = axl21 + ayl22 + azl23 , |
(7.42) |
- 80 -
aζ = axl31 + ayl32 + azl33 ,
где lij (i, j = 1,2,3) – косинусы углов между осями координат, определяемые
табл. 7.1. Смысл этих формул прост. Все составляющие вектора в старой сис- теме координат надо проектировать на направление новой оси, и сумма проек- ций даст составляющую в новых осях.
При этом сам вектор не зависит от выбора той или иной системы ко- ординат. При любой системе координат это один и тот же объект, но его про- явление в каждой системе координат свое. Если вектор, т.е. его компоненты, известны хотя бы в одной системе координат, то он или они известны и во всех других системах координат из (7.42). Отметим, что формулы (7.42) также могут быть записаны в лаконичной форме, подобной (7.38):
3 |
|
am' = åailim , (m = 1, 2, 3). |
(7.43) |
i=1
Аналогичная ситуация и с напряжениями. Если 9 компонентов напряже- ний (из которых только 6 независимых) вблизи произвольной точки известны в некоторых осях координат, то они известны и в любой другой системе коор- динат благодаря формулам (7.37) или (7.38). Очевидно также, что напряженное состояние вблизи точки – это некоторое физическое явление, которое не за- висит от того, в какой системе координат оно рассматриваеется. От выбора системы координат зависит только проявление этого физического явления. За- метим, что формулы (7.38) явно являются некоторым обобщением формул
(7.43).
Из сказанного ясно, что напряженное состояние вблизи точки может рас- сматриваться как одна математическая величина в данной точке, имеющая 9 компонентов, которые изменяются при повороте осей координат по форму- лам (7.38). Оказывается в физике и механике существует много величин, имеющих 9 компонентов и меняющихся по закону (7.38), в нашем курсе это напряжения, деформации и моменты инерции твердого тела.
В математике изучены свойства таких величин, их называют тензорами. Точ- нее это – частный вид тензора, симметричный тензор второго ранга. Симметричный
– вследствие попарного равенства компонентов (касательных напряжений), что приводит к симметрии относительно главной диагонали матрицы (6.2). Вектор с точки зрения тензорного подхода представляет собой тензор первого ранга. Суще- ствуют тензоры третьего (27 компонентов) и более высоких рангов. К сожалению, тензоры второго и последующих рангов (в отличие от вектора) не имеют столь простого геометрического представления.
Формулы (7.38) и (7.43) и им подобные называются основным тензорным признаком. Если для некоторой многокомпонентной величины удалось доказать
